



第49讲 直线的方程 第50讲 直线的位置关系-2023届高考数学二轮复习经典结论微专题
展开通关一、直线的倾斜角
(1)定义:如下图,对于一条与轴相交的直线,如果把轴绕着交点按逆时针方向旋转到和直线重合时,所转发最小正角记为,那么就叫做直线的倾斜角.
(2)规定:当直线与轴平行或重合时,它的倾斜角为0.
(3)范围:直线的倾斜角的取值范围是.
通关二、求斜率的常用方法
(1)当倾斜角不是时,;.
(2)直线经过两点,其斜率为;
(3)方程为的直线的斜率为.
(4)常用倾斜角与斜率的对应关系:
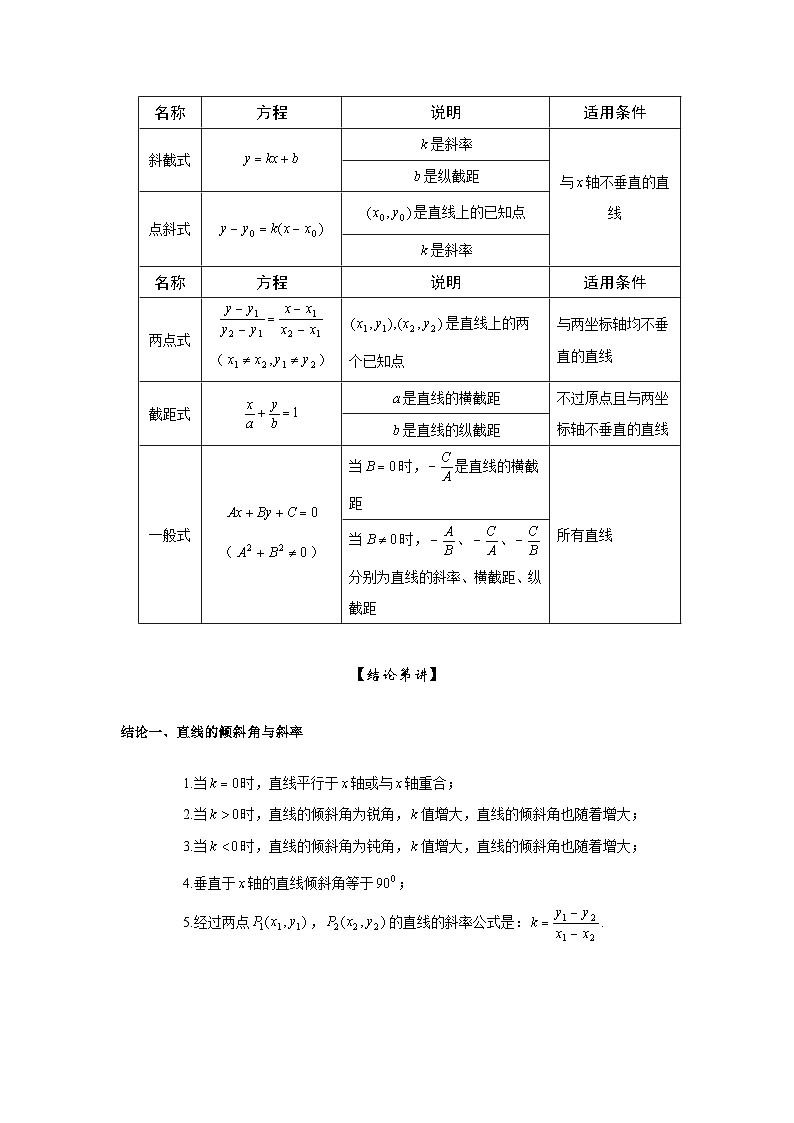
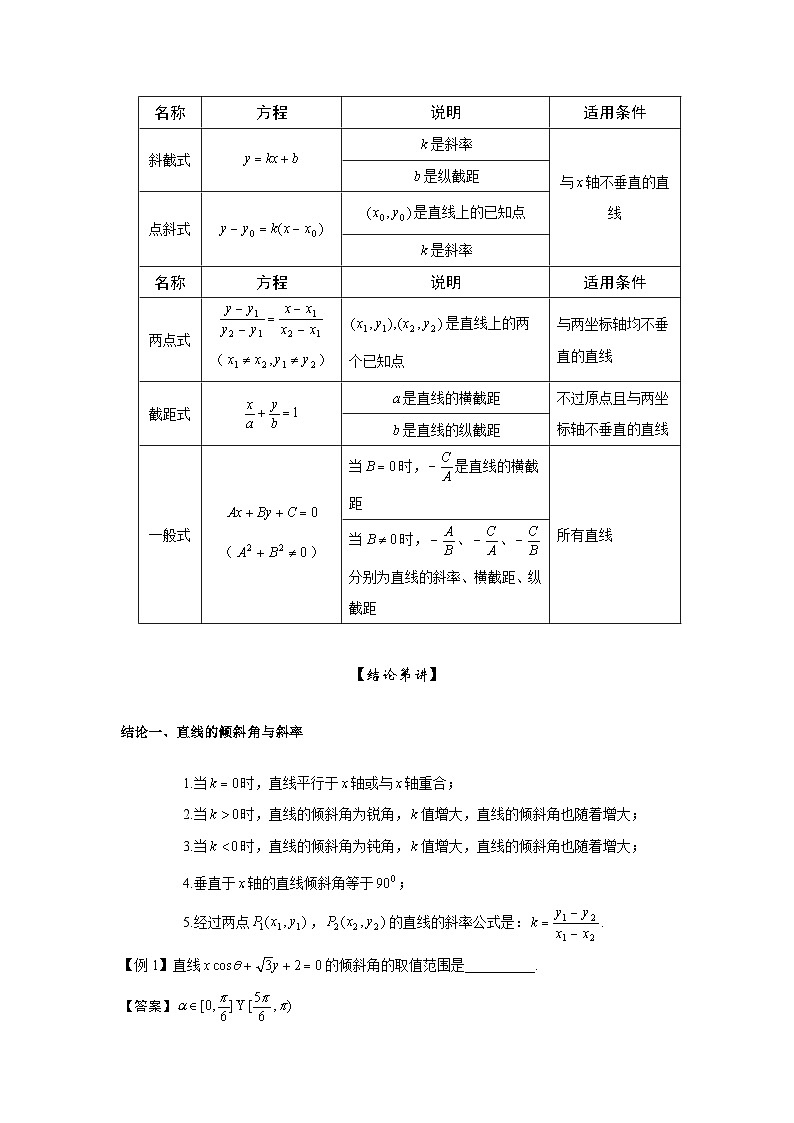
通关三、直线方程的几种形式
【结论第讲】
结论一、直线的倾斜角与斜率
1.当时,直线平行于轴或与轴重合;
2.当时,直线的倾斜角为锐角,值增大,直线的倾斜角也随着增大;
3.当时,直线的倾斜角为钝角,值增大,直线的倾斜角也随着增大;
4.垂直于轴的直线倾斜角等于;
5.经过两点,的直线的斜率公式是:.
【例1】直线的倾斜角的取值范围是__________.
【答案】
【解析】 已知直线的方程为,其斜率,记其倾斜角为,由,得,即.由,得.
【变式】 若直线经过,两点(),那么的倾斜角的取值范围是( )
A.B.
C.D.
【答案】 B
【解析】 由直线经过,两点,可利用斜率公式得.又,则倾斜角的取值范围是.故选B.
结论二、三点共线
经过两点,()的直线的斜率公式为.若点都在某条斜率存在的直线上,那么由任意两点的坐标都可以确定这条直线的斜率,即,则直线与或与的斜率相同,且又过同一点或,因此直线与或与重合.
【例2】若三点,,共线,则实数__________.
【答案】
【解析】 由题意得,.因为三点共线,所以,所以,解得.
【变式】 若三点,,在同一直线上,则的关系是__________.
【答案】
【解析】 由三点共线知,化简得应满足.
结论三、直线过定点模型
过定点的直线系方程:,还可以表示为(斜率不存在时可设).
【例3】 设,过定点的动直线和过定点的动直线交于点,则的最大值是__________.
【答案】5
【解析】 由题意可知,动直线经过定点,动直线即
m(x-1)-y+3=0,经过定点B(1,3).注意到动直线x+my=0和动直线mx-y-m+3=0始终垂直,P又是两条直线的交点,则有PAPB,所以=10.故 (当且仅当|PA|=|PB|=时取等号)
【变式】 已知点A(2,-3),B(-3,-2),直线l的方程为kx-y-k+1=0,且与线段AB相交,则直线l的斜率k的取值范围为( )
A. 或B.或 C.D.
【答案】 A.
【解析】因为直线l的方程kx-y-k+1=0可化为k(x-1)-(y-1)=0,所以直线l过定点P(1,1),如图所示.又直线PA的斜率 = =-4,直线PB的斜率 ==,所以当直线l与线段AB相交时,直线l的斜率k的取值范围是k 或k -4.故选A.
第50讲 直线的位置关系
通关一、两条直线的位置关系
通关二、两条直线的交点
对于直线它们的交点通过方程组 求解
(1)方程组有唯一解,交点坐标就是方程组的解;
(2)方程组无解 平行;
(3)方程组有无数解 重合
通关三、点线对称问题
(1)求已知点关于点的对称点: 关于点 的对称点为.
(2)点关于直线的对称点: 两直线连线与已知直线斜率之积等于-1,②两点的中点在已知直线上.
(3)直线关于某点对称的问题:直线关于点的对称问题,可转化为直线上的点关于某点对称的问题,这里需要注意到的是两对称直线是平行的,我们往往利用平行直线系去求解.
(4)直线关于直线的对称问题:直线关于直线的对称问题,包含有两种情形:①两直线平行②两直线相交。对于①,我们可以转化为点关于直线的对称问题去求解;对于②,其一般解法为先求交点,再用“到角”,或是转换为点关于直线的对称问题.
(5)两点关于点对称、两点关于直线对称的常见结论:
①点(x,y)关于x轴的对称点为(x,-y);
②点(x,y)关于y轴的对称点为(-x,y);
③点(x,y)关于原点的对称点为(-x,-y);
④点(x,y)关于直线x-y=0的对称点为(y,x);
⑤点(x,y)关于直线x+y=0的对称点为(-y,-x).
结论一、直线的平行
设直线 ,则 且,平行于直线的直线系方程为
【例1】若直线x+(1+m)y-2+m=0与直线2mx+4y+9=0平行,则m的值为_____
【答案】 1或-2
【解析】 因为两直线平行,所以,所以,即m=1或m=-2
【变式】 已知是直线上的一点是直线外一点,则方程 表示的直线与直线 的位置关系是( )
A 平行 B 重合C 垂直D 斜交
【答案】A
【解析】是直线 上的一点,故有 , 是直线外一点,故有,是一个实数,从而表示的直线与直线平行且不重合.故选A.
结论二、直线的垂直
设直线,,则 ,垂直于直线 的直线系方程为:
【例2】已知直线 ,,若 ,则实数a的值是______
【答案】-3或0
【解析】 若,,且,则,解得 或
【变式】 直线过点(-1,2)且与直线垂直,则的方程是( )
A. B.
C. D.
【答案】 A
【解析】 解法一 由题意可得的斜率为,所以,即 .故选A.
解法二 由题意可设的方程为 ,把点(-1,2)带入直线的方程得,所以C=-1,即.故选A.
结论三、直线系方程
经过两条已知直线,的交点的直线系方程为:(不包括直线)
【例3】直线经过直线3x+2y+6=0和2x+5y-7=0的交点,且在两坐标轴上的截距相等,则直线的方程为_____
【答案】3x+4y=0及x+y+1=0
【解析】设所求的直线为,即.由题意知:,,它在x轴,y轴上的截距分别为依题意有或,解得,将其带入所设方程,得及.
【变式】已知直线经过直线2x-y-3=0和4x-3y-5=0的交点P,且垂直于直线2x+3y+5=0,则直线的方程为_____.
【答案】3x-2y-4=0
【解析】直线的方程可设为 (其中为常数),即.因为直线与直线垂直,所以,解得=1.故直线的方程为
结论四、两点间的距离公式
平面上任意两点A(,),B(,)间的距离公式为
【例4】函数,则y的取值范围为_____
【答案】(-1,1)
【解析】设,,为平面内三点,则,.因为,且,所以,即.函数的值域为.
【变式】 已知函数,则的最小值为_____
【答案】
【解析】将函数表达式变形为:可以看作到点与到点的距离之和,即在x轴上求一点P,使最小.由右图可知,可转化为求两点A'(1,-1)和B(2,2)间的距离,其距离为函数f(x)的最小值.所以f(x)的最小值为
结论五、点到直线的距离公式
点到直线的距离
【例5】 已知直线,两点,若且,则( )
A.直线l与直线 不相交
B.直线l与线段 的延长线相交
C.直线l与线段 的延长线相交
D.直线l与线段 相交
【答案】C
【解析】与同号,即和在直线的同侧,如图所示.而,即到的距离大于到的距离,显然,与线段的延长线相交.故选C.
【变式】我们知道: 在平面内,点到直线Ax+By+C=0的距离公式为 .通过类比的方法,可求得在空间中,点(2,4,1)到平面x+2y+2z+3=0的距离为( )
A.3B.5C. D.
【答案】B
【解析】因为在平面内,点到直线的距离公式为,类比可得:点(2,4,1)到平面x+2y+2z+3=0的距离为.故选B
结论六、两平行直线间的距离公式
两条平行直线与间的距离
【例】6 已知直线:x+y+1=0, :x+y-1=0,则,之间的距离为( )
A.1B. C. D.2
【答案】 B
【解析】 在上任取一点(-1,0),两条平行线间的距离就等于点(-1,0)到直线的距离,为 .故选B.
【变式】 已知直线,,若,则与的距离为_____
【答案】
【解析】直线,当 时,,解得.当a=1时, 与重合,不满足题意;当a=-1时, ,此时则与的距离为.
结论七、中心对称
中点坐标公式:,点为点与的中点.
点关于的对称点为.直线关于点的对称问题可以转化为点关于点的对称问题.
【例7】若直线与直线关于点(2,1)对称,则直线恒过定点( )
A.(0,4)B.(0,2)C.(-2,4)D.(4,-2)
【答案】B
【解析】 设上任意一点坐标为,则关于的对称点为,又因为此点在上,则,即,所以直线恒过定点.故选B.
【变式】 若圆C的半径为1,其圆心与点(1,0)关于点(0,2)对称,则圆C的标准方程为_____
【答案】
【解析】 因为点(1,0)关于点(0,2)对称的点的坐标为(-1,4),所以所求圆的圆心为(-1,4),半径为1,于是圆C的标准方程为
结论八、轴对称
点P(a,b)关于直线的对称点为P'(m,n),则有.直线与直线的对称问题可转化为点与直线的对称问题.
【例8】点A(2,-3)关于直线的对称点为( )
A.(3,-2)B.(4,-1)C.(5,0)D.(3,1)
【答案】 B
【解析】 设点A(2,-3)关于直线的对称点为P(a,b),则 = =1,所以a-b=5① ,又线段AP的中点( , )在直线上,即 ,整理得②,联立①②解得a=4,b=-1,所以点A(2,-3)关于直线的对称点P点的坐标为(4,-1).故选B.
【变式】 点(3,-1)关于直线x+y=0的对称点为_____
【答案】 (1,-3)
【解析】 设点(3,-1)关于直线x+y=0的对称点为(a,b),则 ,解得,所以点(3,-1)关于直线x+y=0的对称点为(1,-3)
倾斜角
斜率
1
名称
方程
说明
适用条件
斜截式
是斜率
与轴不垂直的直线
是纵截距
点斜式
是直线上的已知点
是斜率
名称
方程
说明
适用条件
两点式
()
是直线上的两个已知点
与两坐标轴均不垂直的直线
截距式
是直线的横截距
不过原点且与两坐标轴不垂直的直线
是直线的纵截距
一般式
()
当时,是直线的横截距
所有直线
当时,、、分别为直线的斜率、横截距、纵截距
斜截式
一般式
方程
相交
垂直
平行
且
或
重合
且
第52讲 直线与圆的位置关系-2023届高考数学二轮复习经典结论微专题: 这是一份第52讲 直线与圆的位置关系-2023届高考数学二轮复习经典结论微专题,文件包含第52讲直线与圆的位置关系-解析版docx、第52讲直线与圆的位置关系-原卷版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
第59讲 统计-2023届高考数学二轮复习经典结论微专题: 这是一份第59讲 统计-2023届高考数学二轮复习经典结论微专题,文件包含第59讲统计-解析版docx、第59讲统计-原卷版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
第56讲 直线与圆锥曲线-2023届高考数学二轮复习经典结论微专题: 这是一份第56讲 直线与圆锥曲线-2023届高考数学二轮复习经典结论微专题,文件包含第56讲直线与圆锥曲线-解析版docx、第56讲直线与圆锥曲线-原卷版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。












