专题16 锐角三角函数及其应用（5大考点）-中考数学总复习真题探究与变式训练（全国通用）

这是一份专题16 锐角三角函数及其应用（5大考点）-中考数学总复习真题探究与变式训练（全国通用），文件包含专题16锐角三角函数及其应用5大考点解析版docx、专题16锐角三角函数及其应用5大考点原卷版docx等2份试卷配套教学资源，其中试卷共103页， 欢迎下载使用。

第四部分 三角形
专题16 锐角三角函数及其应用（5大考点）
核心考点
核心考点一 特殊角的三角函数值及其计算
核心考点二 由三角函数值求锐角
核心考点三 锐角三角函数的增减性
核心考点四 解直角三角形及其应用
核心考点五 三角函数的综合
新题速递

核心考点一 特殊角的三角函数值及其运算

例1 （2021·贵州黔东南·统考中考真题）如图，在边长为2的正方形ABCD中，若将AB绕点A逆时针旋转，使点B落在点的位置，连接B，过点D作DE⊥，交的延长线于点E，则的长为（   ）

A． B． C． D．
【答案】A
【分析】利用已知条件求得,设，将都表示出含有的代数式，利用的函数值求得，继而求得的值
【详解】
设交于点,
由题意：
是等边三角形

四边形为正方形

∴∠CBF=90°-60°=30°，
DE⊥

又

设
则






解得：

故选A
【点睛】本题考查了正方形的性质，等边三角形的判定与性质，锐角三角函数定义，特殊角的锐角三角函数值，灵活运用锐角三角函数的定义及特殊三角函数值是解题的关键．
例2 ．（2022·黑龙江绥化·统考中考真题）定义一种运算；，．例如：当，时，，则的值为_______．
【答案】
【分析】根据代入进行计算即可．
【详解】解：
=
=
=
=．
故答案为：．
【点睛】此题考查了公式的变化，以及锐角三角函数值的计算，掌握公式的转化是解题的关键．
例3 （2022·山东潍坊·中考真题）（1）在计算时，小亮的计算过程如下：
解：



小莹发现小亮的计算有误，帮助小亮找出了3个错误．请你找出其他错误，参照①～③的格式写在横线上，并依次标注序号：
①；②；③；
____________________________________________________________________________．
请写出正确的计算过程．
（2）先化简，再求值：，其中x是方程的根．
【答案】（1）④tan30°=；⑤(-2)-2=，⑥(-2)0=1；28；（2），．
【分析】（1）根据乘方、绝对值、特殊角的三角函数值、立方根、负整数指数幂、零指数幂的法则计算即可；
（2）先把括号内通分，接着约分得到原式=，然后利用因式分解法解方程x2-2x-3=0得到x1=3，x2=-1，则利用分式有意义的条件把x=-1代入计算即可．
【详解】（1）其他错误，有：④tan30°=；⑤(-2)-2=，⑥(-2)0=1，
正确的计算过程：
解：


=28；
（2）


=，
∵x2-2x-3=0，
∴（x-3）（x+1）=0，
x-3=0或x+1=0，
∴x1=3，x2=-1，
∵x=3分式没有意义，
∴x的值为-1，
当x=-1时，原式==．
【点睛】本题考查了实数的运算，解一元二次方程---因式分解法，分式的化简求值．也考查了特殊角的三角函数值、立方根、负整数指数幂、零指数幂．


知识点：特殊角的三角函数值
1. 图表记忆
三角函数

图形记忆
30°
45°
60°











1


2. 规律记忆
30°，45°，60°角的正弦值的分母都是2，分子依次为1，，；
30°，45°，60°角的余弦值分别是60°，45°，30°角的正弦值。




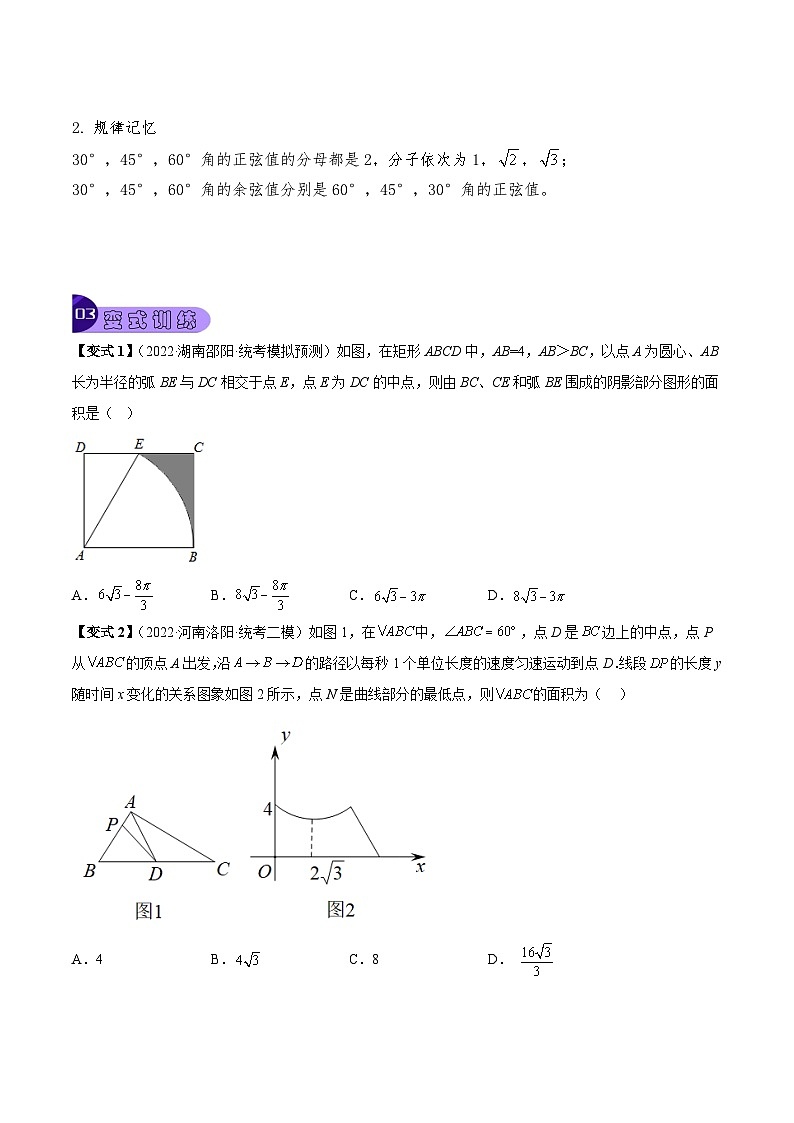
【变式1】（2022·湖南邵阳·统考模拟预测）如图，在矩形ABCD中，AB=4，AB＞BC，以点A为圆心、AB长为半径的弧BE与DC相交于点E，点E为DC的中点，则由BC、CE和弧BE围成的阴影部分图形的面积是（   ）

A． B． C． D．
【答案】A
【分析】根据矩形的性质得出AB=CD=AE=4，∠ADC=90°，结合中点及特殊角的三角函数值与勾股定理得出∠DAE=30°，AD=，∠BAE=60°，结合图形得出，代入求解即可．
【详解】解：∵四边形ABCD为矩形，
∴AB=CD=AE=4，∠ADC=90°
∵E为CD中点，
∴CE=DE=2，
在Rt∆ADE中，
，
∴∠DAE=30°，AD=，
∴∠BAE=60°，



，
故选：A．
【点睛】题目主要考查矩形的性质，特殊角的三角形函数值，勾股定理，求不规则图形的面积等，理解题意，综合运用这些知识点是解题关键．
【变式2】（2022·河南洛阳·统考二模）如图1，在中，，点D是边上的中点，点P从的顶点A出发，沿的路径以每秒1个单位长度的速度匀速运动到点D．线段的长度y随时间x变化的关系图象如图2所示，点N是曲线部分的最低点，则的面积为（    ）

A．4 B． C．8 D．
【答案】D
【分析】由函数图象可知AD=4，当DP⊥AB时，AP=,此时有DP长的最小值，由勾股定理可以求出DP的长度，进而结合∠B=60°求得BP，即可求出△ABD的面积，然后利用点D是边上的中点，得到．
【详解】解：过D作DP⊥AB于P

由函数图像可得，AD=4，当DP⊥AB时，AP=,此时有DP长的最小值，
∴
∵
∴
∴
∴
∵点D是边上的中点，
∴
故选：D
【点睛】本题考查了垂线段最短、勾股定理、特殊角度的三角函数值，解题的关键是通过函数图象得到当DP⊥AB时，AP=．
【变式3】（2020·四川自贡·校考一模）在中，若，，都是锐角，则是______三角形．
【答案】等边
【分析】根据非负数的性质分别求出∠A和∠B，继而可判断的形状．
【详解】解：∵，
∴，，
∴，，
∴∠A=60°，∠B=60°，
∴是等边三角形．
故答案为：等边．
【点睛】本题考查特殊角的三角函数值，非负数的性质，等边三角形的判断，解题关键是熟记特殊角的三角函数值．
【变式4】（2022·贵州铜仁·统考二模）如图，将一个矩形纸片OABC放置在平面直角坐标系中，点O(0，0)，点B(，2)．D是边BC上一点(不与点B重合)，过点D作DE∥OB交OC于点E．将该纸片沿DE折叠，得点C的对应点C′．当点C′落在OB上时，点C′的坐标为________．

【答案】
【分析】根据B点坐标可求出AB、OB，得到，所以，，再利用折叠与平行的性质，证明△OEC′是等边三角形，OE=CD=，然后可利用三角函数求出点C′的坐标．
【详解】∵点B坐标为(，2)，
∴AB=2，OA=，
∴
∴
∴，
∵C′是C关于DE的对称点
∴， EC=EC′
∵DE∥OB
∴=60°
∴∠OE C′=180°-2×60°=60°
∴△OE C′是等边三角形
∴OE= EC=EC′==
∴C′横坐标=，纵坐标=
∴C′坐标为
【点睛】本题考查了三角形，熟练运用特殊三角形的性质是解题的关键．
【变式5】．（2021·新疆乌鲁木齐·校考三模）计算：
【答案】6
【分析】利用有理数的乘方法则，绝对值的意义，特殊角的三角函数值，零指数幂的意义化简计算即可．
【详解】解：原式=
=
=6
【点睛】本题主要考查了实数的运算，有理数的乘方法则，绝对值的意义，特殊角的三角函数值，零指数幂的意义，正确使用上述法则进行运算是解题的关键．

核心考点二 由三角函数值求锐角

例1 （2021·山东泰安·统考中考真题）如图，在中，，以点A为圆心，3为半径的圆与边相切于点D，与，分别交于点E和点G，点F是优弧上一点，，则的度数是（   ）

A．50° B．48° C．45° D．36°
【答案】B
【分析】连接AD，由切线性质可得∠ADB=∠ADC=90°，根据AB=2AD及锐角的三角函数可求得∠BAD=60°，易求得∠ADE=72°，由AD=AE可求得∠DAE=36°，则∠GAC=96°，根据圆周角定理即可求得∠GFE的度数．
【详解】解：连接AD，则AD=AG=3，
∵BC与圆A相切于点D，
∴∠ADB=∠ADC=90°，
在Rt△ADB中，AB=6，则cos∠BAD==，
∴∠BAD=60°，
∵∠CDE=18°，
∴∠ADE=90°﹣18°=72°，
∵AD=AE，
∴∠ADE=∠AED=72°，
∴∠DAE=180°﹣2×72°=36°，
∴∠GAC=36°+60°=96°，
∴∠GFE=∠GAC=48°，
故选：B．

【点睛】本题考查切线性质、锐角的三角函数、等腰三角形的性质、三角形的内角和定理、圆周角定理，熟练掌握切线性质和圆周角定理，利用特殊角的三角函数值求得∠BAD=60°是解答的关键．
例2 ．（2022·重庆·统考中考真题）如图，在矩形中，，，以B为圆心，的长为半径画弧，交于点E．则图中阴影部分的面积为_________．（结果保留）

【答案】
【分析】先根据特殊角的锐角三角函数值，求出，进而求出，再根据扇形的面积公式求解即可．
【详解】解：∵矩形，
，
以B为圆心，的长为半轻画弧，交于点E， ，
，
在中，，
，
，
，
S阴影 ．
故答案为： ．
【点睛】本题考查了由特殊角的三角函数值求角度数，矩形的性质，扇形的面积的计算，综合掌握以上知识点并熟练运用是解题的关键．
例3 （2021·山东菏泽·统考中考真题）在矩形中，，点，分别是边、上的动点，且，连接，将矩形沿折叠，点落在点处，点落在点处．

（1）如图1，当与线段交于点时，求证：；
（2）如图2，当点在线段的延长线上时，交于点，求证：点在线段的垂直平分线上；
（3）当时，在点由点移动到中点的过程中，计算出点运动的路线长．
【答案】（1）见解析；（2）见解析；（3）．
【分析】（1）分别根据平行线的性质及折叠的性质即可证得∠DEF＝∠EFB，∠DEF＝∠HEF，由此等量代换可得∠HEF＝∠EFB，进而可得PE＝PF；
（2）连接PM，ME，MF，先证RtPHM≌RtPBM（HL），可得∠EPM＝∠FPM，再证EPM≌FPM（SAS），由此即可得证；
（3）连接AC，交EF于点O，连接OG，先证明EAO≌FCO（AAS），由此可得OC＝AC＝5，进而根据折叠可得OG＝OC＝5，由此得到点G的运动轨迹为圆弧，再分别找到点G的起始点和终点便能求得答案．
【详解】（1）证明：∵在矩形ABCD中，
∴ADBC，AB＝CD；
∴∠DEF＝∠EFB，
∵折叠，
∴∠DEF＝∠HEF，
∴∠HEF＝∠EFB，
∴PE＝PF；
（2）证明：连接PM，ME，MF，


∵在矩形ABCD中，
∴AD＝BC，∠D＝∠ABC＝∠PBA＝90°，
又∵AE＝CF，
∴AD－AE＝BC－CF，
即：DE＝BF，
∵折叠，
∴DE＝HE，∠D＝∠EHM＝∠PHM＝90°，
∴BF＝HE，∠PBA＝∠PHM＝90°，
又∵由（1）得：PE＝PF，
∴PE－HE＝PF－BF，
即：PH＝PB，
在RtPHM与RtPBM中，
，
∴RtPHM≌RtPBM（HL），
∴∠EPM＝∠FPM，
在EPM与FPM中，
，
∴EPM≌FPM（SAS），
∴ME＝MF，
∴点M在线段EF的垂直平分线上；
（3）解：如图，连接AC，交EF于点O，连接OG，

∵AB＝CD＝5，，
∴BC＝，
∴在RtABC中，AC＝＝，
∵ADBC，
∴∠EAO＝∠FCO，
在EAO与FCO中，
，
∴EAO≌FCO（AAS），
∴OA＝OC＝AC＝5，
又∵折叠，
∴OG＝OC＝5，
当点E与点A重合时，如图所示，此时点F，点G均与点C重合，

当点E与AD的中点重合时，如图所示，此时点G与点B重合，

∵O为定点，OG＝5为定值，
∴点G的运动路线为以点O为圆心，5为半径的圆弧，且圆心角为∠BOC，
在RtABC中，tan∠BAC＝＝，
∴∠BAC＝60°，
∵OA＝OB＝OC＝OG，
∴点A、B、C、G在以点O为圆心，5为半径的圆上，
∴∠BOC＝2∠BAC＝120°，
∴的长为＝，
∴点运动的路线长为．
【点睛】本题考查了矩形的性质、折叠的性质、全等三角形的判定及性质、圆的相关概念及性质，弧长公式的应用，第（3）问能够发现OG＝5是解决本题的关键．


【变式1】（2022·山东滨州·统考一模）如图，在半径为6的⊙O中，点A是劣弧的中点，点D是优弧上一点，sinD=,则BC的长为（    ）

A． B． C． D．
【答案】A
【分析】设BC与OA交于E点，根据点A是劣弧的中点，得到=，继而得到∠COA=∠AOB，根据，得出锐角∠D=30°，再同一段弧其所对圆心角是其所对应圆周角的两倍，得到∠COA=2∠D，∠COA=60°=∠AOB，再得到∠OCB=∠OBC=30°，因为∠OEC=180°-∠OCB-∠COA=90°，可知△OEC是直角三角形，利用特殊角即可求出CE，再同理求出BE，即可求出BC．
【详解】设BC与OA交于E点，

∵点A是劣弧的中点，
∴=，
∴圆心角∠COA=∠AOB，
∵，
∴锐角∠D=30°，
∵同一段弧其所对圆心角是其所对应圆周角的两倍，即∠COA=2∠D，
∴∠COA=60°=∠AOB，
又∵OC=OB，
∴∠OCB=∠OBC=30°，
∴∠OEC=180°-∠OCB-∠COA=90°，即△OEC是直角三角形，
∵OC=6，∠OCB=∠OBC=30°，
∴CE=OC=，
同理可求出BE=，
∴BC=CE+EB=，
故选：A．
【点睛】本题考查了锐角三角函数、圆心角与圆周角的关系、解直角三角形等知识．依据得到∠D=30°再得到∠COA=2∠D，∠COA=60°=∠AOB是解答本题的关键．
【变式2】（2022·山东·统考二模）如图，已知在矩形中，，点是边上的一个动点，连结，点关于直线的对称点为，当点运动时，点也随之运动．若点从点运动到点，则线段扫过的区域的面积是（    ）

A． B． C． D．
【答案】B
【分析】先判断出点Q在以BC为直径的圆弧上运动，再判断出点C1在以B为圆心，BC为直径的圆弧上运动，找到当点P与点A重合时，点P与点D重合时，点C1运动的位置，利用扇形的面积公式及三角形的面积公式求解即可．
【详解】解：设BP与CC1相交于Q，则∠BQC=90°，

∴当点P在线段AD运动时，点Q在以BC为直径的圆弧上运动，
延长CB到E，使BE=BC，连接EC，
∵C、C1关于PB对称，
∴∠EC1C=∠BQC=90°，
∴点C1在以B为圆心，BC为直径的圆弧上运动，
当点P与点A重合时，点C1与点E重合，
当点P与点D重合时，点C1与点F重合，

此时，，
∴∠PBC=30°，
∴∠FBP=∠PBC=30°，CQ=，BQ=，
∴∠FBE=180°-30°-30°=120°，，
线段扫过的区域的面积是．
故选：B．
【点睛】本题考查了矩形的性质、三角形中位线定理、直角三角形的性质、三角函数以及扇形面积公式等知识；熟练掌握矩形的性质和轴对称的性质是解题的关键．
【变式3】（2021·贵州遵义·统考一模）在综合实践课上，某学习小组要测量塔的高度，在测量过程中，结合图形进行了操作（如图所示）．在塔AB前的平地上选择一点C，测出塔顶的仰角为30°，从C点向塔底B走80m到达D点，测出塔顶的仰角为45°，那么塔AB的高为____________m（计算结果精确到0.1m，参考数据：，）．

【答案】109.2
【分析】在Rt△ABD中，，在Rt△ABC中，，再根据CD=BC-BD=80即可求解．
【详解】根据题意可知AB⊥BC，
∴在Rt△ABD中，，
在Rt△ABC中，，
∵∠ADB=45°，∠ACB=30°，
∴，，
∵CD=80，
∴CD=BC-BD=，
∴（m），
故塔高109.2米，
故答案为：109.2．
【点睛】本题考查了解直角三角形的应用，理解仰角的含义并熟记特殊角的三角函数值是解答本题的关键．
【变式4】．（2022·吉林长春·统考二模）如图，在平面直角坐标系中，点在第一象限，连结，过点作轴于点，，，把绕点逆时针旋转后，得到，则点的坐标为______．

【答案】
【分析】根据勾股定理可得OA，根据特殊三角比求出∠AOB=60°，可知△ABO绕点O逆时针旋转后OA的对应边OA1位于x轴上，继而可得答案．
【详解】解：∵轴于点，，，
∴，
∴，
∴把绕点逆时针旋转后，得到如下图，

∵，
∴，
∴点的坐标为，
故答案为：（-2，0）
【点睛】本题主要考查旋转变换下坐标与图形的变化，解直角三角形得出OA的长是解题的根本，根据△ABO绕点O逆时针旋转120°后OA的对应边OA1位于x轴上是解题的关键．
【变式5】（2022·重庆·重庆八中校考模拟预测）如图，一艘渔船位于小岛的北偏东方向，距离小岛千米的点处，它沿着点的南偏东的方向航行．

(1)渔船航行多远距离小岛最近（结果保留根号）？
(2)渔船到达距离小岛最近点后，按原航向继续航行千米到点C处时突然发生事故，渔船马上向小岛上的救援队求救，问救援队从处出发沿着哪个方向航行到达事故地点航程最短，最短航程是多少．（结果精确到1千米，参考数据）
【答案】(1)；
(2)从处沿南偏东出发，最短行程．

【分析】（1）过点作的垂线交于点，则为所求，根据已知条件得到即可解答；
（2）根据特殊角的锐角三角函数值得到，从而求出的长度，再求出的度数，即可得到的度数．
【详解】（1）解：过点作的垂线交于点，
∵垂线段最短，上的点距离点最近，即为所求，
由题意可知：，，
∴，
∴渔船航行时，距离小岛最近．

（2）解：在中，，
，，
，
∵，，
，
．
答：从处沿南偏东出发，最短行程．
【点睛】本题考查了解直角三角形的应用中的方向角问题，结合航海中的实际问题，将解直角三角形的相关知识有机结合，体现了数学应用于实际生活的思想．


核心考点三 锐角三角函数的增减性

例1 （2020·湖南娄底·中考真题）如图，撬钉子的工具是一个杠杆，动力臂，阻力臂，如果动力F的用力方向始终保持竖直向下，当阻力不变时，则杠杆向下运动时的动力变化情况是（    ）

A．越来越小 B．不变 C．越来越大 D．无法确定
【答案】A
【分析】根据杠杆原理及的值随着的减小而增大结合反比例函数的增减性即可求得答案．
【详解】解：∵动力×动力臂=阻力×阻力臂，
∴当阻力及阻力臂不变时，动力×动力臂为定值，且定值＞0，
∴动力随着动力臂的增大而减小，
∵杠杆向下运动时的度数越来越小，此时的值越来越大，
又∵动力臂，
∴此时动力臂也越来越大，
∴此时的动力越来越小，
故选：A．
【点睛】本题主要考查了杠杆原理以及锐角三角函数和反比例函数的增减性，熟练掌握相关知识是解决本题的关键．
例2 （2022·陕西西安·交大附中分校校考三模）如图，在矩形ABCD 中，O是对角线AC的中点，E为AD上一点，若，则AB的最大值为__________．

【答案】4
【分析】设，则，根据，，根据正弦的增减性可得，当最大值，取得最大值，进而即可求解．
【详解】设，则，
则
过点，则
，当点与点重合时，取得最大值，此时最大，则最大，即取得最大值，
此时，

的最大值为
故答案为：4
【点睛】本题考查了矩形的性质，正弦的增减性，掌握三角函数的关系，矩形的性质是解题的关键．
例3 （2021·浙江宁波·统考一模）如图是某公园的一台滑梯，滑梯着地点B与梯架之间的距离．

（1）现在某一时刻测得身高1.8m的小明爸爸在阳光下的影长为0.9m，滑梯最高处A在阳光下的影长为1m，求滑梯的高；
（2）若规定滑梯的倾斜角（）不超过30°属于安全范围，请通过计算说明这架滑梯的倾斜角是否符合安全要求？
【答案】（1）2米；（2）符合
【分析】（1）利用影长物高成比例求解即可；
（2）先求出锐角三角函数值，再利用锐角三角函数值求出角的范围即可．
【详解】解：（1），
，
答：滑梯高为2米；
（2）∵AC=2m,BC=4m，
∴，
∵正切值随着角的增大函数值增大，
，
这架滑梯的倾斜角符合安全要求．
【点睛】本题考查影长物高成比例性质，正切三角函数的定义，及正切函数的增减性，掌握影长物高成比例性质，正切三角函数的定义，及正切函数的增减性是解题关键．

1. 三角函数值的变化规律
①当角度A在0°—90°间变化时，正弦值和正切值随着角度的增大（或减小）而增大（或减小）
②当角度A在0°—90°间变化时，余弦值和余切值随着角度的增大（或减小）而减小（或增大）。




【变式1】（2020·甘肃张掖·统考模拟预测）若，则下列说法不正确的是（   ）
A．随的增大而增大 B．cos随的减小而减小 C．tan随的增大而增大 D．0 【答案】B
【分析】如图，作半径为的，均为直径， 都在上，利用锐角三角函数的定义分析可得答案．
【详解】解：如图，作半径为的，均为直径，
都在上，

由
显然，＜，而＜，
所以当时，随的增大而增大，故A正确；

同理可得：
当时，cos随的减小而增大，故B错误；
当时，tan随的增大而增大，故C正确；
当，当点逐渐向移动，边逐渐接近，
逐渐接近
当时，0 故选B．
【点睛】本题考查的是锐角的正弦，余弦，正切的增减性，掌握利用辅助圆理解锐角三角函数的增减性是解题的关键．
【变式2】．（2022·上海·校考模拟预测）如果锐角A的度数是25°，那么下列结论中正确的是（    ）
A． B．
C． D．
【答案】A
【分析】根据“正弦值随着角度的增大而增大”解答即可．
【详解】解：∵0°＜25°＜30°
∴
∴．
故选A．
【点睛】本题主要考查了锐角三角形的增减性，当角度在0°~90°间变化时，①正弦值随着角度的增大（或减小）而增大（或减小）；②余弦值随着角度的增大（或减小）而减小（或增大）；③正切值随着角度的增大（或减小）而增大（或减小）．
【变式3】（2020·内蒙古·统考二模）在直角三角形ABC中，角C为直角，锐角A的余弦函数定义为_____，写出sin70º、cos40º、cos50º的大小关系__________．
【答案】          sin70º＞cos40 º＞cos50 º
【分析】根据余弦的定义即可确定答案；根据sin70°=cos20°且正弦随角度的增大而增大，余弦随角度的增大而减小即可确定大小关系．
【详解】解：∵直角三角形ABC中，角C为直角
∴BC为斜边，AC为直角边且为∠A的一边
∴余弦的定义为；
∵sin70°=cos20°且正弦在锐角范围内随角度的增大而增大，余弦在锐角范围内随角度的增大而减小
∴sin70º==cos20 º＞cos40º，cos40 º＞cos50 º
∴sin70º＞cos40 º＞cos50 º．
故答案为，sin70º＞cos40 º＞cos50 º．
【点睛】本题考查了余弦函数的定义和正弦、余弦函数的增减性，掌握正弦在锐角范围内为增函数
、余弦在锐角范围内为减函数是解答本题的关键．
【变式4】（2022·江苏宿迁·统考二模）如图，在平面直角坐标系中，点，点平分，，点、分别在、上运动，且，连接、交于点，点，连接，则度数的最大值为__________．

【答案】30°##30度
【分析】根据已知条件证明，，求得点的轨迹，延长交轴于点，以为圆心，为半径作圆，交轴于点，连接，过点，交的延长线于点，连接，根据正弦的增减性判断当与相切时候，度数最大．
【详解】点，点平分，，
，
，
，
在中，，
，
，
是等边三角形，
，
在与中，
，
，
，
，
，
，
延长交轴于点，以为圆心，为半径作圆，交轴于点，连接，过点Q作，交的延长线于点，连接，如图，

，
设直线的解析式为，
则，
解的，
，
，
，
，
优弧，
，
在上，
设，则，
为定值，随着的增大而增大，即最大时，最大，
当取得最大值，
此时与相切，
，
即度数的最大值为．
故答案为：．
【点睛】本题考查了等边三角形的性质，圆周角定理，切线的性质，正弦的增减性，求得点的轨迹是解题的关键．
【变式5】（2022春·全国·九年级专题练习）如图，已知和射线上一点（点与点不重合），且点到、的距离为、．

(1)若，，，试比较、的大小；
(2)若，，，都是锐角，且．试判断、的大小，并给出证明．
【答案】(1)
(2)，理由见解析

【分析】（1）根据三角函数的定义，分别表示出，进而根据角度比较函数值的大小即可求解；
（2）同（1）的方法，即可求解．
【详解】（1）解：在中，，
，
在中，，
，
又，
；
（2）解：由（1）得，，
，
，
．
【点睛】本题考查了正弦的定义，掌握三角函数的定义是解题的关键．

核心考点四 解直角三角形及其应用

例1 （2022·湖北黄石·统考中考真题）我国魏晋时期的数学家刘徽首创割圆术：割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体，而无所失矣"，即通过圆内接正多边形割圆，从正六边形开始，每次边数成倍增加，依次可得圆内接正十二边形，内接正二十四边形，……．边数越多割得越细，正多边形的周长就越接近圆的周长．再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率．设圆的半径为R，图1中圆内接正六边形的周长，则．再利用圆的内接正十二边形来计算圆周率则圆周率约为（    ）

A． B． C． D．
【答案】A
【分析】求出正十二边形的中心角，利用十二边形周长公式求解即可．
【详解】解：∵十二边形是正十二边形，
∴，
∵于H，又，
∴，
∴圆内接正十二边形的周长，
∴
故选：A．

【点睛】本题考查的是正多边形和圆、等腰三角形的性质，解直角三角形，求出正十二边形的周长是解题的关键．
例2 （2022·湖北黄石·统考中考真题）某校数学兴趣小组开展无人机测旗杆的活动：已知无人机的飞行高度为30m，当无人机飞行至A处时，观测旗杆顶部的俯角为30°，继续飞行20m到达B处，测得旗杆顶部的俯角为60°，则旗杆的高度约为________m．（参考数据：，结果按四舍五八保留一位小数）

【答案】12.7
【分析】设旗杆底部为点C，顶部为点D，过点D作DE⊥AB，交直线AB于点E．设DE=x m，在Rt△BDE中，，进而求得，在Rt△ADE中，，求得，根据CD=CE-DE可得出答案．
【详解】解：设旗杆底部为点C，顶部为点D，延长CD交直线AB于点E，依题意则DE⊥AB，

则CE=30m，AB=20m，∠EAD=30°，∠EBD=60°，
设DE=x m，
在Rt△BDE中，
解得
则m，
在Rt△ADE中，，
解得m，
∴CD=CE-DE．
故答案为：12.7．
【点睛】本题考查解直角三角形的应用-仰角俯角问题，熟练掌握锐角三角函数的定义是解答本题的关键．
例3 （2022·辽宁阜新·统考中考真题）如图，小文在数学综合实践活动中，利用所学的数学知识测量居民楼的高度，在居民楼前方有一斜坡，坡长，斜坡的倾斜角为，．小文在点处测得楼顶端的仰角为，在点处测得楼顶端的仰角为（点，，，在同一平面内）．

(1)求，两点的高度差；
(2)求居民楼的高度．（结果精确到，参考数据：）
【答案】(1)9m
(2)24m

【分析】（1）过点作，交的延长线于点，在中，可得，再利用勾股定理可求出，即可得出答案．
（2）过点作于，设，在中，，解得，在中，，，，求出的值，即可得出答案．
【详解】（1）解：过点作，交的延长线于点，

在中，，，
．
．
答：，两点的高度差为．
（2）过点作于，
由题意可得，，
设，
在中，，
解得，
在中，，，
，
解得，
．
答：居民楼的高度约为．
【点睛】本题考查解直角三角形的应用仰角俯角问题、坡度坡角问题，熟练掌握锐角三角函数的定义是解答本题的关键．

在直角三角形中，除直角外，一共有5个元素，即3条边和2个锐角，由直角三角形中除直角外的已知元素，求出所有未知元素的过程，叫做解直角三角形。
1.灵活运用边角关系求边与角;
2.若所求解的直角三角形“不可直接解”,应注意设元,借助方程来解决;
3.如果图形中没有直角时,要添加垂线将其转化为直角三角形求解.


【变式1】（2023·浙江温州·校联考模拟预测）如图，一把梯子斜靠在墙上，端点A离地面的高度长为时，．当梯子底端点B沿水平方向向左移动到点，端点A沿墙竖直向上移动到点，设，则的长可以表示为（    ）

A． B． C． D．
【答案】B
【分析】利用锐角三角函数关系求出，进而表示出的长，根据即可得结果．
【详解】解：由题意可知，，
∵，
∴，故，
∵，
∴，
则：，
故选：B．
【点睛】此题主要考查了解直角三角形的应用，正确掌握相关定义是解题关键．
【变式2】（2022·河北唐山·统考三模）如图，点O为的内心，，，点M，N分别为，上的点，且．甲、乙、丙三人有如下判断：甲：；乙：四边形的面积为定值；丙：当时，的周长有最小值．则下列说法正确的是（　　）

A．只有甲正确 B．只有乙错误
C．乙、丙都正确 D．只有丙错误
【答案】D
【分析】过点O作，于点D，E，根据三角形内心可得，然后证明，可得，进而得到，然后求出可知；根据，可得四边形的面积，根据点D的位置固定，可得四边形的面积是定值；过点O作于点F，根据，，可得，，求出的周长，可得当最小，即时，的周长最小，进而可得结论．
【详解】解：如图，连接，过点O作，于点D，E，

∵点O为的内心，
∴是的平分线，
∴，
在和中，，
∴，
∴，
∴，
∵，
∴，
∴，故甲的判断正确；
∵，
∴四边形的面积四边形的面积，
∵点D的位置固定，
∴四边形的面积是定值，故乙的判断正确；
如图，过点O作于点F，

∵，，
∴，
∴，
∴的周长，
∴当最小，即当时，的周长取得最小值，
此时，不垂直于，故丙的判断错误．
故选：D．
【点睛】本题考查了三角形的内切圆与内心，角平分线的性质，等腰三角形的判定和性质，全等三角形的判定和性质，解直角三角形等知识，解决本题的关键是掌握三角形内心的定义．
【变式3】（2023·浙江温州·校联考模拟预测）甲、乙两幢完全一样的房子如图1，小聪与弟弟住在甲幢，为测量对面的乙幢屋顶斜坡M，N之间的距离，制定如下方案：两幢房子截面图如图2，，小聪在离屋檐A处3m的点G处水平放置平面镜（平面镜的大小忽略不计），弟弟在离点G水平距离3m的点H处恰好在镜子中看到乙幢屋顶N，此时测得弟弟眼睛与镜面的竖直距离．下楼后，弟弟直立站在处，测得地面点F与E，M，N在一条直线上，，，，则甲、乙两幢间距_________m，乙幢屋顶斜坡M，N之间的距离为_____________m．

【答案】     25    
【分析】过N点作交于点Q，交于点K，根据，，利用三角形函数解直角三角形即可解得．
【详解】解：如图，交于R，过N点作交于点Q，交于点K，
四边形是矩形，，

由题意得：，，
∴，即：，
∴，
∴
设，
∵，即，
∴，
∴，
∵，
∴，解得：，
∴，
故答案为：，
【点睛】本题考查解直角三角形的实际应用及分析问题、解决问题的能力．利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
【变式4】（2023·浙江金华·校考一模）金华新金婺大桥是华东第一的独塔斜拉桥，如图1是新金婺大桥的效果图．2022年4月13日开始主塔吊装作业．如图2，我们把吊装过程抽象成如下数学问题：线段为主塔，在离塔顶10米处有一个固定点米．在东西各拉一根钢索和，已知等于214米．吊装时，通过钢索牵拉，主塔由平躺桥面的位置，绕点O旋转到与桥面垂直的位置．中午休息时，此时一名工作人员在离M米的B处，在位于B点正上方的钢索上A点处挂彩旗．正好是他的身高米．
（1）主塔的高度为 _____米，（精确到整数米）
（2）吊装过程中，钢索也始终处于拉直状态，因受场地限制和安全需要，与水平桥面的最大张角在到之间即，的取值范围是 _____．（注：，）．

【答案】     82     ##
【分析】（1）过点Q作交于G点，得到，则，再由，可得，求出，再求米，即求的长；
（2）在中，，在中，米，米，，再由，由题可知，则．
【详解】解：过点Q作交于G点，

∵米，米，
∴，
∴，
∵，
∴，
∵米，
∴，
解得米，
∴米，
∵米，
∴米，
故答案为：82；
（2）解：在中，，
在中，米，米，
∴，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
故答案为：．
【点睛】本题考查解直角三角形的应用，熟练掌握直角三角形的三角函数值定义，准确计算是解题的关键．
【变式5】（2023·广西河池·校考一模）如图，一艘渔船位于小岛B的北偏东方向，距离小岛40nmile的点A处，它沿着点A的南偏东的方向航行．

(1)渔船航行多远距离小岛B最近（结果保留根号）？
(2)渔船到达距离小岛B最近点后，按原航向继续航行nmile到点C处时突然发生事故，渔船马上向小岛B上的救援队求救，问救援队从B处出发到达事故地点的最短航程是多少nmile（结果保留根号）？
【答案】(1)nmile
(2)nmile

【分析】（1）过B作于M，求出的长，即为所求；
（2）在中，勾股定理求出的长即可．
【详解】（1）解：过B作于M，

由题意，可知：，则，
在中，，nmile，
∴是等腰直角三角形，
∴，
答：渔船航行nmile距离小岛B最近；
（2）解：在中，，
∴，
答：救援队从B处出发到达事故地点的最短航程是nmile．

【点睛】本题考查解直角三角形的应用．解题的关键是添加辅助线，构造直角三角形．
核心考点五 三角函数的综合

例1 （2021·黑龙江·统考中考真题）如图，在正方形中，对角线与相交于点，点在的延长线上，连接，点是的中点，连接交于点，连接，若，．则下列结论：①；②；③；④；⑤点D到CF的距离为．其中正确的结论是（    ）

A．①②③④ B．①③④⑤ C．①②③⑤ D．①②④⑤
【答案】C
【分析】由题意易得，①由三角形中位线可进行判断；②由△DOC是等腰直角三角形可进行判断；③根据三角函数可进行求解；④根据题意可直接进行求解；⑤过点D作DH⊥CF，交CF的延长线于点H，然后根据三角函数可进行求解．
【详解】解：∵四边形是正方形，
∴，，
∵点是的中点，
∴，
∵，，
∴，则，
∵OF∥BE，
∴△DGF∽△DCE，
∴，
∴，故①正确；
∴点G是CD的中点，
∴OG⊥CD，
∵∠ODC=45°，
∴△DOC是等腰直角三角形，
∴，故②正确；
∵CE=4，CD=8，∠DCE=90°，
∴，故③正确；
∵，
∴，
∴，故④错误；
过点D作DH⊥CF，交CF的延长线于点H，如图所示：

∵点F是CD的中点，
∴CF=DF，
∴∠CDE=∠DCF，
∴，
设，则，
在Rt△DHC中，，
解得：，
∴，故⑤正确；
∴正确的结论是①②③⑤；
故选C．
【点睛】本题主要考查正方形的性质、相似三角形的性质与判定及三角函数，熟练掌握正方形的性质、相似三角形的性质与判定及三角函数是解题的关键．
例2 ．（2021·四川眉山·统考中考真题）如图，在菱形中，，对角线、相交于点，点在线段上，且，点为线段上的一个动点，则的最小值是______．

【答案】
【分析】过M点作MH垂直BC于H点，与OB的交点为P点，此时的长度最小为MH，再算出MC的长度， 在直角三角形MPC中利用三角函数即可解得MH
【详解】过M点作MH垂直BC于H点，与OB的交点为P点，此时的长度最小
∵菱形中，
∴AB=BC=AC=10，△ABC为等边三角形
∴∠PBC=30°，∠ACB=60°
∴在直角△PBH中，∠PBH=30°
∴PH=
∴此时得到最小值，
∵AC=10，AM=3,
∴MC=7
又∠MPC=60°
∴MH=MCsin60°=
故答案为：

【点睛】本题主要考查了菱形的性质与三角函数，能够找到最小值时的P点是解题关键.
例3 （2022·山东济宁·统考中考真题）知识再现：如图1，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c．
∵，
∴，
∴

(1)拓展探究：如图2，在锐角ABC中，∠A，∠B，∠C的对边分别为a，b，c．请探究，，之间的关系，并写出探究过程．
(2)解决问题：如图3，为测量点A到河对岸点B的距离，选取与点A在河岸同一侧的点C，测得AC＝60m，∠A＝75°，∠C＝60°．请用拓展探究中的结论，求点A到点B的距离．
【答案】(1)，证明见解析
(2)米

【分析】拓展研究：作CD⊥AB于点D，AE⊥BC于点E，根据正弦的定义得AE = csinB，
AE= bsin∠BCA，CD= asinB，CD = bsin∠BAC，从而得出结论；
解决问题：由拓展探究知， 代入计算即可．
【详解】（1）（拓展探究）证明：作CD⊥AB于点D，AC⊥BC于点E．

在RtΔABE中，，
同理：，
．

．
．
．
．
（2）（解答问题）解：在ΔABC中，

∴
解得：
答：点A到点B的距离为m．
【点睛】本题主要考查了解直角三角形，对于锐角三角形，利用正弦的定义，得出是解题的关键．


【变式1】（2022·黑龙江哈尔滨·统考三模）如图，折叠矩形的一边，使点落在边的点处，若，，则折痕（　　　）

A． B． C．8 D．10
【答案】B
【分析】首先根据折叠及求得EF的值，进一步知道DC的长度，后根据，其正切值相同解三角形ABF得BF的长度，从而知道AD的长度，后根据勾股定理求得AE的长度．
【详解】解：由题意，∠C=90°，
∴CE=3
∵中，∠C=90°，
∴
∵是折叠而来
∴，
∵矩形ABCD
∴
∵，
∴
∴tan∠BAF=tan∠EFC=，
即，
∴
∴
∴
故选：B
【点睛】本题考查了锐角三角函数解直角三角形，勾股定理，矩形的性质，翻折的性质，根据等量变换得到并运用其锐角三角函数相等，求线段长是解决本题的关键．
【变式2】（2022·河南南阳·统考三模）如图，射线互相垂直，，点B位于射线的上方，且在线段的垂直平分线l上，连接，．将线段绕点O按逆时针方向旋转得到对应线段，若点恰好落在射线上，则点到射线的距离是（    ）

A． B． C．4 D．
【答案】A
【分析】添加辅助线，连接，，过点作交ON与点P．根据旋转的性质，得到，在和中，，根据三角函数和已知线段的长度求出点到射线的距离．
【详解】解：如图所示，连接，，过点作交ON与点P．

∵线段绕点按逆时针方向旋转得到对应线段，
∴，，
∴，
即，
∵点在线段的垂直平分线上，
∴， ，
，
∵，
∴，
∴，
∴，
故选：A
【点睛】本题主要考查旋转的性质和三角函数．对应点到旋转中心的距离相等，对应点与旋转中心所连的线段的夹角等于旋转角，旋转前、后的图形全等．
【变式3】（2022·江苏扬州·统考一模）如图，在中，，．矩形DEFG的顶点D、E、F分别在边BC、AC、AB上，若，则矩形EDFG面积的最大值=______．

【答案】##
【分析】设ED=x ，EF=y， 过F作FH⊥AC于H，用含x和y的代数式表示出矩形EDGF的面积，再配方可求出面积的最大值．
【详解】解：设ED=x，EF=y，过F作FH⊥AC于H,

在Rt△ECD中，
∵tan∠DEC=，
∴sin∠DEC=，cos∠DEC=，
∴EC=x.
∵∠FEH+∠CED=90°，
∴∠EFH=∠DEC，
∴HE=y×sin∠EFH= y×sin∠DEC= y，
∴FH=，
∵△AHF是等腰直角三角形，
∴AH=FH=，
∵AC=AH+HE+EC=，
∴=4，
∴y=，
∴S矩形EDEF=xy=
=，
∴当x=时，矩形EDGF面积有最大值，最大值为．
故答案为： ．
【点睛】本题考查二次函数的最值，等腰直角三角形，锐角三角函数的定义，属于中档题．
【变式4】（2022·江苏苏州·校考一模）【理解概念】
定义：如果三角形有两个内角的差为，那么这样的三角形叫做“准直角三角形”．
(1)已知△ABC是“准直角三角形”，且．
①若，则______；
②若，则______；
【巩固新知】
(2)如图①，在中，，点D在边上，若是“准直角三角形”，求的长；


【解决问题】
(3)如图②，在四边形中，，且是“准直角三角形”，求的面积．


【答案】(1)①15；②10或25
(2)或
(3)的面积为48或24

【分析】（1）①根据三角形内角和定理求解即可；
②根据三角形内角和定理求解即可；
（2）根据题意可分为①当时，过点D作于H，结合勾股定理求解；②，结合相似三角形的判定和性质求解即可；
（3）过点C作于F，，交的延长线于E，设，
根据和可得，即可证明，可得，进而分情况讨论求解：当时和当．
【详解】（1）①当时，则，
∴（不合题意舍去），
当，则，
∵，
∴，
∴，
综上所述：，
故答案为：15；
②当时，则，
∴，
当，则，
∵，
∴，
∴，
综上所述：或，
故答案为：10或25；
（2）当时，如图①，过点D作于H，

在中，，
∴，
∵，
∴，
又∵，
∴，
∵，
∴，
∴，
当时，
∵，，
∴，
又∵，
∴，
∴，
∴，
∴，
综上所述：或；
（3）如图②，过点C作于F，，交的延长线于E，

设，
∵，
∴，
又∵，
∴，
又∵，
在和中，
，
∴，
∴，
当时，
又∵，
∴，
由（2）可知： ，
设，则，
∴，
∴，
∴，
当，
又∵，
∴，
又∵，
∴，
∴ ，
∴，
∴，
综上所述：的面积为48或24．
【点睛】本题考查了全等三角形的判定和性质、相似三角形的判定和性质、勾股定理和三角形内角和定理，灵活运用所学知识求解是解决本题的关键．

【新题速递】
1．（2023·上海松江·统考一模）已知中，，，，那么下列结论正确的是（    ）
A． B． C． D．
【答案】B
【分析】根据勾股定理求得斜边长，进而根据三角函数的定义即可求解．
【详解】解：如图

∵中，，，，
∴,
∴，，，，
故选：B．
【点睛】本题考查了三角函数的定义，掌握三角函数的定义是解题的关键．
2．（2022秋·安徽安庆·九年级统考期中）已知 为锐角，则的值（    ）
A． ​ B． ​ C． ​ D． ​
【答案】A
【分析】根据锐角三角函数的概念，可以用直角三角形的边进行表示，再进一步根据三角形的三边关系进行分析．
【详解】解：设在直角三角形​中，，，
故，，
则，
故选A．
【点睛】此题综合考查了锐角三角函数的概念，以及三角形的三边关系．
3．（2023春·九年级课时练习）我们都知道蜂巢是很多个正六边形组合来的．正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固．如图，某蜂巢的房孔是边长为6的正六边形，若的内接正六边形为正六边形，则的长为（    ）

A．12 B． C． D．
【答案】C
【分析】根据题意可得，则，再根据平分弧的直径垂直平分这条弧所对的弦可得，，再根据可得是等边三角形，则，最后结合三角函数即可求解．
【详解】解：连接，交于点M，连接，

∵六边形是的内接正六边形，
∴，，
∴，
∵经过圆心O，
∴，，
∴，
∵，
∴是等边三角形，
∴，
∵在中，，，，
∴，
∴，
故选C．
【点睛】本题考查了等边三角形的判定和性质、三角函数综合和圆周角定理，灵活运用所学知识求解是解决本题的关键．
4．（2023秋·河北邯郸·九年级校考期末）兴义市进行城区规划，工程师需测某楼的高度，工程师在D得用高的测角仪，测得楼顶端A的仰角为，然后向楼前进到达E，又测得楼顶端A的仰角为，楼的高为（    ）

A． B． C． D．
【答案】A
【分析】利用的正切值可表示出长，进而利用的正切函数求长，加上即为这幢教学楼的高度．
【详解】解：在中，，，
，
在中，，，
．
又，
即，
，
．
故选：A．
【点睛】本题考查了解直角三角形的应用仰角俯角问题，构造仰角所在的直角三角形，利用两个直角三角形的公共边求解是常用的解直角三角形的方法．
5．（2022秋·山东济宁·九年级统考期末）如图，由边长为1的小正方形构成的网格中，点A，B，都在格点上，以为直径的圆经过点，，则的值为(   )

A． B． C． D．
【答案】B
【分析】由格点构造直角三角形，由直角三角形的边角关系以及圆周角定理可得答案．
【详解】解：∵为直径，
∴，
∵，，
，
∵，
∴，
.
故选：B．
【点睛】本题考查圆周角定理，直角三角形的边角关系，掌握圆周角定理以及直角三角形的边角关系是正确解答的前提．
6．（2023秋·湖南邵阳·九年级统考期末）如图，在中，是的角平分线，如果，那么的值是（    ）

A． B． C． D．2
【答案】A
【分析】根据等腰三角形的性质，可得，再根据角平分线的性质及三角的面积公式得，进而即可求解．
【详解】解：，平分，
∴，
∴，
过点O作，如图，

∵平分，
∴，，
∵
∴，即：，
解得：，
∴，
故选A．
【点睛】本题主要考查等腰三角形的性质，角平分线的性质，锐角三角函数的定义，推出是解题的关键．
7．（2023秋·福建泉州·九年级统考期末）如图，在等边中，，垂足为，以，为邻边作矩形，连接交边于点，则的值为（    ）

A． B． C． D．
【答案】A
【分析】设等边的边长为a，则．根据等边三角形的性质可得，从而可由勾股定理求出．根据矩形的性质又可得出，，，即又可利用勾股定理求出．过点C作于点G，由，可得出，进而由勾股定理可求出，最后由余弦的定义即可求解．
【详解】解：设等边的边长为a，则．
∵，
∴，，
∴．
∵四边形是矩形，
∴，，，
∴．
如图，过点C作于点G，

∵，
∴，
∴，
∴，
∴．
故选A．
【点睛】本题考查等边三角形的性质，勾股定理，矩形的性质，求角的余弦值．正确作出辅助线是解题关键．
8．（2023秋·湖北鄂州·九年级统考期末）正三角形的边长为，是边上一动点，两点关于直线对称，连接并延长交直线于，连接，在点运动过程中，的最大值是（　　）

A． B． C． D．
【答案】C
【分析】如图所示（见详解），先证明四点共圆，将绕点顺时针旋转，可知，，，是等边三角形，则的最大值转换为的最大值，作的外接圆，过点作于点，的最大值为，由此即可求解．
【详解】解：∵ 两点关于直线对称，
∴，
∵
∴四点共圆，
∴，
如图所示，在上截取，

∵是等边三角形，即，
∴绕点顺时针旋转后，点与点重合，
∴，，，
∴是等边三角形，即，
∴
∴共线，    
∴，的最大值，即的最大值，
如图所示，作的外接圆，过点作于点，

∵，
∴的最大值为，
∵
∴
∴的最大值是，
故选：．
【点睛】本题主要考查动点与等边三角形的问题，三角形外接圆的性质，掌握等边三角形的性质，旋转的性质，构造等边三角形，直角三角形，运用勾股定理是解题的关键．
9．（2023·全国·九年级专题练习）如图，直线与相切于点，且，则________．

【答案】##
【分析】连接，并延长交于点，根据切线的性质，得出，再根据平行线的性质，得出，再根据垂径定理，得出，进而得出，再根据等量代换，得出，再根据余弦的定义，即可得出答案．
【详解】解：如图，连接，并延长交于点，

∵直线与相切于点，
∴，
∵，
∴，
∴，
∴，
∵，
∴，
∴．
故答案为：
【点睛】本题考查了切线的性质、平行线的性质、垂径定理、锐角三角函数，解本题的关键在熟练掌握相关的性质定理，并正确作出辅助线．
10．（2023秋·吉林长春·九年级统考期末）如图，的顶点是正方形网格的格点，则的值为__________．

【答案】
【分析】利用勾股定理和勾股定理的逆定理证明是直角三角形，再根据正切的定义进行求解即可．
【详解】解：由题意得，，
∴，
∴是直角三角形，即，
∴，
故答案为：．
【点睛】本题主要考查了求角的正切值，勾股定理和勾股定理的逆定理，证明是直角三角形是解题的关键．
11．（2023秋·江苏·九年级统考期末）如图，中，，，点为的中点，连接，的值为______．

【答案】
【分析】过点作，根据题意得出，设，则，进而得出，根据正切的定义即可求解．
【详解】解：如图所示，过点作，

∵中，，，
∴，
设，则
∵点为的中点，
∴
∵，
∴，
∴
在中，，
∴．
故答案为：．
【点睛】本题考查了求正切，正确的作出辅助线是解题的关键．
12．（2022秋·河南郑州·九年级统考期末）如图，折叠矩形的一边，使点落在边的点处，若，，则折痕______．

【答案】
【分析】由矩形的性质得，由折叠的性质得，，证得，再由，解得的值，设，则，利用矩形的性质求得，在中，由勾股定理计算求解即可．
【详解】解：∵四边形为矩形，
∴，
由折叠的性质得：，，
∵，
∴，
∴，即，
∵，
∴，
设，则，
在中，由勾股定理得，
∴，
∴，
解得，
∴，
∴，
在中，由勾股定理得，
故答案为：．
【点睛】本题考查了矩形的性质，折叠的性质，勾股定理，正切函数．解题的关键在于找出线段的数量关系，多次运用勾股定理求解．
13．（2023秋·贵州铜仁·九年级统考期末）如图所示，某施工方计划把一座山的，两点用隧道打通，并利用北斗卫星定位技术确定，，三点在东西方向的同一条直线上．在隧道没有打通之前，技术监督员李工每天需要驾车先从隧道口点向正西行驶到达点，然后再沿南偏东方向行驶到达点，接着再沿北偏东方向行驶一段路程才能到达隧道口，则隧道的长度为______．

【答案】
【分析】过点作，交于点，解，求出，解，求出，利用求出，再用，即可得解．
【详解】解：如图，过点作，交于点，则，

由题意，得：，，
在，
在，，
∴，
∴；
故答案为：．
【点睛】本题考查解直角三角形的应用．解题的关键是添加辅助线，构造直角三角形．
14．（2023秋·河南平顶山·九年级统考期末）如图，在菱形中，，，点E为边的中点，点F为边上一动点，连接，把沿所在直线折叠，得到，连接，，当为直角三角形时，线段的长为______．

【答案】或4
【分析】根据已知条件说明，所以当为直角三角形时，有和两种情况：当时，点在上，当时，取中点，连接，分两种情形分别计算即可．
【详解】解：∵点E是菱形边的中点，
，
，
，
，
当为直角三角形时，有和两种情况：
①当时，连接，过点F作于点G，如图：

在菱形中，，
和都是等边三角形，
，
，，
，可知点在上，
由翻折可知：，
，
，
，
，
，
，
解得
∴；
②当时，取中点H，连接，如图，

∴
，，
，
∴在同一条直线上，
∴四边形是平行四边形，
，
，
是等边三角形，
．
综上所述：线段的长为或．
故答案为：或．
【点睛】本题考查了翻折变换，菱形的性质，等边三角形的判定与性质，勾股定理，解决本题的关键是掌握翻折的性质．

15．（2023春·湖北省直辖县级单位·九年级校联考阶段练习）计算：．
【答案】1
【分析】根据有理数的混合运算顺序，先算、、、，再进行加减计算即可．
【详解】解：原式


【点睛】本题考查了有理数的混合运算、特殊角的三角函数值、绝对值的性质、二次根式及任何非零数的零次幂等于1，能综合运用这些知识是计算本题的关键．
16．（2023春·河南郑州·九年级河南省实验中学校考阶段练习）某校安装了红外线体温检测仪（如图1），该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温，其红外线探测点O可以在垂直于地面的支杆上下调节（如图2），探测最大角（）为，探测最小角（）为，已知该设备在支杆上下调节时，探测最大角及最小角始终保持不变．若要求测温区域的宽度为2.53米，请你帮助学校确定该设备的安装高度．（结果精确到0.01米，参考数据：，，，，，）

【答案】1.84米
【分析】首先根据题意表示出，然后利用三角函数表示出和，然后列方程求解即可．
【详解】解：根据题意可知，（米）．
在中，，
∴．
在中，
，
∴，
∴（米），
∴（米）．
答：该设备的安装高度约为1.84米．
【点睛】本题主要考查了解直角三角形的应用，熟练掌握锐角三角函数定义是解决本题的关键．
17．（2023秋·湖北随州·九年级统考期末）如图，内接于⊙，是⊙的直径，切⊙于点B，E为上一点，且，延长交于点D．

(1)求证：；
(2)若⊙的半径为5，，求的长．
【答案】(1)见解析
(2)6

【分析】（1）由直径所对的圆周角是直角和切线的性质得到，则，再由等边对等角，对顶角相等证明，推出，即可证明；
（2）由得到，设，则，，由勾股定理建立方程，解方程即可得到答案．
【详解】（1）证明：∵是的直径，切于点B，
∴，
∴，
∵，
∴，
∴，
∴；
（2）解：∵，，
∴，
设，则，，
在中，由勾股定理得，
∴，
解得，（舍去），
∴．

【点睛】本题主要考查了切线的性质，等腰三角形的性质与判定，直径所对的圆周角是直角，勾股定理，锐角三角函数等等，灵活运用所学知识是解题的关键．
18．（2023·江苏宿迁·统考一模）如图，梯形是某水坝的横截面示意图，其中，坝顶，坝高，迎水坡的坡度为．

(1)求坝底的长；
(2)为了提高堤坝防洪抗洪能力，防汛指挥部决定在背水坡加固该堤坝，要求坝顶加宽，背水坡坡角改为．求加固总长5千米的堤坝共需多少土方？（参考数据：；结果精确到）
【答案】(1)
(2)加固总长5千米的堤坝共需土方

【分析】（1）过点作于，可得：，利用坡比求出的长，易得为等腰直角三角形，进而求出的长，利用，即可得解；
（2）过点F作于G，求出梯形的面积，再乘以总长即可得出结果．
【详解】（1）解：过点作于，

则四边形是矩形，
∴，
∵，
∴，
∴，
∵，
∴四边形是等腰梯形
∴
∴是等腰直角三角形
∴，
∴；
（2）解：过点F作于G，则四边形是矩形，

∴，
∵，
∴，
∴，
∴，
∴加固总长5千米的堤坝共需土方：．
【点睛】本题考查解直角三角形的实际应用．解题的关键是添加辅助线，构造直角三角形．
19．（2023春·河南驻马店·九年级驻马店市第二初级中学校考开学考试）某校“趣味数学”社团开展了测量本校旗杆高度的实践活动．“综合与实践”小组制订了测量方案，并完成了实地测量．他们在该旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离．为了减小测量误差，该小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如表（不完整）
课题
测量旗杆的高度
成员
组长：xxx组员：xxx，xxx，xxx
测量工具
角度的仪器，皮尺等
测量示意图

说明：线段GH表示学校旗杆，测量角度的仪器的高度，测点A，B与H在同一条水平直线上，A，B之间的距离可以直接测得，且点G，H，A，B，C，D都在同一竖直平面内，点C，D，E在同一条直线上，点E在上．
测量数据
测量项目
第一次
第二次
平均值
的度数



的度数



A，B之间的距离



…
…


(1)任务一：两次测量A，B之间的距离的平均值　 　m
(2)任务二：根据以上测量结果，请你帮助该“综合与实践”小组求出学校旗杆GH的高度．（参考数据：，，，，，）
(3)任务三：该“综合与实践”小组在制定方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳．你认为其原因可能是什么？（写出一条即可）
【答案】(1)6
(2)旗杆GH的高度为米
(3)没有太阳光，或旗杆底部不可能达到相等（答案不唯一）

【分析】（1）根据两次测量结果直接求平均值就可以得到答案；
（2）设，解直角三角形即可得到结论；
（3）根据题意得到没有太阳光，或旗杆底部不可能达到相等（答案不唯一）．
【详解】（1）解：，
故答案为：6；
（2）设，
在中，，，
∵，
∴，
在中，，，
∵，，
∵，
∴，
∴，
∴，
答：旗杆GH的高度为米；
（3）没有太阳光，或旗杆底部不可能达到相等．

【点睛】本题考查的是解直角三角形的应用﹣仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．
20．（2022秋·河北石家庄·九年级校联考期末）如图（1），菱形中，，点O在边上（不可与点B重合，可与点C重合），以O为圆心，长为半径的圆O与直线交于点E，与直线交于点F，设．

(1)如图（2），当点E与点C重合时，连接．
①__________；
②求的长度．
(2)当点E在线段上时，如图（3），连接，求阴影部分的面积S与x之间的关系式．（不要求写出x的取值范围）
(3)直接写出圆O与线段只有一个交点时x的取值范围__________．
【答案】(1)②5；①；
(2)；
(3)或

【分析】（1）①直接利用半径等于直接的一半即可求解；
②推出，，由，，则，利用勾股定理即可求解；
（2）由，，推出，根据阴影面积等于半圆面积减去，列式计算即可求解；
（3）分当与相切于点G时，当过点A时，当过点D时，三种情况讨论，画出图形，即可求解．
【详解】（1）解：①当点E与点C重合时，，
∵菱形中，，
∴，
故答案为：5；
②∵是的直径，
∴，
又，
∴，
∴，
设，则，
∵，即，
解得（负值已舍），
∴；
（2）解：∵是的直径，
∴，
又，，
∴，
∴
∴；
（3）解：当与相切于点G时，与线段只有一个交点，连接，
过A作于点Ｉ，则四边形为矩形，

由题意得，，
同理求得，
此时，；
当过点A时，连接，过O作于点H，

∵，，
又∵，，
∴，
∴，
∴，
即当时，过点A，此时与线段有两个交点；
当过点D时，，

此时，点O在点C处，
∴，
综上，与线段只有一个交点时，或．
故答案为：或．
【点睛】本题考查了切线的性质，勾股定理，正切函数，菱形的性质，灵活运用这些性质解决问题是解题的关键．