

2024高考数学一轮总复习(导与练)第二章 第7节 函数的图象
展开第7节 函数的图象
[选题明细表]
知识点、方法 | 题号 |
函数图象的识别 | 2,4,5,10 |
函数图象的理解、变换 | 1,3,6,11 |
函数图象的应用 | 7,8,9,12,13,14,15 |
1.若函数f(x)=的图象如图所示,则f(-3)等于( C )
A.- B.-
C.-1 D.-2
解析:由图象可得a·(-1)+b=3,ln(-1+a)=0,解得a=2,b=5,所以f(x)=故f(-3)=2×(-3)+5=-1.
2.已知lg a+lg b=0(a>0,且a≠1,b>0,且b≠1),则函数f(x)=ax与g(x)=lox的图象可能是( B )
解析:由lg a+lg b=0可知lg ab=0,ab=1,
解得 a=,故函数f(x)=ax与函数g(x)=lox的单调性相同.
3.要得到函数y=log2(2x+4)的图象,只需将函数 y=log2(x+2)的图象( C )
A.向左平移2个单位长度
B.向右平移2个单位长度
C.向上平移1个单位长度
D.向下平移1个单位长度
解析:y=log2(2x+4)=log2[2(x+2)]=log22+log2(x+2)=1+log2(x+2),故只需将函数y=log2(x+2)的图象向上平移1个单位长度即可.
4.(2023·江苏淮安模拟)已知函数f(x)=,则f(x)的大致图象是( D )
解析:函数f(x)=的定义域为{x|x≠±1},
f(-x)==f(x),则f(x)为偶函数,其图象关于y轴对称,可排除选项A;
由f(x)=0,可得x=0,可排除选项C;
当0<x<1时,|x|-1<0,ex-e-x>0,
则f(x)<0,可排除选项B.
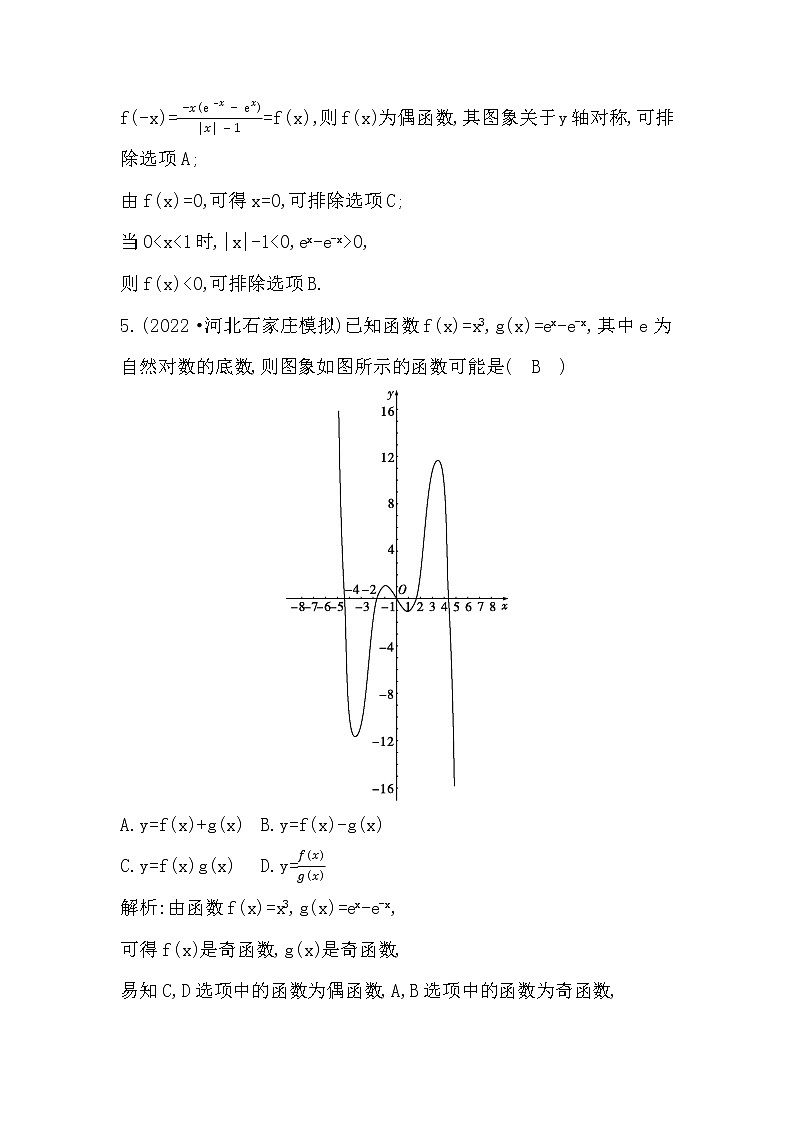
5.(2022·河北石家庄模拟)已知函数f(x)=x3,g(x)=ex-e-x,其中e为自然对数的底数,则图象如图所示的函数可能是( B )
A.y=f(x)+g(x) B.y=f(x)-g(x)
C.y=f(x)g(x) D.y=
解析:由函数f(x)=x3,g(x)=ex-e-x,
可得f(x)是奇函数,g(x)是奇函数,
易知C,D选项中的函数为偶函数,A,B选项中的函数为奇函数,
因为函数图象关于原点对称,所以函数为奇函数,排除C,D选项,
又当x→+∞时,y→-∞,排除A选项.
6.如图所示是一个无水游泳池,ABCDA′B′C′D′是一个四棱柱,游泳池是由一个长方体切掉一个三棱柱得到的.现在向泳池注水,如果进水速度是均匀的(单位时间内注入的水量不变),水面与AB的交点为M,则AM的高度h随时间t变化的图象可能是( A )
解析:由题意可知,当往游泳池内注水时,游泳池内的水呈“直棱柱”状,且直棱柱的高不变,刚开始水面面积逐渐增大,水的高度增长得越来越慢,当水面经过点D后,水面的面积为定值,水的高度匀速增长,故符合条件的函数图象为A选项中的图象.
7.函数f(x)=x2-2|x|-m的零点有两个,则实数m的取值范围为( B )
A.-1<m<0 B.m>0或m=-1
C.m>0或-1≤m<0 D.0<m<1
解析:在同一平面直角坐标系内作出函数y=x2-2|x|和直线y=m的图象,由函数f(x)=x2-2|x|-m的零点可知,当m>0或m=-1时,两函数的图象有2个交点.
8.已知函数y=f(x)是定义在区间[-3,3]上的偶函数,它在区间[0,3]上的图象是如图所示的一条线段,则不等式f(x)+f(-x)>x的解集为 .
解析:由题意,函数f(x)过点(0,2),(3,0),则y=f(x)=-x+2,x∈[0,3].
又因为f(x)是偶函数,图象关于y轴对称,
所以f(x)=f(-x),所以2f(x)>x.
作出函数f(x)在[-3,3]上的图象,如图.
当x∈[-3,0)时,y=2f(x)的图象恒在y=x的上方,
当x∈[0,3]时,令2f(x)=x,得x=,即当x∈[0,)时,满足2f(x)>x.
故f(x)+f(-x)>x的解集为{x|-3≤x<}.
答案:{x|-3≤x<}
9.已知函数f(x)=若x1,x2,x3均不相等,且f(x1)=f(x2)=f(x3),则x1·x2·x3的取值范围是 .
解析:不妨设x1<x2<x3,由图可得,|log2x1|=|log2x2|=-x3+3∈(0,1),
所以log2x1=-log2x2,即x1x2=1,
由f(x1)=f(x2)=f(x3)得,x3∈(2,3),
所以x1·x2·x3的取值范围是(2,3).
答案:(2,3)
10.(多选题)函数f(x)=的大致图象可能为( AD )
解析:因为x→0时,f(x)→0,所以排除B,C,
又x>0时,指数函数y=ex是爆炸增长型函数,y=xln x增加速度一般,
所以x→+∞时,→0,所以A,D都满足,所以A,D正确.
11.已知定义在区间(0,2)上的函数y=f(x)的图象如图所示,则y=-f(2-x)的图象为( B )
解析:法一 由定义在(0,2)上的函数y=f(x)的图象可知f(x)=
当0<2-x<1,即1<x<2时,f(2-x)=2-x,
当1≤2-x<2,即0<x≤1时,f(2-x)=1,
所以y=-f(2-x)=根据一次函数的性质,结合选项可知,选项B正确.
法二 y=f(x)y=f(-x)y=f(2-x)
y=-f(2-x).
12.已知f(x)=若|f(x)|≥ax在x∈[-1,1]上恒成立,则实数a的取值范围是( C )
A.(-∞,-1]∪[0,+∞)
B.[0,1]
C.[-1,0]
D.(-1,0)
解析:作出y=|f(x)|,y=ax在[-1,1]上的图象如图所示,因为
|f(x)|≥ax在x∈[-1,1]上恒成立,所以y=|f(x)|的图象在y=ax的图象的上方(可以部分点重合),且|f(-1)|=|1-2|=1,
令3x-2=0,得x=,
所以A(-1,1),B(,0),根据图象可知,
当y=ax经过点A(-1,1)时,a有最小值,amin=-1,当y=ax经过点B(,0)时,a有最大值,amax=0.综上可知,a的取值范围是[-1,0].
13.直线y=k(x-1)+1与曲线y=有两个不同的交点(x1,y1),(x2,y2),则x1+x2+y1+y2= .
解析:由于不论k取何值,直线y=k(x-1)+1均过定点(1,1),分析曲线y=可知,函数y=的图象关于点(1,1)对称,因此两个交点关于点(1,1)对称,因此x1+x2=2,y1+y2=2,所以x1+x2+y1+y2=4.
答案:4
14.若x·log2x=3,y·2y=3,z·ln z=3,则x,y,z由小到大的顺序是 .
解析:依题意,x>0,y>0,z>0,x·log2x=3⇔log2x=,y·2y=3⇔2y=
,z·ln z=3⇔ln z=.因此,x·log2x=3成立的x值是函数y1=log2x与y4=的图象交点的横坐标t1,y·2y=3成立的y值是函数y2=2x与y4=的图象交点的横坐标t2,z·ln z=3成立的z值是函数y3=ln x与y4=的图象交点的横坐标t3,在同一平面直角坐标系内作出函数y1=log2x,y2=2x,y3=ln x,y4=的图象,如图,
观察图象得t2<t1<t3,即y<x<z,所以x,y,z由小到大的顺序是y<x<z.
答案:y<x<z
15.已知[x]表示不超过x的最大整数,定义函数f(x)=x-[x].有下列结论:
①函数的图象是一条直线;②函数f(x)的值域为[0,1);③方程f(x)=有无数个解;④函数在R上单调递增.
其中错误的是 (填写所有错误结论的序号).
解析:由题意知,对任意的实数x,若存在整数k,满足k≤x<k+1,
则[x]=k,
所以f(x)=x-[x]=
作出部分图象,如图所示,
由图可知,函数的图象在每个单位区间内是一条线段,不是一条直线,故①错误;
由图可知,y∈[0,1),故函数f(x)的值域为[0,1),故②正确;
由图可知,直线f(x)=与函数的图象有无数个交点,即f(x)=有无数个解,故③正确;
由图可知,函数在每个单位区间内单调递增,但在整个定义域R内不具备单调性,故④错误.
答案:①④
2024高考数学一轮总复习(导与练)第二章第1节 函数的概念及其表示: 这是一份2024高考数学一轮总复习(导与练)第二章第1节 函数的概念及其表示,共9页。
2024高考数学一轮总复习(导与练)第二章 培优课(一) 抽象函数的性质: 这是一份2024高考数学一轮总复习(导与练)第二章 培优课(一) 抽象函数的性质,共4页。试卷主要包含了已知定义在R上的函数f满足等内容,欢迎下载使用。
2024高考数学一轮总复习(导与练)第二章 第9节 函数模型及其应用: 这是一份2024高考数学一轮总复习(导与练)第二章 第9节 函数模型及其应用,共12页。












