江苏省南京市江北新区2022-2023学年下学期期中学情分析样题八年级数学试题

这是一份江苏省南京市江北新区2022-2023学年下学期期中学情分析样题八年级数学试题，共10页。试卷主要包含了本试卷共6页等内容，欢迎下载使用。

Vb r 2022－2023学年度第二学期期中学情分析样题
八年级数学
注意事项：
1．本试卷共6页．全卷满分100分．考试时间为100分钟．考生答题全部答在答题卡上，答在本试卷上无效．
2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上．
3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案．答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效．
4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．
一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的序号填涂在答题卡上）
1．下列图形中，既是轴对称图形，又是中心对称图形的是


A．
B．
C．
D．

2．以下调查中，适合普查的是
A．了解班级每位学生穿鞋的尺码
C．了解长江水质情况
B．了解中学生的心理健康状况
D．了解市民坐高铁出行的意愿
3．“向上抛掷一枚质地均匀的骰子，正面向上的点数是偶数”这一事件是
A．必然事件
B．随机事件
C．不可能事件
D． 确定事件
4．下列命题正确的是
A．矩形的对角线互相垂直
C．对角线互相平分的四边形是平行四边形
B．菱形的对角线相等
D．四个角都相等的四边形是正方形
5．如图，在四边形ABCD中，E、F、G、H分别是线段AD、BD、BC、AC的中点，要使
四边形EFGH是菱形，需添加的条件是
B

C
A
F
E
H
G
D
A．AC = BD
B．AC⊥BD
y
C．AB = CD
D．AB⊥CD
（第6题）
D
C
B
A
x
O




（第5题）

6．在平面直角坐标系中，□ABCD的顶点坐标分别是A（0，1）、B（a，b）、C（3，－2）
则D的坐标是
A．（－a＋3，－b＋1）
C．（－a－3，－b＋1）
B．（－a－3，－b－1）
D．（－a＋3，－b－1）
二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
7．为了解某市八年级学生的身高情况，从中抽测了1 500名学生进行调查，在这次调查中，
样本容量是　 ▲ ．
8．一个不透明袋中装有5个红球、3个黑球、2个白球，每个球除颜色外完全相同，从袋中
任意摸出一个球，那么摸出　 ▲　 球的可能性最大（选填“红”、“黑”或“白”）．
9．一次数学测试后，某班40名学生的成绩被分成4组，第1～3组的频数分别为12，10，
6，则第4组的频率是　 ▲　 ．
10．在□ABCD中，若∠B+∠D=100°，则∠A＝　 ▲ 　°．
11．如图，□ABCD的对角线AC、BD相交于点O，若AB=3，AC+BD=12，则△AOB的周长为 ▲ ．
12．空气的主要成分是：氮气约占78%，氧气约占21%，其他微量气体约占1%．为描述上
述信息，最合适的统计图是　 ▲　 ．
13．如图，菱形ABCD的对角线AC 、BD相交于点O，OE⊥AD于点E，AC=8，BD=6，则OE的长为 ▲ ．
14．如图，在矩形ABCD中，AB＝3，点E在AD上，DE＝1．若EC平分∠BED，则BC
（第14题）

E
D
C
B
A
（第13题）
O
E
D
C
B
A
的长为 ▲ ．
（第11题）
A
B
C
D
O





15. 如图，在正方形ABCD中，AB = 2，E、F分别为AD、CD的中点，连接AF、BE，M、N分别为BE、AF的中点，连接MN．则MN的长为 ▲ ．
（第15题）
A
E
B
C
D
F
N
M
（第16题）
D
C
B
A
16．如图，在四边形ABCD中，AB=BC=CA，∠ADC=30°，若AD=4，CD=3，则对角线BD的长为 ▲ ．







三、解答题（本大题共10小题，共68分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
（第17题）
F
E
D
C
B
A
17．（5分）如图，在□ABCD中，点E、F分别在AD和BC上，且AE＝CF．
求证：四边形BEDF是平行四边形．




社团喜爱情况扇形统计图
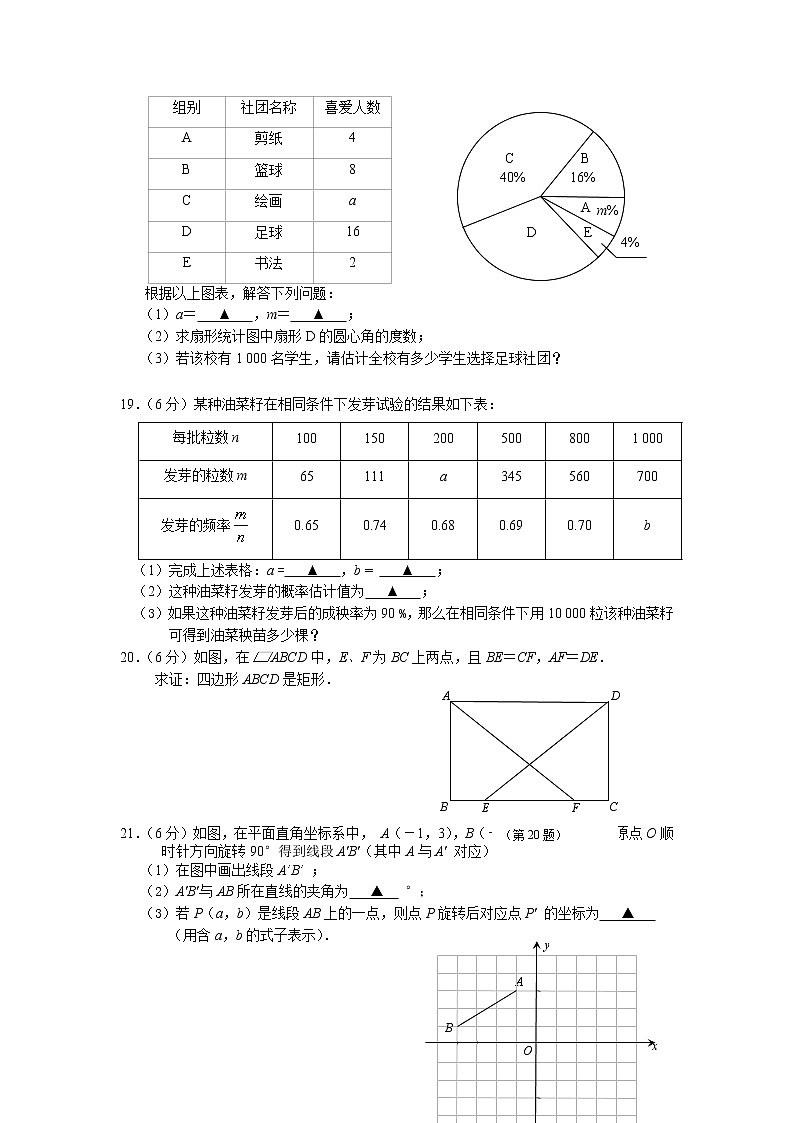
18．（6分）为了落实“双减”政策，某校开展课后延时服务，准备开设剪纸、篮球、绘画、足球、书法五种社团．为了解同学们的喜爱情况，学校随机调查了本校部分同学，然后利用所得数据绘制成如图不完整的统计图表．
社团喜爱情况频数分布表
组别
社团名称
C
B
A
D
40%
16%
4%
m%
E
喜爱人数
A
剪纸
4
B
篮球
8
C
绘画
a
D
足球
16
E
书法
2
根据以上图表，解答下列问题：
（1）a＝ ▲ ，m＝ ▲ ；
（2）求扇形统计图中扇形D的圆心角的度数；
（3）若该校有1 000名学生，请估计全校有多少学生选择足球社团？

19．（6分）某种油菜籽在相同条件下发芽试验的结果如下表：
每批粒数n
100
150
200
500
800
1 000
发芽的粒数m
65
111
a
345
560
700
发芽的频率
0.65
0.74
0.68
0.69
0.70
b
（1）完成上述表格：a = ▲ ，b = ▲ ；
（2）这种油菜籽发芽的概率估计值为 ▲ ；
（3）如果这种油菜籽发芽后的成秧率为90 %，那么在相同条件下用10 000粒该种油菜籽可得到油菜秧苗多少棵？
20．（6分）如图，在□ABCD中，E、F为BC上两点，且BE＝CF，AF＝DE．
（第20题）

C
E
D
B
A
F
求证：四边形ABCD是矩形．






21． （6分）如图，在平面直角坐标系中， A（－1，3），B（－4，1），线段AB绕原点O顺时针方向旋转90°得到线段A′B′（其中A与A′ 对应）．
（1）在图中画出线段A’B’ ；
（2）A′B′与AB所在直线的夹角为 ▲ °；
（3）若P（a，b）是线段AB上的一点，则点P旋转后对应点P′ 的坐标为 ▲
（第21题）
A
B
O
x
y
（用含a，b的式子表示）．









22. （6分）如图，D、E、F分别是△ABC各边的中点.
（1）求证：四边形ADEF是平行四边形；
（2）若AB＝10，AC＝6，BC＝8，则四边形ADEF的面积为 ▲ ．
（第22题）

C
A
D
E
F
B
















23. （8分）如图，在□ABCD中，E、F分别为AD、BC的中点，点M、N在对角线AC上，且AM＝CN．
（1）求证：四边形EMFN是平行四边形；
（2）当△ABC满足条件 ▲ 时，□EMFN是菱形．
A
D
C
B
E
F
M

N
（第23题）








24. （8分）如图，四边形ABCD是平行四边形，E为AB上一点．
（1）如图①，只用无刻度直尺在CD上作出点F，使得四边形AECF为平行四边形；
（2）如图②，用直尺和圆规作出矩形EFGH，使得点F、G、H分别在BC、CD、DA上；
（保留作图痕迹，写出必要的文字说明）
①
D
A
E
A
B
C
E
D
②

B
C


25. （8分）如图，在正方形ABCD中，E为对角线AC上一点，连接DE，过点E作EF⊥DE交AB于点F，连接DF交AC于点G．
（1）求证：EF＝DE；
（第25题）
A
G
E
D
C
B
F
（2）若DG＝4，GF＝2，则GE＝ ▲ .







26.（9分）在菱形ABCD中，E、F分别是BC、CD上点，AE=AF.
（1）如图①，若∠B为直角.求证：CE =CF；
E
F
D
C
B
A
①









（2） 如图②，若∠B为钝角.求证：CE =CF；
C
F
E
D
B
A
②







（3）若∠B为锐角，上述结论是否成立？若成立，请证明；若不成立，请画出反例.











2022－2023学年度第二学期期中学情分析样题
八年级数学
数学试卷参考答案及评分标准
说明：本评分标准每题给出了一种或几种解法供参考．如果考生的解法与本解答不同，参照本评分标准的精神给分．
一、选择题（本大题共6小题，每小题2分，共12分）
题号
1
2
3
4
5
6
答案
C
A
B
C
C
D



二、填空题（每小题2分，共20分，
7．1500
8．红
9．0.3
10．130°
11．9
12．扇形统计图
13．
14．5
15．
16．5
三、解答题（本大题共10小题，共68分）
17．（本题5分）
证明：∵四边形ABCD是平行四边形，

F
E
D
C
B
A
∴AD∥BC， 1分
AD＝BC． 2分
∵AE＝CF
∴AD－AE＝BC－CF， 3分
即DE＝BF． 4分
∵DE∥BF，
∴四边形BEDF是平行四边形． 5分
18．（本题6分）
解：（1）20，8； 2分
（2）360°×＝115.2°； 4分
（3）1000×＝320（人）；
答：估计全校有320人选择足球社团． 6分

19．（本题6分）
解：（1）136，0.70； 2分
（2）0.70； 4分
（3）1000×0.70×90%＝6300（棵）
答：用10000粒该种油菜籽可得到油菜秧苗6300棵． 6分
20．（本题6分）
证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB＝CD． 1分
∴∠B＋∠C＝180°． 2分

C
E
D
B
A
F
∵BE＝CF，
∴BE＋EF＝CF＋EF，即BF＝CE． 3分
在△ABF和△DCE中，
∵AB＝CD，BF＝CE，AF＝DE，
∴△ABF≌△DCE． 4分
∴∠B＝∠C． 5分
∵∠B＋∠C＝180°．
∴∠B＝∠C＝90°．
∴平行四边形ABCD是矩形． 6分
y
A
B
O
x
A'
B'
21．（本题6分）
（1）





2分
（2）90 4分
（3）（b，－a） 6分


C
A
D
E
F
B
22．（本题6分）
（1）证明：∵D、E分别是AB、BC的中点，
∴DE∥AC，DE＝AC． 2分
∵F是AC的中点，
∴AF＝AC． 3分
∴DE∥AF，DE＝AF．
∴四边形ADEF是平行四边形． 4分
（2）12． 6分
23．（本题8分）
证明：（1）∵四边形ABCD是平行四边形，
∴ AD∥BC，AD＝BC． 1分
∴ ∠EAM＝∠FCN． 2分
∵ E，F分别是AD，BC的中点，
∴AE＝AD，CF＝BC，
又AD＝BC，
∴ AE＝CF． 3分
∵ AM＝CN，
∴ △AEM≌△CFN．
∴ EM＝FN，∠AME＝∠CNF． 4分
∵∠AME＋∠EMN＝180°，∠CNF＋∠FNM＝180°．
∴ ∠EMN＝∠FNM．
∴ EM∥FN． 5分
∴ 四边形EMFN是平行四边形． 6分
（2）AB⊥AC或∠BAC＝90° 8分
E
A
D


B
C
F

24.（本题8分）
（1）


D
A
E
B
C
F

O

G

H

4分
（2）


8分
25．（本题8分）
（1）证明：过点E分别作EM⊥AD于点M，EN⊥AB于点N，
C

A
G
E
D
B
F
N

M
∵四边形ABCD是正方形，
∴∠BAD＝∠ABC＝90°，AB＝BC． 1分
∴∠BAC＝∠ACB＝45°．
∴∠BAC＝∠DAC＝45°．
∴AC平分∠BAD．
∵EM⊥AD，EN⊥AB，
∴EM＝EN． 2分
∠EMA＝∠ENA＝90°． 3分
∴∠MEN＝360°－∠EMA－∠BAD－∠ENA＝90°．
∴∠MEF＋∠FEN＝90°.
∵EF⊥DE，
∴∠DEF＝90°．
∴∠MEF＋∠DEM＝90°.
∴∠DEM＝∠FEN. 4分
在△DEM和△FEN中，
∵∠DME＝∠ENF，EM＝EN，∠DEM＝∠FAN，
∴△DEM≌△FEN． 5分
∴EF＝ED． 6分
（2） 8分
26．（本题9分）
（1）证明：∵四边形ABCD是菱形，∠B为直角，
∴四边形ABCD是正方形.
∴∠D＝∠B＝90°，AB＝AD＝CD＝CB． 1分
在Rt△ADF和Rt△ABE中，∠D＝∠B＝90°，
∵AD＝AB， AF＝AE，
∴Rt△ADF≌Rt△ABE． 2分
∴DF＝BE．
∴CD－DF＝CB－BE．
即CF＝CE． 3分
（2）证明：延长CD、CB，过点A分别 作AM⊥CD于点M， AN⊥CB于点N，
4分
∵四边形ABCD是菱形，
∴∠ADC＝∠ABC，AB＝AD＝CD＝CB．
∴∠ADM＝∠ABN．
∵AM⊥CD， AN⊥CB，
∴∠AMD＝∠ANB．
在△ADM和△ABN中，
∵∠ADM＝∠ABN，∠AMD＝∠ANB ，AD＝AB，
∴△ADM≌△ABN． 5分
∴AM＝AN，DM＝BN．
C
F
E
D
A
B
N
M
在Rt△AMF和Rt△ANE中，∠AMF＝∠ANE＝90°，
∵AM＝AN，AF＝AE，
∴Rt△AMF≌Rt△ANE． 6分
∴MF＝NE．
∴MF－MD＝NE－NB．
即DF＝BE．
∵DC＝BC，
∴DC－DF＝BC－BE．
即CF＝CE． 7分
（2）不成立 8分

D
C
B
A
E
F






9分