圆综合练习1(无答案)

圆综合练习1

1.如图，已知AB是⊙O的弦，OB＝4，∠OBC＝30°，点C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD、DB．

（1）当∠ADC＝18°时，求∠DOB的度数；

（2）若AC＝2，求证△ACD∽△OCB．

2.如图，以△ABC的BC边为直径作⊙O，分别交AC、AB于E、F两点，过A作⊙O的切线，切点为D，且点E、F为劣弧的三等分点．

（1）求证：AD∥BC；

（2）求∠DAC的大小．

3.如图，在直角坐标系中，点B（－1－ ，0），C（1＋ ，0），△ABC的内切圆的圆心是I（－1，1），求△ABC的面积．

4.　AB为⊙O的直径，C为⊙O上一点，若直线CD与⊙O相切于点C，AD⊥CD，垂足为D．

（1）求证：△ADC∽△ACB；

（2）如果把直线CD向下平行移动，如图（2），直线CD交⊙O于C、G两点，若题目中的其他条件不变，且AG＝4，BG＝3，求tan∠DAC的值．

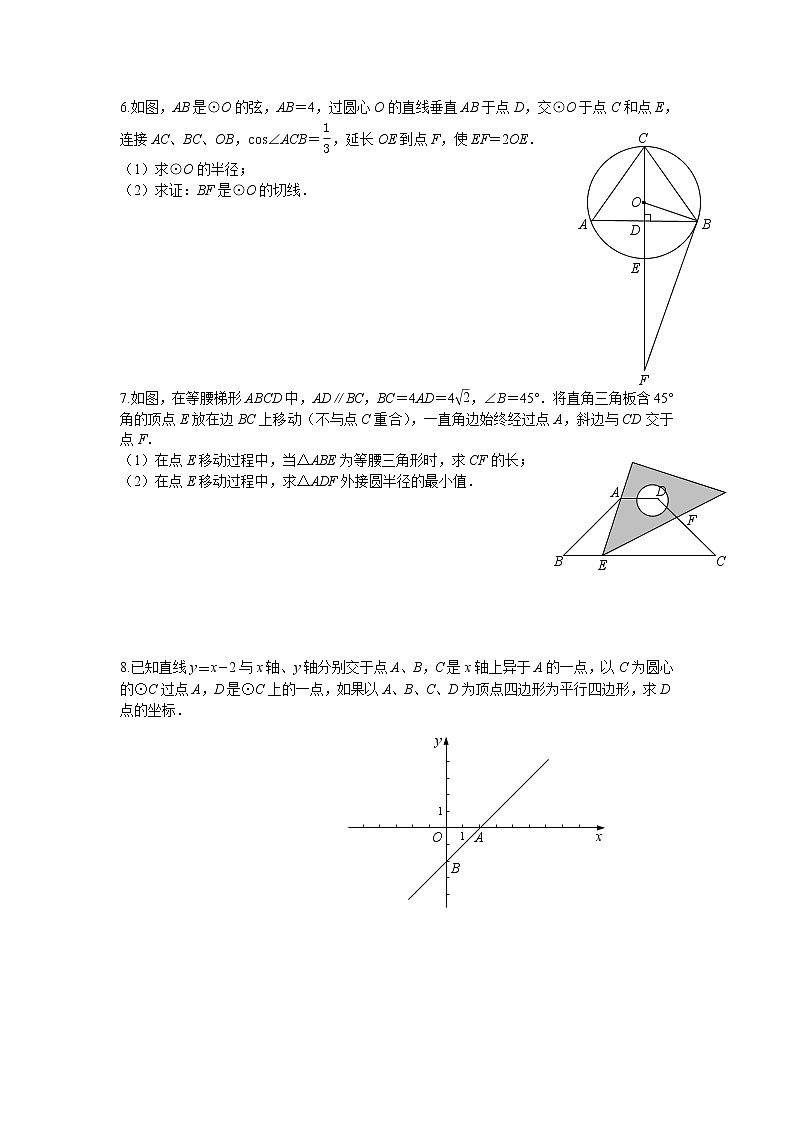
6.如图，AB是⊙O的弦，AB＝4，过圆心O的直线垂直AB于点D，交⊙O于点C和点E，连接AC、BC、OB，cos∠ACB＝  ，延长OE到点F，使EF＝2OE．

（1）求⊙O的半径；

（2）求证：BF是⊙O的切线．

7.如图，在等腰梯形ABCD中，AD∥BC，BC＝4AD＝4，∠B＝45°．将直角三角板含45°角的顶点E放在边BC上移动（不与点C重合），一直角边始终经过点A，斜边与CD交于点F．

（1）在点E移动过程中，当△ABE为等腰三角形时，求CF的长；

（2）在点E移动过程中，求△ADF外接圆半径的最小值．

8.已知直线y＝x－2与x轴、y轴分别交于点A、B，C是x轴上异于A的一点，以C为圆心的⊙C过点A，D是⊙C上的一点，如果以A、B、C、D为顶点四边形为平行四边形，求D点的坐标．

9.如图，⊙O的圆心在坐标原点，半径为2，直线y＝x＋b（b＞0）与⊙O交于A，B两点，点O关于直线y＝x＋b的对称点为点O′．

（1）求证：四边形OAO′B是菱形；

（2）当点O′ 落在⊙O上时，求b的值．

10.如图，⊙M与y轴相切于点C，与x轴交于点A（2－ ，0）、点B（2＋ ，0），D是劣弧上一点，且＝  ，P是⊙M上一个动点．如果以P、A、D、B为顶点的四边形是梯形，求∠PAD的度数为．

11.如图，P为⊙O外一点，PA、PB为⊙O的切线，A、B为切点，AC为⊙O的直径，PO交⊙O于点E．

（1）试判断∠与的数量关系，并说明理由．

（2）若⊙O的半径为4，P是⊙O外一动点，是否存在点P，使四边形PAOB为正方形？若存在，请求出PO的长，并判断点P的个数及其满足的条件；若不存在，请说明理由．

12.如图，点C在以AB为直径的半圆O上，延长BC到点D，使得CD＝BC，过点D作DE⊥AB于点E，交AC于点F，点G为DF的中点，连接CG、OF、FB．

（1）求证：CG是⊙O的切线；

（2）若△AFB的面积是△DCG的面积的2倍，求证：OF∥BC．

13.如图，在△ABC中，AB＝AC，且⊙O内切于△ABC．D、E、F是切点，CF交⊙O于G，EG延长线交BC于M，AG交⊙O于K．

（1）求证：△MCG∽△MEC；

（2）若EM⊥BC，求cos∠FAK的值．

14.已知矩形ABCD中，半径为r的两个等圆⊙O1、⊙O2外切，且⊙O1与边AB、BC相切，⊙O2与边BC相切．点E是边CD上一点，将△ADE沿AE翻折得△AD′E，AD′ 恰好与⊙O2相切于点D′．若AD＝3，折痕AE的长为 ．

（1）求r的值；

（2）求证：矩形ABCD为正方形．

15.如图，△ABC的内心为I，过点A作直线BI的垂线，垂足为H，且直线AH交BC于F．设D、E、G分别为内切圆I与边BC、CA、AB的切点，求证：

（1）AG＝DF；   （2）D、H、E三点共线．

16.如图，已知AB为⊙O的直径，过⊙O上的点C的切线交AB的延长线于点E，AD⊥EC于点D且交⊙O于点F，连接BC，CF，AC．

（1）求证：BC＝CF；

（2）若AD＝6，DE＝8，求BE的长；

（3）求证：AF＋2DF＝AB．

17.如图，已知在△ABC中，AB＝15，AC＝20，cotA＝2，P是边AB上的一个动点，⊙P的半径为定长．当点P与点B重合时，⊙P恰好与边AC相切；当点P与点B不重合，且⊙P与边AC相交于点M和点N时，设AP＝x，MN＝y．

（1）求⊙P的半径；

（2）求y关于x的函数解析式，并写出它的定义域；

（3）当AP＝6 时，试比较∠CPN与∠A的大小，并说明理由．

18.如图，⊙O的半径为6，线段AB与⊙O相交于点C、D，AC＝4，∠BOD＝∠A，OB与⊙O相交于点E，设OA＝x，CD＝y．

（1）求BD的长；

（2）求y关于x的函数关系式，并写出定义域；

（3）当CE⊥OD时，求AO的长．

19.如图所示，AC⊥AB，AB＝2，AC＝2，点D是以AB为直径的半圆O上一动点，DE⊥CD交直线AB于点E，设∠DAB＝α（0°＜α ＜90°）．

（1）当α＝18°时，求的长；

（2）当α＝30°时，求线段BE的长；

（3）若要使点E在线段BA的延长线上，则α的取值范围是______________．（直接写出答案）

20.　如图，在四边形ABCD中，∠DAB＝∠ABC＝90°，CD与以AB为直径的半圆相切于点E，EF⊥AB于点F，EF交BD于点G．设AD＝a，BC＝b．

（1）求CD的长度（用a、b表示）；

（2）求EG的长度（用a、b表示）；

（3）试判断EG与FG是否相等，并说明理由．