

人教版 (五四制)七年级上册12.1 相交线获奖课件ppt
展开12.1.3同位角、内错角、同旁内角
教学目标: 1、理解三线八角中没有公共顶点的角的位置关系 ,知道什么是同位角、内错角、同旁内角.
2、通过比较、观察、掌握同位角、内错角、同旁内角的特征,能正确识别图形中的同位角、内错角和同旁内角.
重 点:掌握同位角、内错角、同旁内角的特征.
难 点:能在复杂图形中正确识别图形中的同位角、内错角和同旁内角.
教学过程:
一、问题情境:
前面我们研究了一条直线与另一条直线相交的
情形,现在我们进一步研究一条直线分别与两条直
线相交的情形.如图⑴,分别将木条,木条与木
条钉在一起,并把它们想象成两端可以无限延伸的
三条直线(即“直线,与直线相交” 也可以
说成“直线,被第三条直线所截” ).构成八
个角,其中没有公共顶点的角有什么位置关系?
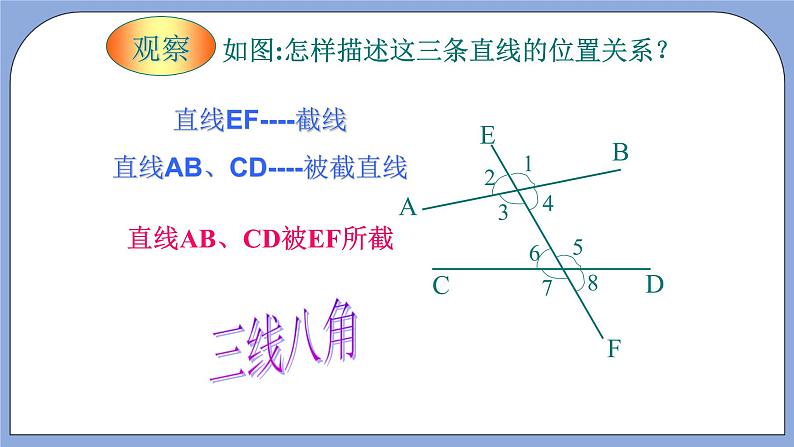
二、“三线八角”: 阅读课本“P6中”内容,完成下列问题:
1.操作:画两条直线AB,CD被第三条直线EF所截分别交AB,CD于点M,N,其中形成的小于平角的角共有8个.
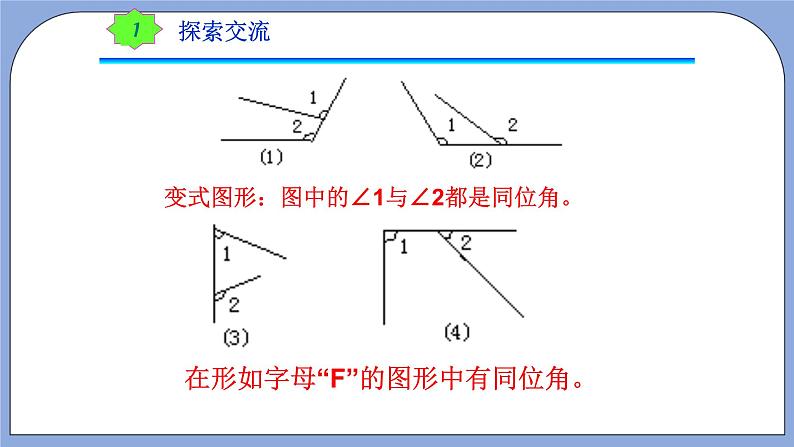
2.练习:如图⑴、⑵,其中∠1与∠2,∠3与∠4各是哪一条直线截哪两条直线而成的?
解:图⑴中∠1与∠2是直线AC截两条AB,CD得到的;
∠3与∠4是直线AB截两条AD,CB得到的;
图⑵中∠1与∠2是直线AB截两条DE,BC得到的;
∠3与∠4是直线DE截两条AB,AC得到的;
三、同位角、内错角、同旁内角:阅读课本“P6-P7上”内容,完成下列问题:
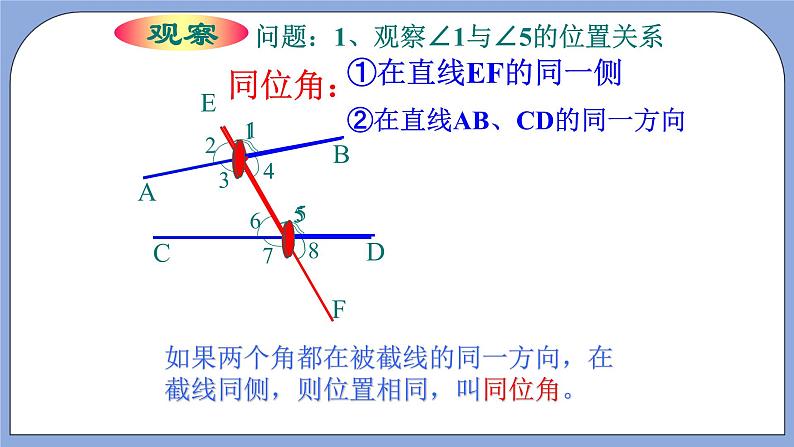
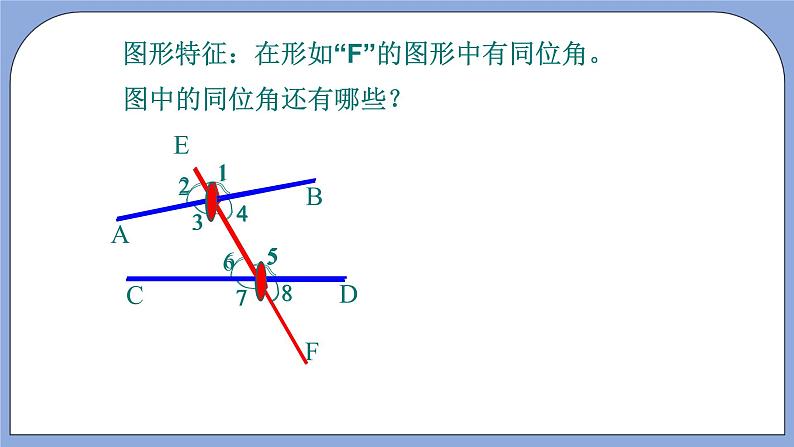
1. ⑴图⑶中∠1与∠5这对角在直线AB,CD,EF的什么位置?
同位角:在两被截线同旁,截线同侧,形如“F” 字型.
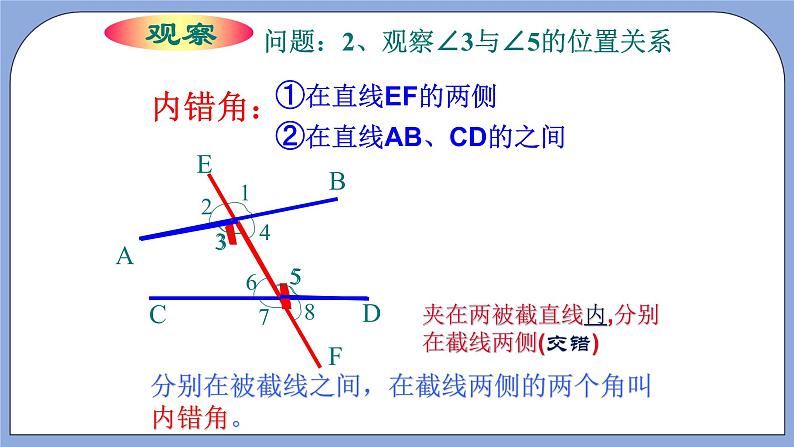
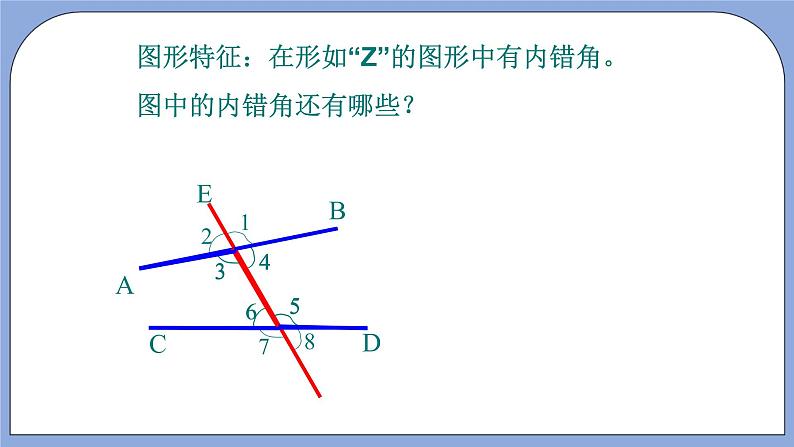
⑵图⑶∠3与∠5这对角在直线AB,CD,EF的什么位置?
内错角:在两被截线之间,截线两侧,形如“Z” 字型.
⑶图⑶∠4与∠5这对角在直线AB,CD,EF的什么位置?
同旁内角:在两被截线之间,截线同侧,形如“U” 字型.
2. 练习:⑴课本P43练习“1,2”
解:(略)
3. 讨论与交流:
指出图⑴、⑵中∠1,∠2,∠3,∠4与哪些角分别是同位角、内错角、同旁内角?
解:图⑴中∠1与∠2是内错角;∠3与∠4是内错角.
图⑵中∠1与∠2是同位角;∠3与∠4是同旁内角.
注意:本题要求指出图⑴、、⑵中∠1,∠2,∠3,∠4与哪些角分别是同位角、内错角、同旁内角,所以,将原图形分解为几个基本图形后,对于原图形中的线段或射线,不要给予延长,否则,将不属于原图形中的角.
四、课堂小结:
同位角:“F” 字型,“同旁同侧”
“三线八角” 内错角:“Z” 字型,“之间两侧”
同旁内角:“U” 字型,“之间同侧”
五、课堂检测:
⒈如图⑷,下列说法不正确的是( C )
A、∠1与∠2是同位角 B、∠2与∠3是同位角
C、∠1与∠3是同位角 D、∠1与∠4不是同位角
⒉如图⑸,直线AB、CD被直线EF所截,∠A和∠1 是同位角,∠A和∠3 是内错角,∠A和∠2 是同旁内角.
⒊如图⑹, 直线DE截AB, AC, 构成八个角:
① 指出图中所有的同位角、内错角、同旁内角.
②∠A与∠5, ∠A与∠6, ∠A与∠8, 分别是哪一条直线截哪两条直线而成的?
解:①图中所有的同位角有:∠1与∠8、∠2与∠5、∠3与∠6、∠4与∠7、
∠A与∠4、∠A与∠8.
图中所有的内错角有:∠2与∠A、∠3与∠8、∠4与∠5、∠6与∠A、
图中所有的同旁内角有:∠3与∠A、∠3与∠5、∠4与∠8、∠5与∠A、
②∠A与∠5, ∠A与∠6, ∠A与∠8都是直线AC截两条直线AB、DE而成的.
⒋如图⑺,在直角⊿ABC中,∠C=90°,DE⊥AC于E,交AB于D.
①指出当BC、DE被AB所截时,∠3的同位角、内错角和同旁内角.
②试说明∠1=∠2=∠3的理由.
解:①∠3的同位角是∠1,∠3的内错角是∠2,∠3的同旁内角是∠4.
②因为在直角⊿ABC中,∠C=90°,所以∠3+∠A=90°,
又因为DE⊥AC于E所以∠DEC=90°,⊿ADE是直角三角形,
所以∠1+∠A=90°,所以∠1=∠3,又因为∠1=∠2,
所以∠1=∠2=∠3.
六、课后作业
⒈书面作业:
⑴课本P45习题12.1“11”
如图,∠1与∠2,∠3与∠4各是哪一条直线截哪两条直线而成的?它们各是什么角?
解: 图⑴中∠1与∠2、∠3与∠4都是直线BD
截两条AB,CD得到的内错角;
图⑵中∠1与∠2是直线CB
截两条AB,CD得到的同旁内角;
∠3与∠4是直线AB
截两条AD,BC得到的同位角.
⒉跟踪训练:
⑴如图⑻,直线AB、CD被CD 所截,
则∠1和 ∠3 是同位角,
∠1和∠5 是内错角,
∠1和∠2 是同旁内角.
⑵如图⑼,指出∠1,∠2,∠3,
∠4,∠5中,是同位角的有2 对,
是内错角的有2 对,
是同旁内角的有3 对 .
⑶如图⑽,已知∠AOB=110°,
AO⊥OC,OB⊥OD,点O为垂足,
则∠AOD=20 °.
⑷如图⑾,OC⊥AB, OD⊥OE,
图中与∠1互余的角是 ∠DOC与∠EOB ,
若∠COD=60°,则∠AOE=120 °.
⑸在图⑿中,按要求画图:
①过点B画AC的垂线段;
②过点A画BC的垂线;
③画出表示点C到AB距离的线段.
解:如图示:
①过点B作BD⊥AC于D,
则线段BD就是所画的的垂线段;
② 过点A作AE⊥BC交CB的延长线于点E,
则直线AE就是所画的垂线;
③ 过点C作CF⊥AB于F,
则线段CF就是所画表示点C到AB距离的线段.
⑹如图⒀所示,AB是一条河流,要铺设管道将河水引到C、D两个用水点,现有两种铺设管道的方案:
方案一:分别过C、D作AB的垂线,垂足为E、F,沿CE、DF铺设管道;
方案二:连接CD交AB于点P,沿PC,PD铺设管道.
这两种铺设管道的方案哪一种更节省材料?为什么?
解:按方案一铺设管道更节省材料,理由如下:
因为CE⊥AB,DF⊥AB,而CD不垂直于AB,
根据“垂线段最短”,可知
CE<CP,DF<DP,所以CE+DF<CD,
所以沿CE,DF铺设管道更节省材料.
数学七年级下册5.1.3 同位角、内错角、同旁内角完整版课件ppt: 这是一份数学七年级下册5.1.3 同位角、内错角、同旁内角完整版课件ppt,共25页。PPT课件主要包含了CONTENTS,学习目标,知识回顾,新知探究,课堂小结,课堂练习,新课导入,探究新知,八个角,同一方上方等内容,欢迎下载使用。
初中数学华师大版七年级上册1 角教课内容课件ppt: 这是一份初中数学华师大版七年级上册1 角教课内容课件ppt,文件包含513同位角内错角同旁内角pptx、华东师大版中学数学七年级上第5章相交线与平行线513同位角内错角同旁内角教学详案docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
初中数学青岛版七年级下册9.1 同位角、内错角、同旁内角精品课件ppt: 这是一份初中数学青岛版七年级下册9.1 同位角、内错角、同旁内角精品课件ppt,文件包含91同位角内错角同旁内角课件pptx、91同位角内错角同旁内角教案docx等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。