专题1 三角恒等变换-高一数学下学期期末必考重点题型技法突破（人教A版）

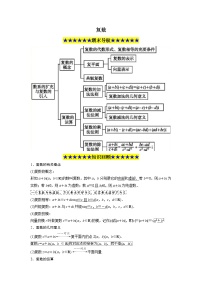
三角恒等变换

★★★★★★期末导航★★★★★★

★★★★★★知识回顾★★★★★★

1．两角和与差的余弦公式

C（α－β）：cos（α－β）＝cos αcos β＋sin αsin β ．

C（α＋β）：cos（α＋β）＝ cos αcos β－sin αsin β ．

2．两角和与差的正弦公式

S（α＋β）：sin（α＋β）＝sin αcos β＋cos αsin β ．

S（α－β）：sin（α－β）＝sin αcos β－cos αsin β ．

3．两角互余或互补

（1）若α＋β＝，其α、β为任意角，我们就称α、β互余．例如：－α与互余，＋α与互余．

（2）若α＋β＝π，其α，β为任意角，我们就称α、β互补．例如：＋α与互补，与－α互补．

4．两角和与差的正切公式

（1）T（α＋β）：tan（α＋β）＝  ．

（2）T（α－β）：tan（α－β）＝ ．

5．两角和与差的正切公式的变形

（1）T（α＋β）的变形：

tan α＋tan β＝tan（α＋β）（1－tan αtan β） ．

tan α＋tan β＋tan αtan βtan（α＋β）＝tan（α＋β） ．

tan α·tan β＝．

（2）T（α－β）的变形：

tan α－tan β＝tan（α－β）（1＋tan αtan β）  ．

tan α－tan β－tan αtan βtan（α－β）＝tan（α－β） ．

tan αtan β＝．

6.倍角公式及其变形形式

sin 2α＝2sinαcosα；

cos 2α＝cos2α-sin2α＝2cos 2α-1＝1-2sin2α ；

cos2α＝；

sin2α＝；

tan 2α＝

tan 2α＝＝（α≠kπ，k∈Z）．

关于两角差的余弦公式的三点说明

(1)公式的结构特点

公式的左边是差角的余弦，右边的式子是含有同名函数之积的和式，可用口诀“余余正正号相反”记忆公式．

(2)公式中的角α，β

公式中的角α，β不仅可以是角，而且可以是任意的整体，可以根据题目需要进行替换、变形代入，展开式仍然成立．

(3)公式的灵活应用

首先是公式的逆用，可以把符合公式特点的展开式合并，其次是角的灵活变化，如cos α＝cos[(α＋β)－β]．

两角和与差的正弦、余弦公式的记忆方法

(1)理顺公式间的联系．

C(α＋β)C(α－β)S(α－β)S(α＋β)

(2)注意公式的结构特征和符号规律．

对于公式C(α－β)，C(α＋β)，可记为“同名相乘，符号反”．

对于公式S(α－β)，S(α＋β)，可记为“异名相乘，符号同”．

两角和与差的正切

公式的结构特征及符号特征如下：

(1)公式T(α±β)的右侧为分式形式，其中分子为tan α与tan β 的和或差，分母为1与tan αtan β的差或和．

(2)

符号变化规律可简记为“分子同，分母反”．

3．两角和与差的正切公式的变形与特例

(1)变形公式：tan α＋tan β＝tan(α＋β)(1－tan α·tan β)；tan α－tan β＝tan(α－β)(1＋tan αtan β)；

tan αtan β＝1－.

(2)公式的特例：tan＝；

tan＝.

二倍角公式的理解

(1)对于“二倍角”应该广义地理解，如：8α是4α的二倍角，3α是α的二倍角，α是的二倍角，是的二倍角，…

(2)对于各个公式，要明确各公式成立的条件，其中sin 2α＝2sin αcos α，cos 2α＝cos2α－sin2α对任意角α都成立，而tan 2α的公式则具有局限性．

二倍角公式的应用

(1)二倍角公式的逆用：2sin αcos α＝sin 2α，sin αcos α＝sin 2α，cos α＝，cos2α－sin2α＝2cos2α－1＝1－2sin2α＝cos 2α，＝tan 2α.

(2)二倍角公式变形用：①升幂公式：1＋cos 2α＝2cos2α；1－cos 2α＝2sin2α，1＋cos α＝2cos2，1－cos α＝2sin2，1±sin 2α＝sin2α＋cos2α±2sin αcos α＝(sin α±cos α)2.

②降幂公式：cos2α＝，sin2α＝，(sin α±cos α)2＝1±sin 2α.

半角公式给出了求的正弦、余弦、正切的另一种方式，即只需知道cos α的值及相应α的条件，sin，cos，tan 便可求出．

由于tan＝及tan＝不含被开方数，且不涉及符号问题，所以求解题目时，使用相对方便，但需要注意该公式成立的条件．

asin x＋bcos x＝ sin(x＋θ)（其中）.

★★★★★★掌握题型★★★★★★

考点一 三角函数式的化简

【例1】 (1) 等于（   ）

A．    B．    C．    D．

【答案】A

【解析】原式．

（2）的结果是（   ）

A．1    B．    C．    D．

【答案】B

【解析】原式

．

【方法技巧】1.三角函数式的化简要遵循“三看”原则：一看角之间的差别与联系，把角进行合理的拆分，正确使用公式；二看函数名称之间的差异，确定使用的公式，常见的有“切化弦”；三看结构特征，找到变形的方向，常见的有“遇到分式要通分”、“遇到根式一般要升幂”等.

2.化简三角函数式的常见方法有弦切互化，异名化同名，异角化同角，降幂与升幂等.

【跟踪训练】

1.的值为（   ）

A．    B．    C．    D．

【答案】B

【解析】原式

．

2.的值是（   ）

A．     B．    C．    D．

【答案】B

【解析】

考点二 三角函数式的求值

【例2】(1) 的值是（   ）

A．    B．    C．    D．

【答案】C

【解析】

．

（2）计算的值等于（   ）

A．    B．    C．    D．

【答案】A

【解析】

．

【方法技巧】1.“给角求值”、“给值求值”问题求解的关键在于“变角”，使其角相同或具有某种关系，借助角之间的联系寻找转化方法.

2.“给值求角”：实质是转化为“给值求值”，先求角的某一函数值，再求角的范围，最后确定角.遵照以下原则：(1)已知正切函数值，选正切函数；(2)已知正、余弦函数值，选正弦或余弦函数；若角的范围是，选正、余弦皆可；若角的范围是(0，π)，选余弦较好；若角的范围为，选正弦较好.

【跟踪训练】

 1.(2022·合肥模拟) 已知，，求的值．

【解析】，       ①

．             ②

①式平方得，

②式平方得．

以上两式相加，有，

即，

得．

2.已知，，且，，求的值．

【解析】由题意易得，，

∴

．

考点三 三角恒等变换的简单应用

【例3】 (2022·郑州模拟) ．如图，点在以为直径的半圆上移动，且，过点作圆的切线，使．连接，当点在什么位置时，四边形的面积等于？

【解析】设，连接．

∵是直径，

∴．

又，

∴，．

∵是切线，

∴．

又,

∴

．

由已知，，

．又，

，

，．

故当点位于的中垂线与半圆的交点时，四边形的面积等于．

【方法技巧】1.进行三角恒等变换要抓住：变角、变函数名称、变结构，尤其是角之间的关系；注意公式的逆用和变形使用.

2.把形如y＝asin x＋bcos x化为y＝sin(x＋φ)，可进一步研究函数的周期、单调性、最值与对称性.

【跟踪训练】 (2020·北京卷) 求函数的单调区间．

【解析】．

当，即

，函数单调递增．

当，即

，函数单调递减．

因此原函数的单调递增区间是，

单调递减区间为．

★★★★★★题组训练★★★★★★

一、单选题

1．已知，则（       ）

A． B． C． D．

【答案】B

【解析】由题意可得：，

则：，，

从而有：，即.故选：B.

2．已知函数，则（       ）

A．的最小正周期为 B．的图象关于点对称

C．的最大值为 D．的图象关于直线对称

【答案】D

【解析】

对于选项，因为，故不正确；

对于选项，因为，故不正确；

对于选项，因为当时，，故不正确；

对于选项，因为，是的最大值，

所以的图象关于直线对称，故正确.故选：D.

3．已知，则的值为（       ）

A． B． C． D．

【答案】D

【解析】因为

，

所以，

故选：D

4．直线:与轴交于点，把绕点顺时针旋转得直线，的倾斜角为，则（   ）

A． B． C． D．

【答案】C

【解析】设的倾斜角为，则，，

由题意知，

．故选：C

5．若角α满足，则＝（　　）

A． B． C． D．

【答案】C

【解析】因为，可得，

两边平方，可得，

所以．故选：C.

6．若，，，，则

A． B． C． D．

【答案】D

【解析】，，则，，

，，

因此，.故选：D.

7．若是三角形的一个内角，且，则三角形的形状为（       ）

A．钝角三角形 B．锐角三角形

C．直角三角形 D．无法确定

【答案】A

【解析】∵，∴，

∵是三角形的一个内角，则，

∴，∴为钝角，∴这个三角形为钝角三角形.故选：A．

8．已知，，，均为锐角，则（       ）

A． B． C． D．

【答案】A

【解析】是锐角，，，

，，且，

，，

.故选：A

二、多选题

9．在中，若，则的形状（       ）

A．等腰三角形 B．直角三角形 C．等边三角形 D．锐角三角形

【答案】AB

【解析】，

.

.

，

或.

，，

，或.

为直角三角形或等腰三角形.故选：AB

10．设函数，则（       ）

A．的最小值为，其周期为

B．的最小值为，其周期为

C．在单调递增，其图象关于直线对称

D．在单调递减，其图象关于直线对称

【答案】AD

【解析】，函数的最小值是，周期，故A正确，B错误；

时，，所以在单调递减，令，得，其中一条对称轴是，故C错误，D正确.故选：AD

11．以下函数在区间上为单调增函数的有（       ）

A． B．

C． D．

【答案】BD

【解析】对于A选项，，当时，，

所以，函数在区间上不单调；

对于B选项，，当时，，

所以，函数在区间上单调递增；

对于C选项，，当时，，

所以，函数在区间上不单调；

对于D选项，当时，，所以，函数在区间上单调递增.故选：BD.

12．如图，一个水轮的半径为，水轮轴心距离水面的高度为，已知水轮按逆时针匀速转动，每分钟转动圈，当水轮上点从水中浮现时的起始（图中点）开始计时，记为点距离水面的高度关于时间的函数，则下列结论正确的是（       ）

A．

B．

C．若，则

D．不论为何值，是定值

【答案】BD

【解析】设，则，，则，

由题意可知，可得，

，可得，

由图可知，函数在附近单调递增，可得，

所以，.

对于A选项，，A错；

对于B选项，，，，B对；

对于C选项，由，可得，

所以，，解得，C错；

对于D选项，

，D对.故选：BD.

三、填空题

13．化简：＝________.

【答案】1

【解析】原式＝.故答案为：1

14．函数的最小值为___________．

【答案】.

【解析】，

，当时，，

故函数的最小值为．

15．函数，则的最小值为__________.

【答案】

【解析】因为，

所以当时，函数有最小值，最小值为，故答案为：.

16．在锐角△的内角A，B，C的对边分别为a，b，c,若，则的取值范围是______．

【答案】

【解析】由题设，，而，

所以，又，

所以，且△为锐角三角形，则，可得，

而.故答案为：

四、解答题

17．已知函数，，求的最值及取到最值时对应的x值．

【解析】设，则，∴，∴．

∵，∴，．

当，即时，．

此时，由，解得或，．

当，即时，．

此时，由，即．解得，．

综上，当或，时，取得最小值，；当，时，取得最大值，．

18．已知函数.

（1）求的最小正周期；

（2）当时，求的值域.

【解析】（1）

，

,

即的最小正周期为；

（2），，

，

，

的值域为.

19．已知函数，其中．

（1）若，是否存在实数使得函数为偶函数，若存在，求出的值；若不存在，请说明理由；

（2）若为函数的对称轴，求函数的单调增区间．

【解析】（1）当时，

若存在实数使得函数为偶函数，则恒成立，

即恒成立，

整理得恒成立，所以，与矛盾，

故不存在；

（2）结合三角函数的性质知，三角函数在对称轴处取最值，

又由辅助角公式知的最值为，

所以，

两边平方，得，所以，

即，所以，

所以，

当时，令，，

解得，，

所以单调增区间是，，

当时，令，，

解得，，

所以单调增区间是，．

20．已知函数，再从下列条件①、条件②这两个条件中选择一个作为已知.

条件①：的最大值与最小值之和为；条件②：.

(1)求的值；

(2)求函数在上的单调递增区间.

【解析】 (1)选①：

，

则，，

由已知可得，解得，此时.

选②：

，

，解得，此时.

(2)选①：由可得，

由，解得，故函数在上的单调递增区间为；

选②：同①.

21．（1）已知角的终边上有一点，求的值.

（2）已知，求的值.

【解析】（1）原式

因为知角的终边上有一点，根据任意角三角函数的定义可知：，

故原式.

（2）由，可得

，

，

又

.

22．已知函数的部分图象如图所示.

(1)求函数f（x）的解析式，并求出该函数的单调递增区间；

(2)若，且，求的值.

【解析】 (1)由图象可知，A=2， 且，解得

所以，

因为，

所以

则,

则仅当时，符合题意，

所以，

令，解得

综上，的解析式为，

单调增区间为；

(2)因为，

所以，

所以，又，

所以

所以.