2022-2023学年四川省泸县第四中学高二下学期开学考试数学（文）试题含解析

2022-2023学年四川省泸县第四中学高二下学期开学考试数学（文）试题

一、单选题

1．某校640名毕业生学生，现采用系统抽样方法，抽取32人做问卷调查，将640人按1，2，…，640随机编号，则抽取的32人中，编号落入区间[161,380]的人数为

A．10 B．11 C．12 D．13

【答案】B

【详解】使用系统抽样方法，从640人中抽取32人，即从20人抽取1人．

∴从编号161～380共220人中抽取 人．

故选B．

2．不等式的解集为（    ）

A． B．

C．或 D．或

【答案】A

【分析】先将分式不等式转化为一元二次不等式，然后求解即可

【详解】由，得，

解得，

所以原不等式的解集为，

故选：A

3．已知，则下列说法中一定正确的是（    ）

A． B． C． D．

【答案】B

【分析】AD选项，举出反例即可；BC选项，利用不等式的基本性质进行判断.

【详解】当，时，满足，此时，故A错误；因为，所以，，，B正确；因为，所以，，故，C错误；当，时，满足，，，所以，D错误.

故选：B

4．命题“所有奇数的立方都是奇数”的否定是（    ）

A．所有奇数的立方都不是奇数

B．存在一个奇数，它的立方是偶数

C．不存在一个奇数，它的立方是偶数

D．不存在一个奇数，它的立方是奇数

【答案】B

【分析】利用全称命题的否定解答即可.

【详解】由于命题“所有奇数的立方是奇数”是一个全称命题，

所以命题“所有奇数的立方是奇数”的否定是“存在一个奇数，它的立方是偶数”.

故选：B

5．某学校举办班级间篮球比赛，甲、乙两班得分情况如茎叶图所示，甲、乙两班得分的中位数分别是x甲，x乙，则下列说法正确的是（    ）

A．，甲比乙成绩稳定

B．，乙比甲成绩稳定

C．，甲比乙成绩稳定

D．，乙比甲成绩稳定

【答案】C

【分析】求出甲、乙两班得分的中位数，可比较x甲，x乙的大小，根据甲乙两班得分的分布情况，可判断其稳定性,

【详解】甲班得分情况从小到大排列为：，其中位数；

乙班得分情况从小到大排列为：，其中位数，

所以，

又因为乙的叶呈多峰；而甲的叶呈单峰，所以乙的方差比甲的大，所以甲比乙稳定．

故选：C．

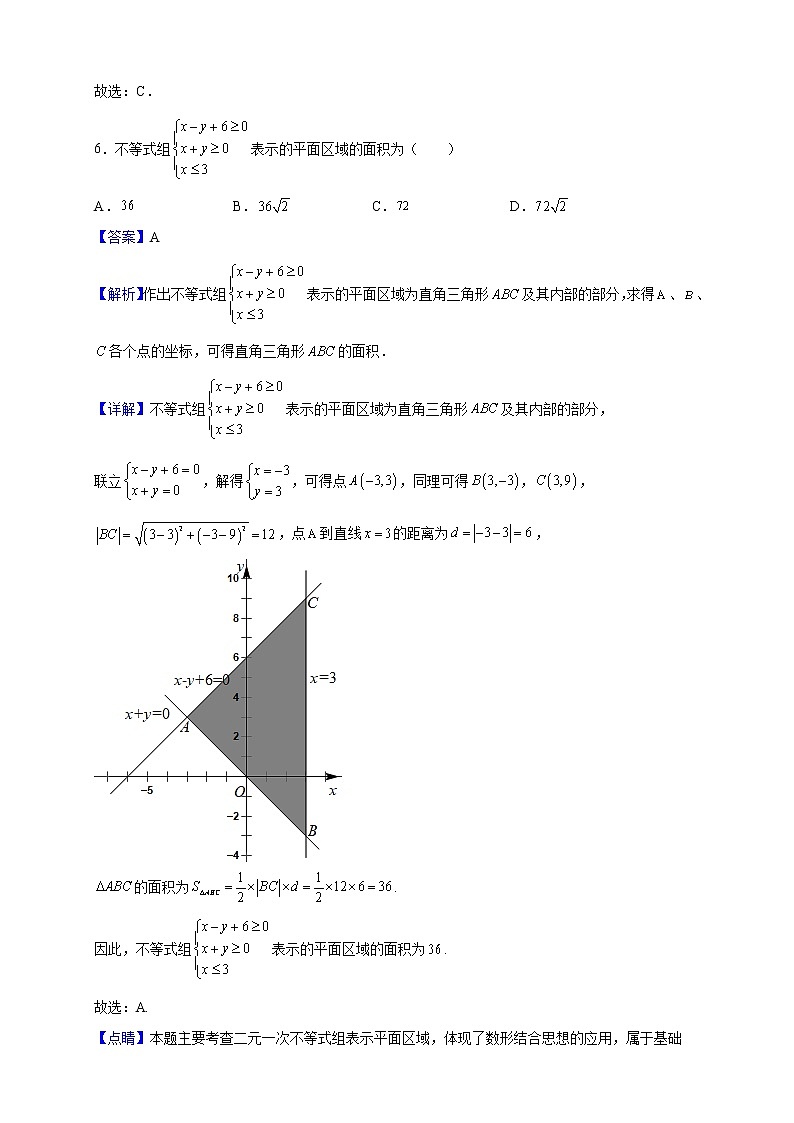
6．不等式组表示的平面区域的面积为（　　）

A． B． C． D．

【答案】A

【解析】作出不等式组表示的平面区域为直角三角形及其内部的部分，求得、、各个点的坐标，可得直角三角形的面积．

【详解】不等式组表示的平面区域为直角三角形及其内部的部分，

联立，解得，可得点，同理可得，，

，点到直线的距离为，

的面积为.

因此，不等式组表示的平面区域的面积为.

故选：A.

【点睛】本题主要考查二元一次不等式组表示平面区域，体现了数形结合思想的应用，属于基础题．

7．命题“，”为假命题，则的取值范围为（    ）

A． B．

C． D．

【答案】A

【分析】由于命题是假命题，可得其否定为真命题，然后可以建立关系即可求解.

【详解】命题“，”为假命题,

该命题的否定“，”为真命题，

即在上恒成立，

在单调递增，

，解得.

故选：A.

【点睛】本题考查根据命题的真假求参数范围，属于中档题.

8．已知圆过点，且圆心在直线上，则圆 的方程为

A． B．

C． D．

【答案】C

【分析】根据待定系数法求圆的方程.

【详解】设圆的方程为，由题意可得，解得，则圆的方程为.

故选：C.

9．焦点在轴上的椭圆的离心率是，则实数的值是（    ）

A． B． C． D．

【答案】A

【解析】由题意可得，则，再由离心率是，可得，从而可求出实数的值

【详解】解：由题意可得，则，

因为，所以，

所以，解得，

故选：A

10．已知实数，，且，则的最大值为（    ）

A． B． C． D．

【答案】B

【解析】由得：，，利用基本不等式即可求解.

【详解】由得：，

所以，

当且仅当即时等号成立，

所以的最大值为

故选：B

【点睛】本题主要考查了基本不等式求最值，属于中档题.

11．已知点为抛物线：上一点，且点到轴的距离比它到焦点的距离小3，则（    ）

A．3 B．6 C．8 D．12

【答案】B

【解析】由抛物线的定义可知点到焦点的距离等于它到准线的距离，可得，从而得出答案.

【详解】由题得，抛物线的准线方程为，

由抛物线的定义可知，点到焦点的距离等于它到准线的距离，

所以点到轴的距离比它到准线的距离小3，

于是得，所以．

故选：B

【点睛】本题考查抛物线的定义的应用，属于基础题.

12．已知抛物线的焦点为，准线与轴的交点为，为抛物线上一点，且在第一象限，当取得最小值时，点的坐标为（     ）

A． B． C． D．

【答案】B

【解析】过点作垂直于抛物线的准线，垂足为点，由抛物线的定义可得，可得出，结合图形可知，当直线与抛物线相切时，最大，则最小，设直线的方程为，将该直线方程与抛物线的方程联立，利用，求出方程组的解，即可得出点的坐标.

【详解】如下图所示：

过点作垂直于抛物线的准线，垂足为点，由抛物线的定义可得，

抛物线的准线为，则点，

由题意可知，轴，则，，

由图形可知，当直线与抛物线相切时，最大，则最小，

设直线的方程为，将该直线方程与抛物线的方程联立，

消去得，，，解得，则，

解得，此时，，因此，点的坐标为.

故选：B.

【点睛】本题考查根据抛物线上线段比的最值来求点的坐标，涉及抛物线定义的转化，解题的关键就是要抓住直线与抛物线相切这一位置关系来分析，考查数形结合思想的应用，属于中等题.

二、填空题

13．在定圆上随机取三点A、B、C，则是锐角三角形的概率等于______．

【答案】##0.25

【分析】根据题意，设对应的弧度数分别为，得到试验的全部结果构成事件：，再根据记“是锐角三角形”为事件，，作图，可得其概率的值.

【详解】设对应的弧度数分别为，

则试验的全部结果构成事件：，

记“是锐角三角形”为事件，则，如下图阴影部分，

结合图像，是锐角三角形的概率为.

故答案为：

14．已知M（4，2）是直线l被椭圆x2+4y2=36所截得的线段AB的中点，则直线l的方程为_____．

【答案】x+2y﹣8=0．

【详解】由题意得，斜率存在，设为 k，则直线l的方程为 y﹣2=k（x﹣4），即 kx﹣y+2﹣4k=0，

代入椭圆的方程化简得 （1+4k2）x2+（16k﹣32k2）x+64k2﹣64k﹣20=0，

∴x1+x2==8，解得 k=﹣，故直线l的方程为 x+2y﹣8=0，

故答案为： x+2y﹣8=0．

15．已知直线与曲线有两个不同的交点，则的取值范围是________．

【答案】

【分析】直线过定点，曲线表示圆心为原点，半径为2的圆的上半部分．画出图形，结合图形可得所求的范围．

【详解】由题意得，直线过定点，曲线表示圆心为原点，半径为2的圆的上半部分（包括与轴的交点），画出图形如下图所示．

当直线，即直线与圆相切时，

则有，解得，．

结合图形可得当直线与圆有两个不同的交点时，则有，

∴实数的取值范围是．

故答案为．

【点睛】解决曲线交点个数、方程根的个数等关于“个数”的问题时，一般要结合图形（或函数的图象）求解，即利用数形结合的方法求解，考查数形结合思想的运用和转化能力，属于中档题．

16．双曲线的左、右焦点分别为是左支上一点，且，直线与圆相切，则的离心率为__________．

【答案】

【详解】

设直线与圆相切于点 ，

则 ，

取的中点 ,连接 ，

由于,则 ，

由，

则，

即有，

由双曲线的定义可得，

即，即，

,即，，即，

则.故答案为.

三、解答题

17．已知圆心为的圆经过原点O.

（1）求圆C的方程；

（2）求与直线平行，且与圆C相切的直线方程.

【答案】（1）（2）

【分析】（1）由题意求出半径后即可得解；

（2）设直线方程为，利用直线与圆相切的性质列出方程即可得解.

【详解】（1）圆的半径为

从而圆的方程为

（2）设直线方程为，

圆心为，半径为，直线与圆相切，

∴圆心到直线的距离为

∴，，方程为

【点睛】本题考查了圆的方程的确定和直线与圆的位置关系，属于基础题.

18．某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：.

（1）求图中a的值；

（2）根据频率分布直方图，估计这100名学生语文成绩的平均数与中位数.

【答案】（1）（2）平均数为73，中位数为：.

【解析】（1）由频率和为1求解即可；

（2）以各区间中点值代表各组的取值,进而求得平均数；求出从左边开始小矩形的面积的和为0.5对应的横轴的值即为中位数

【详解】（1）由频率分布直方图知,

解得

（2）估计这100名学生语文成绩的平均分为:

由（1）,设中位数为,则

解得,故估计中位数为：.

【点睛】本题考查频率的性质,考查利用频率分布直方图求平均数和中位数,考查数据处理能力

19．已知函数，.

(1)若函数的图象关于直线对称，求实数的值，并写出函数的单调区间；

(2)解关于的不等式.

【答案】(1)；单调递增区间为，单调递减区间为

(2)答案见解析.

【分析】（1）利用二次函数的对称轴可求得；利用复合函数的单调性可求得 的单调区间；

（2）将化简为一元二次不等式，确定其对应方程的两根，并讨论两根的大小，从而确定不等式解集.

【详解】（1）由题意函数，，

由函数的图象关于直线对称，可得，则，

此时，定义域为，

在单调递增， 在单调递减，

故的递增区间为，单调递减区间为：.

（2）不等式即 化简为：，

对于，其图象抛物线开口向上，且有两根和，

①时，此时两根相等，则的解集为.

②时，此时，则不等式解集为.

③时，此时，则.

综上所述，当时，不等式的解集为；当时，不等式的解集为；

当时，不等式的解集为.

20．已知点，，动点满足：.

（1）求动点P的轨迹；

（2）已知点，若曲线E上一点M到x轴的距离为，求的值.

【答案】（1）焦点在x轴，开口向右的抛物线；（2）

【分析】（1）计算得到，化简得到答案.

（2）计算得到，再计算得到答案.

【详解】（1），，，

即：，点P的轨迹为焦点在x轴，开口向右的抛物线.

（2）由题意可得：代入方程求得.

.

【点睛】本题考查了轨迹方程，抛物线焦半径公式的应用，意在考查学生的应用能力和计算能力.

21．如图，在三棱锥中，已知△ABC和△PBC均为正三角形，D为BC的中点．

(1)求证：平面；

(2)若，，求三棱锥的体积．

【答案】(1)证明见解析；

(2).

【详解】（1）因为△ABC和△PBC为正三角形，D为BC的中点，

所以,

又,

所以平面

（2）因为△ABC和△PBC为正三角形，且，

所以,

又，

所以正三角形的面积为，

所以.

22．已知动圆过点 且动圆内切于定圆： 记动圆圆心的轨迹为曲线.

（1）求曲线的方程；

（2）若、是曲线上两点，点 满足 求直线的方程.

【答案】（1）；（2）.

【解析】（1）根据两圆内切，以及圆过定点列式求轨迹方程；（2）利用重心坐标公式可知，，再设直线的方程为与椭圆方程联立，利用根与系数的关系求解直线方程.

【详解】（1）由已知可得，两式相加可得 则点的轨迹是以 、 为焦点， 长轴长为的椭圆，则 因此曲线的方程是

(2)因为， 则点是的重心， 易得直线的斜率存在， 设直线的方程为，

联立 消 得：

且 ①

②

由①②解得 则直线的方程为 即

【点睛】本题考查直线与椭圆的问题关系，本题的关键是根据求得，.