

四川省泸县第四中学2023-2024学年高三文科数学上学期开学考试试题(Word版附解析)
展开
这是一份四川省泸县第四中学2023-2024学年高三文科数学上学期开学考试试题(Word版附解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
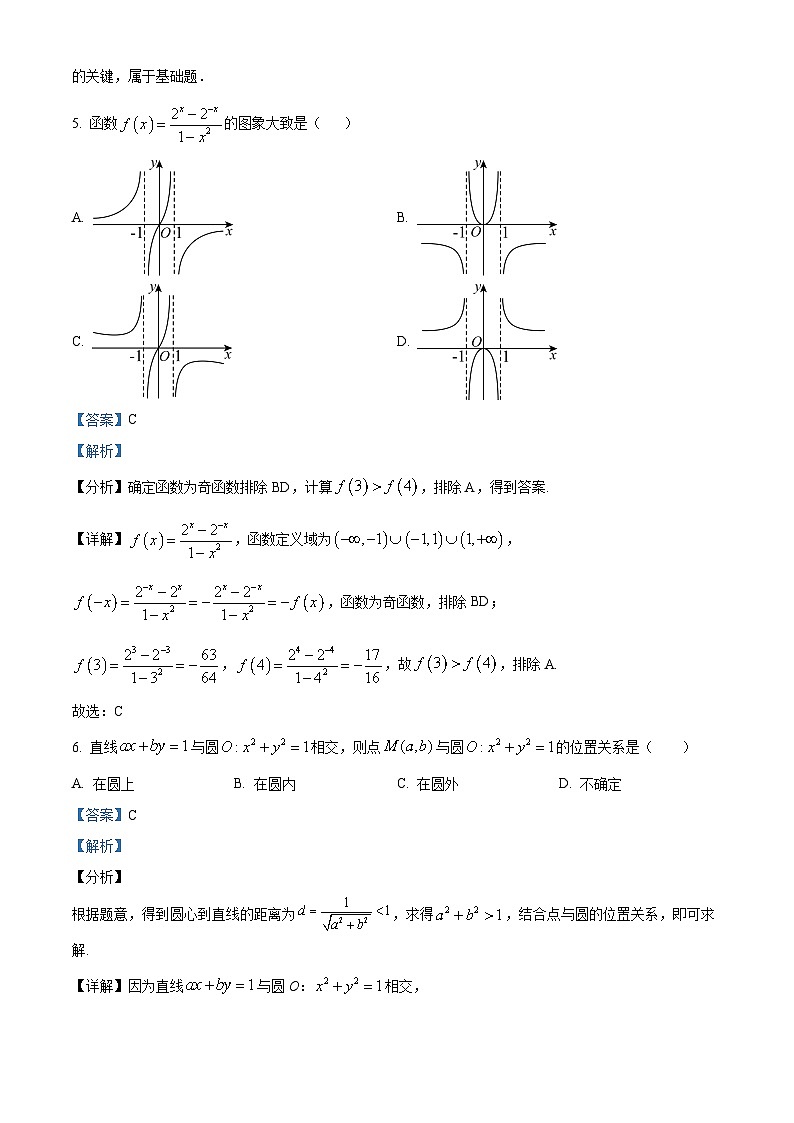
泸县四中高2021级高三上学期开学考试文科数学第I卷 选择题(60分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知复数,则( )A. B. C. D. 【答案】A【解析】【分析】利用复数的四则运算化简复数,根据共轭复数的定义可得出复数.【详解】由已知可得,因此,.故选:A.2. 已知一组数据的频率分布直方图如图所示,则数据的中位数估计值为( )A. 64 B. 65 C. 64.5 D. 66【答案】B【解析】【分析】首先判断中位数位于之间,设中位数为,依题意可得,解得即可.【详解】解:因为,所以中位数位于之间,设中位数为,则,解得,即中位数为.故选:B3. 成立的充要条件是( )A. B. C. D. 或【答案】D【解析】【分析】解分式不等式即可得解;【详解】解:因为,,,即,解得或,即,故成立的充要条件是“或”.故选:【点睛】本题考查分式不等式解法及充要条件的理解,属于基础题.4. 曲线在处的切线方程是( )A. B. C. D. 【答案】C【解析】【分析】求出函数的导数,可得切线的斜率,运用点斜式方程即可得到所求切线的方程.【详解】解:的导数为,可得在处的切线斜率为,切点为,即有在处的切线方程为,即为.故选:.【点睛】本题考查导数的运用:求切线的方程,考查导数的几何意义,正确求导和运用点斜式方程是解题的关键,属于基础题.5. 函数的图象大致是( )A. B. C. D. 【答案】C【解析】【分析】确定函数为奇函数排除BD,计算,排除A,得到答案.【详解】,函数定义域为,,函数为奇函数,排除BD;,,故,排除A.故选:C6. 直线与圆相交,则点与圆的位置关系是( )A. 在圆上 B. 在圆内 C. 在圆外 D. 不确定【答案】C【解析】【分析】根据题意,得到圆心到直线的距离为,求得,结合点与圆的位置关系,即可求解.【详解】因为直线与圆O:相交,可得圆心到直线的距离为,解得,所以点在圆外.故选:C.7. 很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以再加1;如果它是偶数,则将它除以;如此循环,最终都能够得到.下图为研究“角谷猜想”的一个程序框图.若输入的值为,则输出i的值为( )A. B. C. D. 【答案】B【解析】【分析】根据程序框图列举出程序的每一步,即可得出输出结果.【详解】输入,不成立,是偶数成立,则,;不成立,是偶数不成立,则,;不成立,是偶数成立,则,;不成立,是偶数成立,则,;不成立,是偶数成立,则,;不成立,是偶数成立,则,;成立,跳出循环,输出i的值为.故选:B.【点睛】本题考查利用程序框图计算输出结果,考查计算能力,属于基础题.8. 设为正数,若,则的最小值为( )A. 6 B. 9 C. 12 D. 15【答案】B【解析】【分析】直接利用基本不等式,结合已知代数式的形式进行求解即可.【详解】,,则,当且仅当,即时取等号.故选:B9. 经研究发现:某昆虫释放信息素t秒后,在距释放处x米地方测得信息素浓度y满足函数(A,K为非零常数).已知释放1秒后,在距释放处2米的地方测得信息素浓度为a,则释放信息素4秒后,信息素浓度为的位置距释放处的距离为( )米.A. B. 2 C. D. 4【答案】D【解析】【分析】根据已知数据可得,再根据即可求出值.【详解】由题知:当,时,,代入得:,当,时,,即,而,解得:或(舍)故选:D.10. 若,,,则( )A. B. C. D. 【答案】D【解析】【分析】用对数函数的单调性和比较,用指数函数的单调性和比较,用对数函数的单调性和比较,即可判断大小关系.【详解】因为,所以为减函数,所以,即因为,所以为增函数,所以,即.因为,所以为增函数,所以,即,所以.故选:D11. 在三棱柱中,,侧棱底面ABC,若该三棱柱的所有顶点都在同一个球O的表面上,且球O的表面积的最小值为,则该三棱柱的侧面积为( )A. B. C. D. 3【答案】B【解析】【详解】如图:设三棱柱上、下底面中心分别为、,则的中点为,设球的半径为,则,设,,则,,则在△中,,当且仅当时,等号成立,所以,所以,所以,所以该三棱柱的侧面积为.故选:B.【点睛】本题考查利用不等式求解棱柱的外接球面积最小值与侧面积问题,属于中档题12. 若函数在区间上有零点,则的最小值为( )A. B. C. D. 【答案】A【解析】【分析】设为函数的零点,则,转化为在直线上,根据表示点到原点的距离的平方,得到,构造新函数,利用导数求得函数的单调性与最值,即可求解.【详解】由题意,函数,设为函数在上的零点,则,即,即点在直线上,又表示点到原点的距离的平方,则,即,令,则,因为,所以,在单调递增.所以最小值为.故选:A【点睛】关键点点睛:设零点有,换主元化为点在直线上,结合的几何意义及点线距离公式得为关键.第II卷 非选择题(90分)二、填空题:本题共4小题,每小题5分,共20分.13. 已知向量,,且满足,则_______.【答案】4【解析】【分析】由向量垂直的坐标表示求解.【详解】由已知,又,所以,.故答案为:4.14. 若实数、满足,则目标函数的取值范围为______.【答案】【解析】【分析】画出约束条件的可行域,根据简单线性规划问题的解法,平移即可求解.【详解】作出图象,如图所示阴影区域为可行域:作直线的平行线,因为,越往上移,越大,越往下移,越小,当目标函数经过可行域的时,目标函数取得最大值2,目标函数经过时,目标函数取得最小值.所以目标函数的取值范围为.故答案为:.【点睛】本题考查简单线性规划问题的解法应用,准确画出可行域是解题的关键,属于基础题.15. 将某个圆锥体沿着母线和底面圆周剪开后展开,所得的平面图形是一个圆和扇形,已知该扇形的半径为,圆心角为,则圆锥的体积是_________.【答案】【解析】【分析】求得圆锥的底面半径和高,从而求得圆锥的体积.【详解】设圆锥的底面半径为,高为,则,,所以圆锥的体积为.故答案为:16. 已知双曲线的右焦点到的一条渐近线的距离为,则双曲线的方程为___________________.【答案】【解析】【分析】根据条件求出a,b,c即可.【详解】∵渐近线的方程为 , ,又 ,由点到直线的距离公式知: , ,∴双曲线C的方程为: ;故答案为: .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17. 为庆祝神舟十四号载人飞船返回舱成功着陆,某学校开展了航天知识竞赛活动,共有100人参加了这次竞赛,已知所有参赛学生的成绩均位于区间,将他们的成绩(满分100分)分成五组依次为,,,,,制成如图所示的频率分布直方图.(1)试估计这100人的竞赛成绩的平均数;(2)采用按比例分配的分层抽样的方法,从竞赛成绩在内的学生中随机抽取6人作为航天知识宣讲使者,再从第四组和第五组的使者中随机抽取2人作为组长,求这2人来自同一组的概率.【答案】(1)73.5 (2)【解析】【分析】(1)根据频率的性质求a,再根据平均数运算求解;(2)先根据分层抽样求每组抽取的人数,再结合古典概型运算求解.【小问1详解】依题意可得:,解得:,根据频率分布直方图知:每组的频率依次为,则平均数的估计值为,所以这100人的竞赛成绩的平均数的估计值为73.5.【小问2详解】由题意可知:竞赛成绩在,两个组的人数之比为,若采用分层抽样从中抽取6人,所以每组各抽学生人数分别为,分别记中所抽取的5人编号依次为1,2,3,4,5,中所抽取的1人编号为A,所以从6人中随机抽取2人的情况为:,,,,,,,,,,,,,,共15种结果,其中这2人来自同一组(记为事件)的有10种,则所以这2人来自不同组的概率为.18. 某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍薨”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,E、F、G分别是边长为4的正方形的三边的中点,先沿着虚线段将等腰直角三角形裁掉,再将剩下的五边形沿着线段折起,连接就得到了一个“刍甍”(如图2).(1)若O是四边形对角线的交点,求证:平面;(2)若,求三棱锥的体积.【答案】(1)证明见解析; (2).【解析】【分析】(1)线段中点为,证明即可;(2)利用等体积法求三棱锥的体积.【小问1详解】在图2中取线段中点H,连接,如图所示:由图1可知,四边形是矩形,且,∴O是线段与的中点,∴且,图1中且,而且.所以在图2中,且,∴且,∴四边形是平行四边形,则,由于平面,平面,∴平面.【小问2详解】∵,面,,∴面,,所以,即三棱锥的体积为.19. 高二理科班有60名同学参加某次考试,从中随机抽选出5名同学,他们的数学成绩与物理成绩如下表:数学成绩140130120110100物理成绩110901008070数据表明与之间有较强的线性关系.(Ⅰ)求关于的线性回归方程,并估计该班某同学的数学成绩为90分时该同学的物理成绩;(Ⅱ)本次考试中,规定数学成绩达到125分为数学优秀,物理成绩达到100分为物理优秀.若该班数学优秀率与物理优秀率分别为50%和60%,且所有同学中数学优秀但物理不优秀的同学共有6人,请你在答卷页上填写下面列联表,并判断能否在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关? 物理优秀物理不优秀合计数学优秀 数学不优秀 合计 参考公式及数据:回归直线的系数,,,,., .【答案】(Ⅰ),估计该班某同学的数学成绩为90分时该同学的物理成绩为63分;(Ⅱ)能在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关.【解析】【分析】(Ⅰ)由已知求得与的值,可得关于的线性回归方程,取求得值即可;(Ⅱ)由题意填写列联表,求得的值,结合临界值表得结论.【详解】解:(Ⅰ),.,.关于的线性回归方程为,取,得.估计该班某同学的数学成绩为90分时该同学的物理成绩为63分;(Ⅱ)由题意填写列联表: 物理优秀物理不优秀合计数学优秀24630数学不优秀121830合计362460,能在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关.【点睛】本题考查线性回归方程的求法,考查独立性检验,考查计算能力,属于中档题.20. 已知(1)若的单调递减区间是,求实数a的值(2)若,且对任意,都有,求实数a的取值范围【答案】(1) (2)【解析】【分析】(1)根据的单调递减区间是得到在上的解集为,然后求即可;(2)根据得到是上的递减函数,然后分和两种情况求解即可.【小问1详解】由题意得,则,因为的单调递减区间是,所以在上的解集为,所以,解得.【小问2详解】设,,令,则是上的递减函数,当时,,,函数是上的增函数,故,当时,,,函数是上增函数,故,所以实数的取值范围是.21. 已知椭圆C:的离心率,短轴长为.(1)求椭圆C的方程;(2)已知经过定点的直线l与椭圆相交于A,B两点,且与直线相交于点Q,如果,,那么是否为定值?若是,请求出具体数值;若不是,请说明理由.【答案】(1); (2).【解析】【分析】(1)由已知结合椭圆的性质可求a,b,进而可求椭圆方程;(2)先对直线l的斜率是否存在分类讨论,然后联立直线l与已知椭圆方程,结合方程的根与系数关系及向量的线性坐标表示可求.【小问1详解】由题意得,解得,,故椭圆C的方程为;【小问2详解】当直线l斜率不存在时,,,,,则,,,,此时,,;当直线l的斜率存在时,设斜率为k,则直线l的方程为,联立可得,设,,联立可得,则,,因为,,所以,,所以, 【点睛】圆锥曲线中的范围或最值以及定值问题,可根据题意构造关于参数的目标函数,然后根据题目中给出的范围或由判别式求解,解题中注意函数单调性和基本不等式的作用.另外在解析几何中还要注意向量的应用,如本题中根据向量的共线得到点的坐标之间的关系,进而为消去变量起到了重要的作用(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.(选修4-4 极坐标与参数方程)22. 在平面直角坐标系xOy中,设曲线的参数方程为(t为参数),以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,设曲线的极坐标方程为.(1)求曲线的普通方程;(2)若曲线上恰有三个点到曲线的距离为,求实数a的值.【答案】(1) (2)【解析】【分析】(1)曲线的参数方程消去参数即可求出曲线的普通方程;(2)首先曲线的极坐标方程转化为普通方程,可以得到曲线是圆,要使曲线上恰有三个点到曲线的距离为,圆心到直线的距离,求解方程即可.【小问1详解】由已知得代入,消去参数t得曲线的普通方程为.【小问2详解】由曲线的极坐标方程得,又,,,所以,即,所以曲线是圆心为,半径等于的圆.因为曲线上恰有三个点到曲线的距离为,所以圆心到直线的距离,即,解得.(选修4-5 不等式选讲)23. 已知,.(1)解不等式;(2)若方程有一个解,求实数的取值范围.【答案】(1);(2).【解析】【分析】(1)对分两种情况讨论,分别去掉绝对值符号,然后求解不等式组,再求并集即可得结果; (2).作出函数的图象, 当直线与函数的图象有一个公共点时,方程有一个解,由图可得结果.【详解】(1)不等式,即为.当时,即化为,得,此时不等式的解集为,当时,即化为,解得,此时不等式的解集为.综上,不等式的解集为.(2),即.作出函数的图象如图所示,当直线与函数的图象有一个公共点时,方程有一个解,所以或.所以实数取值范围是.
相关试卷
这是一份四川省泸州市泸县四中2023-2024学年高三下学期开学考试文科数学试题(Word版附解析),共16页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份四川省泸县第四中学2023-2024学年高三数学(理)上学期10月月考试题(Word版附解析),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份四川省泸县第四中学2023-2024学年高三上学期开学考试文科数学试题,共25页。









