广东省深圳市坪山区中山中学2022-2023学年七年级下学期3月月考数学试卷（含答案）

这是一份广东省深圳市坪山区中山中学2022-2023学年七年级下学期3月月考数学试卷（含答案），共11页。试卷主要包含了计算a2•a5的结果是，下列各式中，计算正确的是，计算，下列四个命题中，正确的是，有下列四种说法等内容，欢迎下载使用。

坪山区中山中学2022-2023学年第二学期七年级3月月考数学试卷

一．选择题（每题3分，共30分）
1．计算a2•a5的结果是（　　）
A．a10 B．a7 C．a3 D．a8
2．某种禽流感病毒变异后的直径为0.00000018米，0.00000018米用科学记数法表示为（　　）
A．1.8×10﹣5米 B．0.18×10﹣6米
C．1.8×10﹣7米 D．18×10﹣8米
3．下列各式中，计算正确的是（　　）
A．（x+1）（x﹣4）＝x2﹣4 B．（2m+3）2＝2m2+12m+9
C．（y+2）（y﹣3）＝y2﹣y﹣6 D．（5﹣2y）2＝25﹣4y2
4．下面的四个图形中，∠1与∠2是对顶角的是（　　）
A． B． C． D．
5．计算（﹣3）100×的结果是（　　）
A．﹣3 B．3 C． D．﹣
6．下列四个命题中，正确的是（　　）
A．经过直线外一点，有且只有一条直线与这条直线平行
B．同旁内角相等，两直线平行
C．相等的角是对顶角
D．若∠1+∠2+∠3＝180°，则∠1、∠2、∠3互补
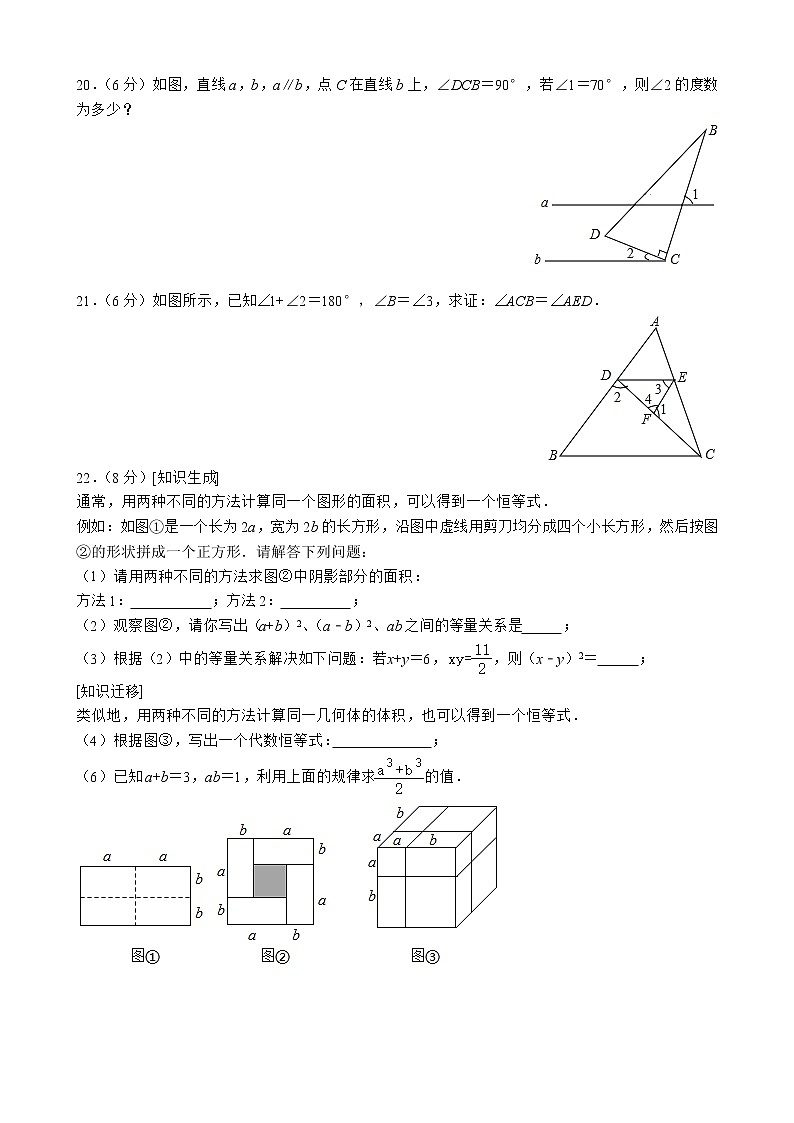
7．若一个角的补角是这个角余角的4倍，则这个角是（　　）
A．30° B．45° C．60° D．90°
8．已知a＝255，b＝344，c＝433，则a、b、c的大小关系为（　　）
A．a＞b＞c B．a＞c＞b C．b＞c＞a D．b＞a＞c
9．有下列四种说法：①锐角的补角一定是钝角；②一个角的补角一定大于这个角；③如果两个角是同一个角的补角，那么它们相等；④锐角和钝角互补．其中正确的是（　　）
A．①② B．①③ C．①②③ D．①②③④
10．如图，已知点C是线段AB上的一动点，分别以AC，BC为边向两边作正方形ACDE与正方形CFGB，若AB＝8，且两正方形的面积和为S1+S2＝36．则图中阴影部分的面积为（　　）

A．7 B．7.5 C．14 D．15
二．填空题（每题3分，共15分）
11．计算2a2b÷（﹣4ab）的结果是 　 　．
12．若2×8n×16n＝222，则n的值为　 　．
13．如图，直线a∥b，直线c与直线a，b分别交于点A，B．若∠1＝45°，则∠2＝　 　．

14．若多项式a2+ka+25是完全平方式，则k的值是　 　．
15．如图，一个宽度相等的纸条按如图所示方法折叠一下，则∠1＝　 　度．

三．解答题（共55分）
16．（16分）计算：
（1）（﹣1）2020+（﹣）﹣2﹣20210； （2）x3•x5﹣（2x4）2+x10÷x2；
（3）[（﹣xy2z）2﹣4x3y2z]÷x2y2； （4）（x+2y）（x﹣2y）﹣（x﹣y）2．



17．（7分）已知：如图∠AED＝∠C，∠DEF＝∠B，请你说明∠1与∠2相等吗？为什么？
解：因为∠AED＝∠C（已知）
所以　 　∥　 　（　 　）
所以∠B+∠BDE＝180° （　 　）
因为∠DEF＝∠B（已知）
所以∠DEF+∠BDE＝180° （　 　）
所以　 　∥　 　（　 　）
所以∠1＝∠2 （　 　）．

18．（6分）已知（am）n＝a6，（am）2÷an＝a3
（1）求mn和2m﹣n的值；
（2）求4m2+n2的值．



19．（6分）先化简后计算：（2x+1）（x﹣2）﹣（﹣3x+1）（﹣3x﹣1），其中x＝﹣2．


20．（6分）如图，直线a，b，a∥b，点C在直线b上，∠DCB＝90°，若∠1＝70°，则∠2的度数为多少？


21．（6分）如图所示，已知∠1+∠2＝180°，∠B＝∠3，求证：∠ACB＝∠AED．

22．（8分）[知识生成]
通常，用两种不同的方法计算同一个图形的面积，可以得到一个恒等式．
例如：如图①是一个长为2a，宽为2b的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的形状拼成一个正方形．请解答下列问题：
（1）请用两种不同的方法求图②中阴影部分的面积：
方法1：　 　；方法2：　 　；
（2）观察图②，请你写出（a+b）2、（a﹣b）2、ab之间的等量关系是　 　；
（3）根据（2）中的等量关系解决如下问题：若x+y＝6，，则（x﹣y）2＝　 　；
[知识迁移]
类似地，用两种不同的方法计算同一几何体的体积，也可以得到一个恒等式．
（4）根据图③，写出一个代数恒等式：　 　；
（6）已知a+b＝3，ab＝1，利用上面的规律求的值．


参考答案与试题解析
一．选择题
1．计算a2•a5的结果是（　　）
A．a10 B．a7 C．a3 D．a8
【解答】解：a2•a5＝a2+5＝a7，
故选：B．
2．某种禽流感病毒变异后的直径为0.00000018米，0.00000018米用科学记数法表示为（　　）
A．1.8×10﹣5米 B．0.18×10﹣6米
C．1.8×10﹣7米 D．18×10﹣8米
【解答】解：0.00000018＝1.8×10﹣7，
故选：C．
3．下列各式中，计算正确的是（　　）
A．（x+1）（x﹣4）＝x2﹣4 B．（2m+3）2＝2m2+12m+9
C．（y+2）（y﹣3）＝y2﹣y﹣6 D．（5﹣2y）2＝25﹣4y2
【解答】解：∵（x+1）（x﹣4）＝x2﹣3x﹣4，故选项A不合题意；
∵（2m+3）2＝4m2+12m+9，故选项B不合题意；
∵（y+2）（y﹣3）＝y2﹣y﹣6，故选项C符合题意；
∵（5﹣2y）2＝25﹣20y+4y2，故选项D不合题意；
故选：C．
4．下面的四个图形中，∠1与∠2是对顶角的是（　　）
A． B．
C． D．
【解答】解：根据对顶角的定义可知：只有C图中的∠1与∠2是对顶角，其它都不是．
故选：C．
5．计算（﹣3）100×的结果是（　　）
A．﹣3 B．3 C． D．﹣
【解答】解：原式＝（﹣3）100×（）100×
＝[（﹣3）×]100×
＝（﹣1）100×
＝．
故选：C．
6．下列四个命题中，正确的是（　　）
A．经过直线外一点，有且只有一条直线与这条直线平行
B．同旁内角相等，两直线平行
C．相等的角是对顶角
D．若∠1+∠2+∠3＝180°，则∠1、∠2、∠3互补
【解答】解：A、经过直线外一点，有且只有一条直线与这条直线平行，所以A选项符合题意；
B、同旁内角互补，两直线平行，所以B选项不符合题意；
C、相等的角不一定是对顶角，所以C选项不符合题意；
D、若∠1+∠2+∠3＝180°，∠1、∠2、∠3不互补，所以D选项不符合题意．
故选：A．
7．若一个角的补角是这个角余角的4倍，则这个角是（　　）
A．30° B．45° C．60° D．90°
【解答】解：设这个角为x°，则它的补角为（180﹣x）°，余角为（90﹣x）°，根据题意可得：
4（90﹣x）＝180﹣x，
解得：x＝60，
故选：C．
8．已知a＝255，b＝344，c＝433，则a、b、c的大小关系为（　　）
A．a＞b＞c B．a＞c＞b C．b＞c＞a D．b＞a＞c
【解答】解：∵a＝（25）11＝3211，b＝（34）11＝8111，c＝（43）11＝6411，
∴b＞c＞a．
故选：C．
9．有下列四种说法：
①锐角的补角一定是钝角；
②一个角的补角一定大于这个角；
③如果两个角是同一个角的补角，那么它们相等；
④锐角和钝角互补．
其中正确的是（　　）
A．①② B．①③ C．①②③ D．①②③④
【解答】解：①锐角的补角一定是钝角；根据补角的定义和钝角的定义可判断其正确性，故此选项正确；
②一个角的补角一定大于这个角；当这个角为钝角时，它的补角小于90°，故此选项错误；
③如果两个角是同一个角的补角，那么这两个角相等；利用同补角定义得出，此选项正确；
④中没有明确指出是什么角，故此选项错误．
故正确的有：①③，
故选：B．
10．如图，已知点C是线段AB上的一动点，分别以AC，BC为边向两边作正方形ACDE与正方形CFGB，若AB＝8，且两正方形的面积和为S1+S2＝36．则图中阴影部分的面积为（　　）

A．7 B．7.5 C．14 D．15
【解答】解：设AC＝a，BC＝b，则a+b＝8，
∵，
∴（a+b）2＝a2+b2+2ab＝36+2ab＝64，
∴ab＝14，
∴，
故选：A．
二．填空题
11．计算2a2b÷（﹣4ab）的结果是 　　．
【解答】解：原式＝a，
故答案为：a．
12．若2×8n×16n＝222，则n的值为　　．
【解答】解：2×8n×16n＝2×23n×24n＝21+3n+4n＝222，
∴1+3n+4n＝22，
解得：n＝3．
13．如图，直线a∥b，直线c与直线a，b分别交于点A，B．若∠1＝45°，则∠2＝　135°　．

【解答】解：∵直线a∥b，∠1＝45°，
∴∠3＝45°，
∴∠2＝180°﹣45°＝135°．
故答案为：135°．

14．若多项式a2+ka+25是完全平方式，则k的值是　±10　．
【解答】解：∵a2+ka+25是完全平方式，
∴ka＝±2×a×5，
∴k＝±10，
故答案为：±10．
15．如图，一个宽度相等的纸条按如图所示方法折叠一下，则∠1＝　65　度．

【解答】解：根据题意得2∠1与130°角相等，
即2∠1＝130°，
解得∠1＝65°．
故填65．
三．解答题
16．计算：
（1）（﹣1）2020+（﹣）﹣2﹣20210；
（2）x3•x5﹣（2x4）2+x10÷x2；
（3）[（﹣xy2z）2﹣4x3y2z]÷x2y2；
（4）（x+2y）（x﹣2y）﹣（x﹣y）2．
【解答】解：（1）原式＝1+9﹣1＝9；
（2）原式＝x8﹣4x8+x8＝﹣2x8；
（3）原式＝＝4y2z2﹣16xz；
（4）原式＝（x2﹣4y2）﹣（x2﹣2xy+y2）＝x2﹣4y2﹣x2+2xy﹣y2＝2xy﹣5y2．
17．已知：如图∠AED＝∠C，∠DEF＝∠B，请你说明∠1与∠2相等吗？为什么？
解：因为∠AED＝∠C（已知）
所以　DE　∥　BC　（　同位角相等，两直线平行　）
所以∠B+∠BDE＝180° （　两直线平行，同旁内角互补　）
因为∠DEF＝∠B（已知）
所以∠DEF+∠BDE＝180° （　等量代换　）
所以　EF　∥　AB　（　同旁内角互补，两直线平行，　）
所以∠1＝∠2 （　两直线平行，内错角相等　）．

【解答】解：因为∠AED＝∠C（已知）
所以 DE∥BC（ 同位角相等，两直线平行）
所以∠B+∠BDE＝180° （ 两直线平行，同旁内角互补）
因为∠DEF＝∠B（已知）
所以∠DEF+∠BDE＝180° （等量代换 ）
所以 EF∥AB（同旁内角互补，两直线平行 ）
所以∠1＝∠2 （ 两直线平行，内错角相等）．
故答案为：DE，BC，同位角相等，两直线平行，两直线平行，同旁内角互补，等量代换 EF，AB，同旁内角互补，两直线平行，两直线平行，内错角相等．
18．已知（am）n＝a6，（am）2÷an＝a3
（1）求mn和2m﹣n的值；
（2）求4m2+n2的值．
【解答】解：（1）∵（am）n＝a6，（am）2÷an＝a3，
∴amn＝a6、a2m﹣n＝a3，
则mn＝6、2m﹣n＝3；
（2）当mn＝6、2m﹣n＝3时，
4m2+n2＝（2m﹣n）2+4mn
＝32+4×6
＝9+24
＝33．
19．先化简后计算：（2x+1）（x﹣2）﹣（﹣3x+1）（﹣3x﹣1），其中x＝﹣2．
【解答】解：原式＝2x2﹣4x+x﹣2﹣9x2+1＝﹣7x2﹣3x﹣1，
当x＝﹣2时，原式＝﹣28+6﹣1＝﹣23．
20．如图，直线a，b，a∥b，点C在直线b上，∠DCB＝90°，若∠1＝70°，则∠2的度数为多少？

【解答】解：∵∠1＝70°，∠1与∠3是对顶角，
∴∠3＝∠1＝70°．
∵a∥b，点C在直线b上，∠DCB＝90°，
∴∠2+∠DCB+∠3＝180°，
∴∠2＝180°﹣∠3﹣∠DCB＝180°﹣70°﹣90°＝20°．

21．如图所示，已知∠1+∠2＝180°，∠B＝∠3，求证：∠ACB＝∠AED．

【解答】证明：∵∠1+∠2＝180°，∠1+∠4＝180°
∴∠2＝∠4，
∴BD∥EF（内错角相等、两直线平行）
∴∠3＝∠ADE（两直线平行，内错角相等）
∵∠B＝∠3
∴∠ADE＝∠B
∴DE∥BC（同位角相等、两直线平行）
∴∠ACB＝∠AED（两直线平行，同位角相等）．
22．[知识生成]
通常，用两种不同的方法计算同一个图形的面积，可以得到一个恒等式．
例如：如图①是一个长为2a，宽为2b的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的形状拼成一个正方形．请解答下列问题：
（1）请用两种不同的方法求图②中阴影部分的面积：
方法1：　（a﹣b）2　；方法2：　（a+b）2﹣4ab　；
（2）观察图②，请你写出（a+b）2、（a﹣b）2、ab之间的等量关系是　（a﹣b）2＝（a+b）2﹣4ab　；
（3）根据（2）中的等量关系解决如下问题：若x+y＝6，，则（x﹣y）2＝　14　；
[知识迁移]
类似地，用两种不同的方法计算同一几何体的体积，也可以得到一个恒等式．
（4）根据图③，写出一个代数恒等式：　（a+b）3＝a3+3a2b+3ab2+b3　；
（5）已知a+b＝3，ab＝1，利用上面的规律求的值．

【解答】解：（1）方法1，直接根据正方形的面积公式得，（a﹣b）2，
方法2，大正方形面积减去四种四个长方形的面积，即（a+b）2﹣4ab，
故答案为：（a﹣b）2，（a+b）2﹣4ab；
（2）故答案为：（a﹣b）2＝（a+b）2﹣4ab；
（3）由（2）得，（x﹣y）2＝（x+y）2﹣4xy＝36﹣22＝14；
故答案为：14；
（4）根据体积的不同计算方法可得；（a+b）3＝a3+3a2b+3ab2+b3；
故答案为：（a+b）3＝a3+3a2b+3ab2+b3；
（5）a+b＝3，ab＝1，
∴＝＝＝9．