辽宁省鞍山市千山区2022-2023学年九年级上学期期末数学试题(含答案)

初中阶段性教学成果评估

九年级数学学科试卷

一、选择题（每题3分，共24分）

1．－2的绝对值是（    ）

A．2 B． C． D．－2

2．在下列函数中y随x增大而减小的函数是（    ）

A．y＝5x B． C．y＝﹣2x D．

3．如图，是由棱长都相等的四个小正方体组成的几何体．该几何体的主视图是（    ）

A． B． C． D．

4．下列说法正确的是（    ）

A．了解一批灯泡的使用寿命采用全面调查

B．一组数据6，5，3，5，4的众数是5，中位数是3

C．“367人中必有2人的生日是同一天”是必然事件

D．一组数据10，11，12，9，8的平均数是10，方差是1.5

5．如图，正方形ABCD的两条对角线AC，BD相交于点O，点E在BD上，且BE＝CD，则∠BEC的度数为（    ）

A．22.5° B．60° C．67.5° D．75°

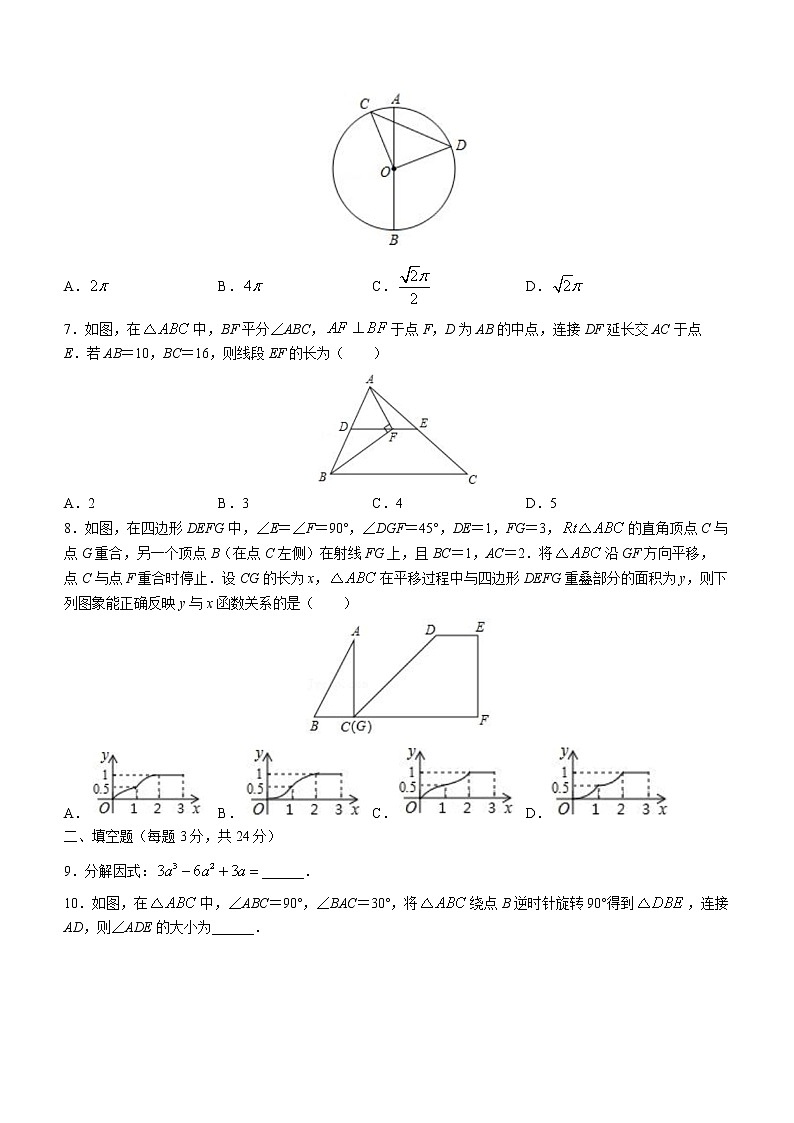
6．如图，AB是的直径，CD是弦，点C，D在直径AB的两侧．若，CD＝4，则的长为（    ）

A． B． C． D．

7．如图，在中，BF平分∠ABC，于点F，D为AB的中点，连接DF延长交AC于点E．若AB＝10，BC＝16，则线段EF的长为（    ）

A．2 B．3 C．4 D．5

8．如图，在四边形DEFG中，∠E＝∠F＝90°，∠DGF＝45°，DE＝1，FG＝3，的直角顶点C与点G重合，另一个顶点B（在点C左侧）在射线FG上，且BC＝1，AC＝2．将沿GF方向平移，点C与点F重合时停止．设CG的长为x，在平移过程中与四边形DEFG重叠部分的面积为y，则下列图象能正确反映y与x函数关系的是（    ）

A． B． C． D．

二、填空题（每题3分，共24分）

9．分解因式：______．

10．如图，在中，∠ABC＝90°，∠BAC＝30°，将绕点B逆时针旋转90°得到，连接AD，则∠ADE的大小为______．

11．设m、n是方程的两个实数根，则的值为______．

12．一种花瓣的花粉颗粒直径约为0.0000065米，将数据0.0000065用科学记数法表示为______．

13．如图，在矩形ABCD中，AB＝3，BC＝2，H是AB的中点，将沿CH折叠，点B落在矩形内点P处，连接AP，则______．

14．一副直角三角板，∠CAB＝∠FDE＝90°，∠F＝45°，∠C＝60°，按图中所示位置摆放，点D在边AB上，，则∠BDE的度数为______度．

15．如图，双曲线经过的对角线交点D，已知边OC在y轴上，且于点C，则的面积是______．

16．如图，点在直线y＝x上，过点分别作y轴、x轴的平行线交直线于点，，过点作y轴的平行线交直线y＝x于点，过点作x轴的平行线交直线于点，…，按照此规律进行下去，则点的横坐标为______．

三、解答题（共102分）

17．（8分）化简，再从－1，0，1中选择合适的x值代入求值．

18．（8分）如图，在中，点D，E分别是AB、AC边上的点，BD＝CE，∠ABE＝∠ACD，BE与CD相交于点F．求证：是等腰三角形．

19．（10分）为更好地践行社会主义核心价值观，让同学们珍惜粮食，学会感恩．校学生会积极倡导“光盘行动”，某天午餐后学生会干部随机调查了部分同学就餐饭菜的剩余情况，并将结果统计后绘制成如图所示的不完整的统计图．

（1）这次被调查的同学共有______名；

（2）补全条形统计图；

（3）计算在扇形统计图中剩一半饭菜所对应扇形圆心角的度数；

（4）校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供40人用餐．据此估算，全校2000名学生一餐浪费的食物可供多少人食用一餐？

20．（10分）小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯，已知两个陌生人到1至3层的任意一层出电梯，并设甲在a层出电梯，乙在b层出电梯．

（1）甲、乙二人在同一层楼出电梯的概率为______．

（2）小亮和小芳打赌说：“若甲、乙在同一层或相邻楼层出电梯，则小亮胜，否则小芳胜”．该游戏是否公平？并说明理由．

21．（10分）如图是一辆自卸式货车的示意图，矩形货厢ABCD的长AB＝4m．卸货时，货厢绕A点处的转轴旋转，货厢底部A、B两点在垂直方向上的距离与水平距离之比记作i．A点处的转轴与后车轮转轴（点M处）的水平距离叫做安全轴距，测得该车的安全轴距为0.7m．货厢对角线AC、BD的交点G可视为货厢的重心，测得∠ACB＝66.4°．假设该车在平地上进行卸货作业（即AN为水平线）．

（1）若，求A、B两点在垂直方向上的距离；

（2）卸货时发现，当A、G两点的水平距离小于安全轴距时，会发生车辆倾覆事故．若，该货车会发生上述事故吗？试说明你的理由．（参考数据：，，，）

22．（10分）如图，在平面直角坐标系中，一次函数y＝kx＋b的图象经过点，，交反比例函数的图象于点，点E是反比例函数图象上的一动点，横坐标为t（0＜t＜3），轴交直线AB于点F，D是y轴上任意一点，连接DE，DF．

（1）求一次函数和反比例函数的表达式；

（2）当t为何值时，是以EF为斜边的等腰直角三角形．

23．（10分）如图，AB为直径，C、D为上不同于A、B的两点，∠ABD＝2∠BAC，连接CD．过点C作，垂足为E，直线AB与CE相交于F点．

（1）求证：CF为的切线；

（2）当BF＝5，时，求BD的长．

24．（10分）某商店试销一款进价为60元/件的新童装，并与供货商约定，试销期间售价不低于进价，也不得高于进价的40%，同一周内售价不变．从试销记录看到，单价定为65元这周，销售了275件；单价定为75元这周，销售了225件．每周销量y（件）与销售单价x（元）符合一次函数关系．

（1）求每周销量y（件）与销售单价x（元）之间的关系式．

（2）商店将童装售价定为多少时，这周内销售童装获得毛利最大，最大毛利W是多少元？

（3）若商店规划一周内这项销售获得毛利不低于2500元，试确定售价x的范围．

25．（12分）

【证明体验】

（1）如图1，AD为的角平分线，∠ADC＝60°，点E在AB上，AE＝AC．求证：DE平分∠ADB．

【思考探究】

（2）如图2，在（1）的条件下，F为AB上一点，连结FC交AD于点G．若FB＝FC，DG＝2，CD＝3，求BD的长．

【拓展延伸】

（3）如图3，在四边形ABCD中，对角线AC平分∠BAD，∠BCA＝2∠DCA，点E在AC上，∠EDC＝∠ABC．若BC＝5，，AD＝2AE，求AC的长．

26．（14分）如图1，抛物线与x轴交于点A和点B，与y轴交于点C，直线y＝x＋4经过点A和点C．

（1）求抛物线的解析式；

（2）如图2，点P为y轴左侧抛物线上一动点，连CP、CB和AP．

①当点P在直线AC上方时，连PB交AC于D，记，求M的最大值及M取最大值时点P的坐标；

②当点P满足∠CBA－∠PCA＝45°时，请求出P点坐标．

千山区九年数学答案

一、选择题（共计24分）

1．A   2．C   3．D   4．C   5．C   6．D   7．B   8．B

二、填空题（共24分）

9．    10．15°   11．1000   12．    13．

14．15    15．3    16．

三、解答题（计102分）

17．（8分）

解：原式，

∵，∴x＝0，则原式＝﹣1．

18．（8分）

证明：∵∠ABE＝∠ACD，∴∠DBF＝∠ECF，在和中，

，∴，∴BF＝CF，DF＝EF，

∴∠FBC＝∠FCB，∴∠ABC＝∠ACB，∴AB＝AC，即是等腰三角形．

19．（8分）

解：（1）200；

（2）“剩少量”的人数：200﹣80﹣50﹣30＝40人，

补全条形统计图如图所示（语言叙述1分，补全图1分），

（3）“剩一半”的扇形圆心角是；

（4）（人），答：学生一餐浪费的食物约可供400人食用一餐．

20．（10分）

解：（1）

（2）该游戏不公平．理由：

由树状图可知，共有9种等可能的结果，其中两人在相邻楼层出电梯的结果有4种，

∴小亮获胜的概率为，小芳获胜的概率为，∵，∴该游戏不公平．

21．（10分）

解：（1）作，垂足为H，则∠AHB＝90°，∵，

∴，∴∠BAH＝30°，∴，

答：A、B两点在垂直方向上的距离为2m．

（2）不会发生上述事故，理由：

作，，垂足分别为J、K，

中，，

∠CAB＝90°﹣∠ACB＝90°﹣66.4°＝23.6°，∵，

∴∠FAE＝45°，∴∠CAJ＝45°＋23.6°＝68.6°，

中，，

∵，，∴∠AKG＝∠AJC，

又∵∠GAK＝∠CAJ，∴，∴，

∵四边形ABCD是矩形，∴GA＝GC，即，

∴，即，

故该货车不会发生上述事故．

22．（10分）

解：（1）把点A、B的坐标代入一次函数表达式得：，解得，

∴一次函数表达式为；

把点C的坐标代入上式得：，故点C的坐标为，

将点C的坐标代入反比例函数表达式得：，

故反比例函数表达式为；

（2）设点E的坐标为，则点，

当∠FDE为直角时，如下图，

过点D作于点H，∵为等腰直角三角形，故，

即，解得（舍去），．

23．（10分）

（1）证明：连接OC．∵OA＝OC，∴∠1＝∠2．

又∵∠3＝∠1＋∠2，∴∠3＝2∠1．又∵∠4＝2∠1，∴∠4＝∠3，

∴．∵，∴．

又∵OC为的半径，∴CF为的切线；

（2）连接AD．在中，∵∠BEF＝90°，BF＝5，，

∴．∵，∴，∴．

设的半径为r，∴，∴．

∵AB为直径，∴AB＝15，∠ADB＝90°，∵∠4＝∠EBF，∴∠F＝∠BAD，

∴，∴，∴BD＝9．

24．（10分）

解：（1）设y与x之间的关系式为，

由题意得：，解得：，∴所求关系式为．

（2）设商店将童装售价定为x元，．

∴当x＜90时，W随x的增大而增大．而最大售价为60×（1＋40%）＝84（元）．

∴当x＝84时，．

∴当售价定为84元时，一周内获得毛利最大，最大毛利是4320元．

（3）由，得，

解得，．结合（2）知，．

25．（12分）

解：（1）证明：如图1，∵AD平分∠BAC，∴∠EAD＝∠CAD，

∵AE＝AC，AD＝AD，∴，∴∠ADE＝∠ADC＝60°，

∵∠BDE＝180°－∠ADE－∠ADC＝180°－60°－60°＝60°，

∴∠BDE＝∠ADE，∴DE平分∠ADB．

（2）如图2，∵FB＝FC，∴∠EBD＝∠GCD；

∵∠BDE＝∠CDG＝60°，∴，∴；

∵，∴DE＝CD＝3，∵DG＝2，∴．

（3）如图3，在AB上取一点F，使AF＝AD，连结CF．

∵AC平分∠BAD，∴∠FAC＝∠DAC，∵AC＝AC，

∴，∴CF＝CD，∠FCA＝∠DCA，∠AFC＝∠ADC，

∵∠FCA＋∠BCF＝∠BCA＝2∠DCA，∴∠DCA＝∠BCF，即∠DCE＝∠BCF，

∵∠EDC＝∠ABC，即∠EDC＝∠FBC，∴，∴，∠DEC＝∠BFC，

∵BC＝5，，∴；

∵∠AED＋∠DEC＝180°，∠AFC＋∠BFC＝180°，∴∠AED＝∠AFC＝∠ADC，

∵∠EAD＝∠DAC（公共角），∴，

∴，∴AC＝2AD，AD＝2AE，∴．

26．（14分）

解：（1）直线y＝x＋4经过点A和点C，

当x＝0时，y＝4当y＝0时，x＝﹣4，∴，，

∵抛物线与x轴交于点A和点B，与y轴交于点C，

∴，解得，∴抛物线的解析式为．

（2）①过点P作轴，垂足为E，∵抛物线的解析式为，

当y＝0时，，解得x＝1或x＝﹣4，∴，

∴，，∴AO＝4，CO＝4，BO＝1．

设，∴，OE＝﹣x，

∵

，

∵，．

∴，

∴当时，M有最大值，此时．

②根据题意可知，OA＝OC＝4，∴∠OAC＝∠OCA＝45°．

需要分两种情况：

当点P在直线AC上方时，设直线CP交x轴于点K，

∵∠CBA﹣∠PCA＝45°，∴∠CBA＝45°＋∠PCA＝∠OCK，

∴，∴，即，

∴OK＝16，即．∴直线CP的解析式为：，

令，解得x＝0（舍去）或，∴；

当点P在直线AC下方时，设直线交x轴于点G，

∵，∴，∴CG＝CB，

∴点O是BG的中点，∴，∴直线的解析式为：y＝4x＋4，

令，解得x＝0（舍去）或x＝﹣7，∴．

综上，点P的坐标为：或．