高中数学北师大版 (2019)必修 第二册4.2 平面向量及运算的坐标表示备课课件ppt

这是一份高中数学北师大版 (2019)必修 第二册4.2 平面向量及运算的坐标表示备课课件ppt，共25页。PPT课件主要包含了自主预习·新知导学，合作探究·释疑解惑，易错辨析，探究一，探究二，答案D，答案A等内容，欢迎下载使用。

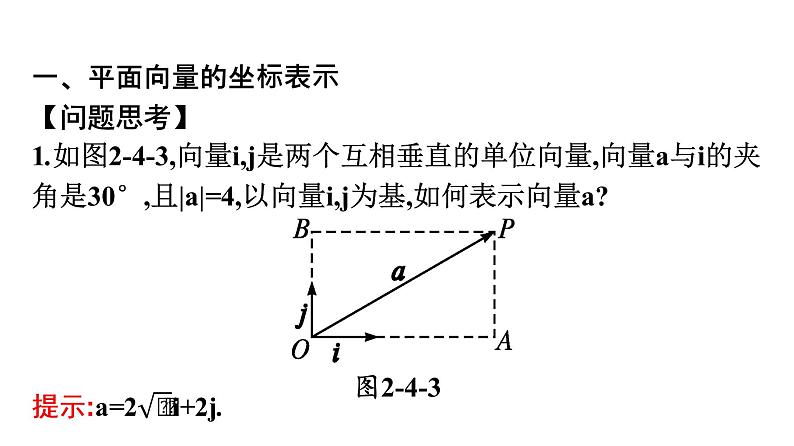
一、平面向量的坐标表示【问题思考】1.如图2-4-3,向量i,j是两个互相垂直的单位向量,向量a与i的夹角是30°,且|a|=4,以向量i,j为基,如何表示向量a?
2.在平面直角坐标系内,给定点A的坐标为(1,1),则点A的位置确定了吗?给定向量a的坐标为(1,1),则向量a的位置确定了吗?提示:对于点A,若给定A的坐标为(1,1),则点A的位置确定.对于向量a,给定a的坐标为(1,1),此时给出了a的方向和大小,但因向量的位置由起点和终点确定,且向量可以任意平移,因此a的位置不确定.
4.想一想:相等向量的坐标相同吗?相等向量的起点、终点的坐标一定相同吗?提示:由向量坐标的定义知,相等向量的坐标一定相同,但是相等向量的起点、终点的坐标可以不同.
二、平面向量运算的坐标表示【问题思考】1.设i,j是分别与x轴、y轴同向的两个单位向量,若设a=(x1,y1),b=(x2,y2),则a=x1i+y1j,b=x2i+y2j,根据向量的线性运算性质,向量a+b,a-b,λa(λ∈R)如何分别用基i,j表示?提示:a+b=(x1+x2)i+(y1+y2)j,a-b=(x1-x2)i+(y1-y2)j,λa=λx1i+λy1j.
2.(1)平面向量的坐标运算①运算法则:已知a=(x1,y1),b=(x2,y2)和实数λ,那么a+b=(x1+x2,y1+y2),a-b=(x1-x2,y1-y2),a=λ(x1,y1)=(λx1,λy1).②语言叙述:两个向量和与差的坐标分别等于这两个向量相应坐标的和与差;实数与向量数乘的坐标等于这个实数与向量的相应坐标的乘积.
3.若向量a=(2,3),b=(-1,2),则a-b的坐标为(　　).A.(1,5)B.(1,1)C.(3,1)D.(3,5)答案:C
提示:(1)①中b=2a,②中b=-3a,③中b=-a.(2)共线.(3)坐标不为(0,0)时成比例.
2.在平面直角坐标系中,a=(x1,y1),b=(x2,y2),b≠0,则向量a,b共线的充要条件是 x1y2-x2y1=0.3.想一想:如果两个非零向量共线,那么你能通过其坐标判断它们是同向还是反向吗?提示:能.将b写成λa的形式,当λ>0时,b与a同向,当λ<0时,b与a反向.
分析:(1)可直接运用坐标运算法则进行计算;(2)应先求出相关向量的坐标,再运用法则计算.
反思感悟 平面向量坐标运算的技巧:(1)若已知向量的坐标,则直接应用两个向量和、差及向量数乘的运算法则进行.(2)若已知有向线段两端点的坐标,则可先求出向量的坐标,再进行向量的坐标运算.(3)向量的线性坐标运算可完全类比数的运算进行.
【例2】 已知向量a=(1,2),b=(λ,1),若(a+2b)∥(2a-2b),则λ的值等于(　　).
本例条件不变,若a+b与4b-2a平行,则实数λ的值是　　　　　. 解析:因为a=(1,2),b=(λ,1),所以a+b=(1+λ,3),4b-2a=(4λ-2,0).由a+b与4b-2a平行,得3(4λ-2)-0=0,解得λ= . 
反思感悟 根据向量共线条件求参数问题,一般有两种思路,一是利用向量共线定理a=λb(b≠0),列方程组求解,二是利用向量共线的坐标表达式x1y2-x2y1=0求解.
处理向量共线时,忽视零向量的特殊情况致误【典例】 已知a=(3,2-m)与b=(m,-m)平行,求m的值.
以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?提示:本题中,当m=0时,b=0,显然a∥b成立.利用坐标比例形式判断向量共线的前提是m·(-m)≠0,错解中漏掉了m=0这种情况.正解:∵a∥b,∴3(-m)-(2-m)m=0,解得m=0或m=5.