2022年山东省烟台市、枣庄市高考数学适应性试卷（一）

这是一份2022年山东省烟台市、枣庄市高考数学适应性试卷（一），共18页。试卷主要包含了已知点F1、F2分别为椭圆C，下列结论正确的有，84，则P=0等内容，欢迎下载使用。


2022年山东省烟台市、枣庄市高考数学适应性试卷（一）

1.（5分）已知集合A={-2,-1,1,2}，B={x|2x<1}，则A∩B=()
A. {-2,-1} B. {1,2}
C. {-2,-1,1} D. {-2,-1,2}
2.（5分）若复数z满足(1-i)z=1+2i，则- z在复平面内对应的点位于(    )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.（5分）若圆锥的母线长为2，侧面积为2π，则其体积为()
A. 6π B. 3π C. 63π D. 33π
4.（5分）二进制在计算机技术中应用广泛．一二进制数以2为基数，通常用0和1两个数码来表示，进位规则是从最右面的数位依次向左满二进一，如二进制数101对应的十进制数为1×22+0×21+1×20=5.那么，十进制数22对应的二进制数为()
A. 10011 B. 10101 C. 10110 D. 11010
5.（5分）曲线y=x3+bx2+c在点M(1,0)处的切线与直线x-y-2=0垂直，则c的值为()
A. -1 B. 0 C. 1 D. 2
6.（5分）在(x2-2x+y)6的展开式中，含x5y2项的系数为()
A. -480 B. 480 C. -240 D. 240
7.（5分）声音是山物体振动产生的．我们平时听到的声音几乎都是复合音．复合音的产生是由于发音体不仅全段在振动，它的各部分如二分之一、三分之一、四分之一等也同时在振动．不同的振动的混合作用决定了声音的音色，人们以此分辨不同的声音．已知刻画某声音的函数为y=sinx+12sin2x+13sin3x，则其部分图象大致为()
A.
B.
C.
D.
8.（5分）已知点F1、F2分别为椭圆C：x2a2+y2b2=1(a>b>0)的左、右焦点，点P为直线x=a2b上一个动点．若tan∠F1PF2的最大值为33，则椭圆C的离心率为()
A. 34 B. 33 C. 24 D. 22
9.（5分）下列结论正确的有()
A. 若随机变量ξ，η满足η=2ξ+1，则D(η)=2D(ξ)+1
B. 若随机变量ξ～N(3,σ2)，且P(ξ<6)=0.84，则P(3<ξ<6)=0.34
C. 若样本数据(xi,yi)(i=1,2,3,…，n)线性相关，则用最小二乘估计得到的经验回归直线经过该组数据的中心点(x-,y-)
D. 根据分类变量X与Y的成对样本数据，计算得到χ2=4.712.依据α=0.05的独立性检验(x0.05=3.841)，可判断X与Y有关且犯错误的概率不超过0.05
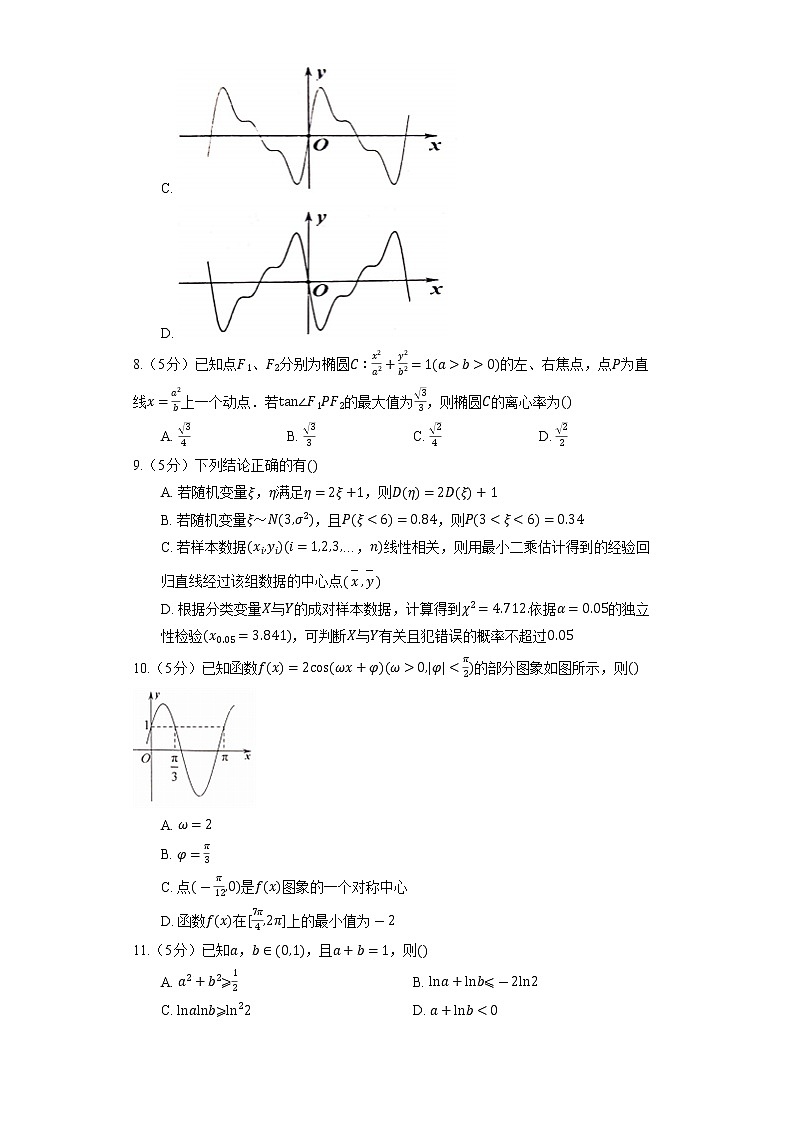
10.（5分）已知函数f(x)=2cos(ωx+φ)(ω>0,|φ|<π2)的部分图象如图所示，则()

A. ω=2
B. φ=π3
C. 点(-π12,0)是f(x)图象的一个对称中心
D. 函数f(x)在[7π4,2π]上的最小值为-2
11.（5分）已知a，b∈(0,1)，且a+b=1，则()
A. a2+b2⩾12 B. lna+lnb⩽-2ln2
C. lnalnb⩾ln22 D. a+lnb<0
12.（5分）给出构造数列的一种方法：在数列的每相邻两项之间插入此两项的和，形成新的数列，再把所得数列按照同样的方法不断构造出新的数列．现自1，1起进行构造，第1次得到数列1，2，1，第2次得到数列1，3，2，3，1，…，第n(n∈N*)次得到数列1，x1，x2，…，xk，1，记an=1+x1+x2+…+xk+1，数列{an}的前n项和为Sn，则()
A. a4=81 B. an=3an-1-1
C. an=3n+1 D. Sn=12×3n+1+n-32
13.（5分）已知α为锐角，且sinα=34，则cos(π-α)的值为 ______.
14.（5分）已知函数f(x+1)为偶函数，当x∈(0,1)时，f(x)=2-x，则f(log23)的值为 ______.
15.（5分）已知a→,b→均为单位向量，且夹角为π3，若向量c→满足(c→-2a→)·(c→-b→)=0，则|c→|的最大值为 ______.
16.（5分）鲁班锁是我国传统的智力玩具，起源于中国古代建筑中的榫卯结构，其内部的凹凸部分啮合十分精巧．图1是一种鲁班锁玩具，图2是其直观图．它的表面山八个正三角形和六个正八边形构成，其中每条棱长均为2.若该玩具可以在一个正方体内任意转动(忽略摩擦)，则此正方体表面积的最小值为 ______.

17.（12分）已知正项数列{an}的前n项和为Sn，且4，an+1，Sn成等比数列，其中n∈N*. 
(1)求数列{an}的通项公式； 
(2)设bn=4Snanan+1，求数列{bn}的前n项和Tn.
18.（12分）在△ABC中，角A，B，C的对边分别为a，b，c，且acosC+3asinC=b+c. 
(1)求A； 
(2)若b=3，c=2，角A的平分线交BC于M，求AM的长．
19.（12分）如图，在平行六面体ABCD-A1B1C1D1中，A1D⊥底面ABCD，AB=AA1=2AD=2，∠DAB=60°. 
(1)证明：AD⊥A1B； 
(2)设点P为线段DC1上一点(异于D，C1)，当DP为何值时，面A1PB与面AA1D1D夹角的余弦值最大？

20.（12分）2020年以来，新冠疫情对商品线下零售影响很大．某商家决定借助线上平台开展销售活动．现有甲、乙两个平台供选择，且当每件商品的售价为a(300⩽a⩽500)元时，从该商品在两个平台所有销售数据中各随机抽取100天的日销售量统计如下，
商品日销售量(单位：件)
6
7
8
9
10
甲平台的天数
14
26
26
24
10
乙平台的天数
10
25
35
20
10
假设该商品在两个平台日销售量的概率与表格中相应日销售量的频率相等，且每天的销售量互不影响． 
(1)求“甲平台日销售量不低于8件”的概率，并计算“从甲平台所有销售数据中随机抽取3天的日销售量，其中至少有2天日销售量不低于8件”的概率； 
(2)已知甲平台的收费方案为：每天佣金60元，且每销售一件商品，平台收费30元；乙平台的收费方案为：每天不收取佣金，但采用分段收费，即每天销售商品不超过8件的部分，每件收费40元，超过8件的部分，每件收费35元．某商家决定在两个平台中选择一个长期合作，从日销售收入(单价×口销售量-平台费用)的期望值较大的角度，你认为该商家应如何决策？说明理由．
21.（12分）已知双曲线C：x2a2-y2b2=1(a>0,b>0)的实轴长为2.点(7,-1)是抛物线E：x2=2py的准线与C的一个交点． 
(1)求双曲线C和抛物线E的方程； 
(2)过双曲线C上一点P作抛物线E的切线，切点分别为A，B.求△PAB面积的取值范围．
22.（12分）已知函数f(x)=ae2x-x2，a∈R. 
(1)设f(x)的导函数为g(x)，讨论g(x)零点的个数； 
(2)设f(x)的极值点为x1，x2(x1
答案和解析
1.【答案】A
【解析】解：A={-2,-1,1,2}，B={x|2x<1}={x|x<0}， 
∴A∩B={-2,-1}， 
故选：A. 
先求出集合B，再利用集合的交集运算求解． 
此题主要考查了交集及其运算，属于基础题．

2.【答案】C
【解析】解：由(1-i)z=1+2i，得z=1+2i1-i=(1+2i)(1+i)(1-i)(1+i)=-12+32i， 
∴- z=-1 2-3 2i， 
则- z在复平面内对应的点的坐标为(-1 2,-3 2)，位于第三象限． 
故选：C． 
把已知等式变形，利用复数代数形式的乘除运算化简，然后求出- z的坐标得答案． 
该题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础题．

3.【答案】D
【解析】解：设圆锥的底面半径为r，高为h， 
则πr×2=2π，可得r=1， 
则h=22-r2=3， 
因此，该圆锥的体积为V=13πr2h=13π×12×3=33π. 
故选：D. 
计算出圆锥的底面半径和高，利用锥体的体积公式可求得该圆锥的体积． 
此题主要考查了圆锥的体积计算，属于基础题．

4.【答案】C
【解析】解：∵1×24+0×23+1×22+1×21+0×20=22， 
∴十进制数22对应的二进制数为10110. 
故选：C. 
根据二进数的定义，结合题中的例子进行求解． 
此题主要考查二进制的运算，考查十进制与二进制的互化等基础知识，考查运算求解能力，是基础题．

5.【答案】C
【解析】解：设f(x)=x3+bx2+c，则f'(x)=3x2+2bx，直线x-y-2=0的斜率为1， 
由题意可得{f'(1)=3+2b=-1f(1)=b+c+1=0，解得{b=-2c=1. 
故选：C. 
由已知条件列出方程组，求解方程组即可解得c的值． 
此题主要考查导数的几何意义，属于基础题．

6.【答案】A
【解析】解：(x2-2x+y)6的展开式中，含x5y2的项为C61x2·C53(-2x)3·C22y2=-480x5y2， 
∴含x5y2项的系数为-480， 
故选：A. 
利用二项式定理求解． 
此题主要考查了二项式定理，属于基础题．

7.【答案】C
【解析】解：令y=f(x)=sinx+12sin2x+13sin3x， 
求导得f'(x)=cosx+cos2x+cos3x=cosx+cos2x+cos2xcosx-sin2xsinx 
=cosx(1-2sin2x)+cos2x(1+cosx)=(1+2cosx)cos2x， 
所以，当x∈(0,π4)时，f'(x)>0，函数f(x)单调递增， 
当x∈(π4,π2)时，f'(x)<0，函数f(x)单调递减， 
当x∈(π2,2π3)时，f'(x)<0，函数f(x)单调递减， 
当x∈(2π3,3π4)时，f'(x)>0，函数f(x)单调递增， 
当x∈(3π4,π)时，f'(x)<0，函数f(x)单调递减， 
由于f(0)=0,f(π4)=223+12,f(2π3)=34,f(3π4)=223-12>0,f(π)=0， 
所以，x∈(0,π)时，f(x)>0，且单调区间变化不具有对称的性质， 
所以，只有C选项满足． 
故选：C. 
令y=f(x)=sinx+12sin2x+13sin3x，进而求导得f'(x)=(1+2cosx)cos2x，再讨论x∈(0,π)时，f'(x)的符号得f(x)的单调区间与函数值的符号，进而得答案． 
此题主要考查了函数的图象的变换，属于中档题．

8.【答案】D
【解析】解：根据对称性，不妨设点P在第一象限且坐标为(a2b,m)(m>0)，如图， 
记直线x=a2b与x轴的交点为M， 
设∠F2PM=α，∠F1PM=β，则∠F1PF2=β-α， 
由于F1(-c,0)，F2(c,0)， 
故|MF1|=a2b+c,|MF2|=a2b-c， 
所以，tanα=a2b-cm,tanβ=a2b+cm， 
所以tan∠F1PF2=tan(β-α)=2cm1+(a2b)2-c2m2=2mcb2m2b2+a4-b2c2=2cb2mb2+a4-b2c2m， 
因为m>0,mb2+a4-b2c2m⩾2b2(a4-b2c2)，当且仅当mb2=a4-b2c2m时等号成立， 
即m2=a4-b2c2b2时等号成立， 
所以tan∠F1PF2=2cb2mb2+a4-b2c2m⩽2cb22b2(a4-b2c2)=33， 
整理得4c4-4a2c2+a4=0， 
所以4e4-4e2+1=0，解得e2=12， 
所以e=22，即椭圆C的离心率为22. 
故选：D. 
根据对称性，不妨设点P在第一象限且坐标为(a2b,m)(m>0)，设∠F2PM=α，∠F1PM=β，则∠F1PF2=β-α，进而结合正切的差角公式和基本不等式可得4c4-4a2c2+a4=0，进而根据齐次式求离心率即可． 
此题主要考查了椭圆的离心率的求解计算，属于中档题．


9.【答案】BCD
【解析】解：对A，由方差的性质可知，若随机变量ξ，η满足η=2ξ+1，则D(η)=22D(ζ)=4D(ζ)，故错误； 
对B，根据正态分布的图象对称性可得P(3<ξ<6)=P(ξ<6)-0.5=0.34，故B正确； 
对C，根据回归直线过样本中心点可知C正确； 
对D，由χ2=4.712>3.841可知判断X与Y有关且犯错误的概率不超过0.05，故D正确． 
故选：BCD. 
对A，根据方差的性质判断即可； 
对B，根据正态分布的对称性判断即可； 
对C，根据回归直线的性质判断即可； 
对D，根据独立性检验的性质判断即可． 
此题主要考查了方差，正态分布和回归直线与独立性检验的性质，属于基础题．

10.【答案】AC
【解析】解：对AB选项，令f(x)=2cos(ωx+φ)=1，得cos(ωx+φ)=12，如右图，根据f(x)的图象及y=cosx的图象可得： 
(πω+φ)-(πω3+φ)=5π3-π3，∴2ω3=4π3，∴ω=2，故选项A正确； 
又ω×0+φ=-π3+2kπ，k∈Z，又|φ|<π2，∴φ=-π3，故选项B错误； 
∴f(x)=2cos(2x-π3)， 
对C选项，∵f(-π12)=2cos(-π2)=0，∴点(-π12,0)是f(x)图象的一个对称中心，故选项C正确； 
对D选项，∵周期T=2πω=2π2=π，f(x)在[7π4,2π]上的最小值即为f(x)在[-π4,0]上的最小值， 
又当x∈[-π4,0]时，2x-π3∈[-5π6,-π3]，∴cos(2x-π3)的最小值为cos(-5π6)=-32，∴f(x)的最小值为-3，故选项D错误， 
 故选：AC. 
根据f(x)图象，结合y=cosx的图象，三角函数图象性质可求解f(x)的解析式，再根据解析式可对各个选项判断． 
此题主要考查三角函数的图像性质，数形结合思想，属中档题．


11.【答案】ABD
【解析】解：对于A：∵1=(a+b)2=a2+b2+2ab⩽2(a2+b2)， 
∴a2+b2⩾12，当且仅当a=b=12时等号成立，故A正确， 
对于B：由基本不等式可得ab⩽(a+b2)2=14，当且仅当a=b=12时等号成立， 
∴lna+lnb=lnab⩽ln14=-2ln2，故B正确， 
对于C：取a=14，b=34，则lnalnb-ln22=ln14ln34-ln22=-2ln2ln34-ln22=ln2(ln169-ln2)<0， 
此时lnalnb 对于D：令f(x)=1-x+lnx，其中0 则f'(x)=1x-1=1-xx>0，∴f(x)在(0,1)上单调递增， 
∵0 故选：ABD. 
利用基本不等式可判断A，利用基本不等式结合对数函数的单调性可判断B，利用特殊值法可判断C，构造函数f(x)=1-x+lnx，利用函数在(0,1)上的单调性可判断D. 
此题主要考查了基本不等式的应用，考查了构造函数的数学思想，属于中档题．

12.【答案】CD
【解析】解：由题意得：a1=4，a2=10=3×4-2，a3=28=3×10-2，a4=82=3×28-2，所以有an=3an-1-2，因此选项AB不正确； 
an=3an-1-2⇒an-1=3(an-1-1)， 
所以数列{an-1}是以a1-1=3为首项，3为公比的等比数列， 
因此有an-1=3⋅3n-1=3n⇒an=3n+1，因此选项C正确； 
Sn=3(1-3n)1-3+n=12×3n+1+n-32，所以选项D正确， 
故选：CD. 
通过计算求出a1，a2，a3，a4的值，运用归纳法得到an，an-1之间的关系，最后根据等比数列的定义和前n项和公式进行求解判断即可． 
此题主要考查了根据递推式证明等比数列以及数列的求和问题，属于中档题．

13.【答案】 -74
【解析】解：因为α为锐角，且sinα=34， 
所以cosα=1-sin2α=74， 
所以cos(π-α)=-cosα=-74， 
故答案为：-74. 
利用正余弦的同角公式求出cosα，再根据诱导公式化简即可求解． 
此题主要考查了诱导公式的应用，考查了学生的运算能力，属于基础题．

14.【答案】 34
【解析】解：根据题意，函数f(x+1)为偶函数，则函数f(x)关于直线x=1对称， 
则f(log23)=f(2-log23)=f(log243)， 
又由0 则f(log23)=34， 
故答案为：34. 
根据题意，分析可得函数f(x)关于直线x=1对称，由此可得f(log23)=f(2-log23)=f(log243)，结合函数的解析式计算可得答案． 
此题主要考查函数奇偶性性质以及应用，涉及函数值的计算，属于基础题．

15.【答案】 7+32
【解析】 
解：建立如图所示的平面直角坐标系， 
设向量b→，2a→，c→在平面直角坐标系对应的点为B，D，C， 
由a→,b→均为单位向量，且夹角为π3， 
则B(12,32)， 
又OD→=2a→， 
则D(2,0)， 
由(c→-2a→)·(c→-b→)=0， 
即点C的轨迹为以BD为直径的圆， 
则圆心E(54,34)，半径R=AB2=(2-12)2+(0-32)22=32， 
则|c→|的最大值为OE+R=(54)2+(34)2+32=7+32， 
故答案为：7+32. 
先建立如图所示的平面直角坐标系，设向量b→，2a→，c→在平面直角坐标系对应的点为B，D，C，由(c→-2a→)·(c→-b→)=0，即点C的轨迹为以BD为直径的圆，最后结合圆的性质求解即可． 
此题主要考查了平面向量数量积及轨迹问题，重点考查了向量模的问题，属中档题．


16.【答案】 168+962
【解析】解：将鲁班锁补成正方体ABCD-A1B1C1D1，然后以点A为坐标原点， 
AB、AD、AA1所在直线分别为x、y，z轴建立如下图所示的空间直角坐标系， 
 
在鲁班锁所在几何体上任取一个顶点P(0,2,2+22)， 
观察图形可知，P到鲁班锁所在几何体上其他顶点的距离的最大值在|PE|、|PF|、|PG|、|PH|、|PM|、|PN|、|PR|、|PS|中取得， 
结合图形可知E(2,0,0)、F(2+2,0,0)、G(2+22,2,0)、H(2+22,2+2,0)、 
M(2+2,2+22,0)、N(2,2+22,0)、R(0,2+2,0)、S(0,2,0)， 
则|PE|2=4+(2+22)2=16+82,|PF|2=(2+2)2+2+(2+22)2=20+122， 
|PG|2=2(2+22)2=24+162,|PH|2=2(2+22)2+4=28+162， 
|PM|2=(2+22)2+2×(2+2)2=24+162， 
|PN|2=2+(2+2)2+(2+22)2=20+122， 
|PR|2=4+(2+22)2=16+82,|PS|2=(2+22)2=12+82， 
所以，P到鲁班锁所在几何体上其他顶点的距离的最大值28+162， 
所以，若该玩具可以在一个正方体内任意转动(忽略摩擦)， 
设该正方体的棱长的最小值为a，则a=28+162， 
该正方体的表面积为S=6a2=168+962. 
故答案为：168+962. 
计算出该玩具任意两点间最大距离，可得出正方体的棱长，即可求得正方体的表面积． 
此题主要考查了立体几何的综合应用，属于中档题．

17.【答案】（1）解：对任意的n∈N*，an＞0，由题意可得4Sn=(an+1)2=an2+2an+1， 
当n=1时，则4a1=4S1=a12+2a1+1，解得a1=1， 
当n≥2时，由4Sn=an2+2an+1可得4Sn-1=an-12+2an-1+1， 
上述两个等式作差得4an=an2-an-12+2an-2an-1， 
即（an+an-1）（an-an-1-2）=0， 
因为an+an-1＞0， 
所以，an-an-1=2， 
所以，数列{an}为等差数列，且首项为1，公差为2， 
则an=1+2（n-1）=2n-1； 
（2）Sn=n(1+2n-1)2=n2， 
则bn=4Snanan+1=4n2(2n-1)(2n+1)=4n2-1+1(2n-1)(2n+1)=1+1(2n-1)(2n+1)=1+12(12n-1-12n+1)， 
因此，Tn=n+12(1-13+13-15+⋯+12n-1-12n+1)=n+n2n+1．
【解析】 
(1)由已知可得4Sn=an2+2an+1，令n=1可求得a1的值，令n⩾2，由4Sn=an2+2an+1可得4Sn-1=an-12+2an-1+1，两式作差推导出数列{an}为等差数列，确定该数列的首项和公差，利用等差数列的通项公式可求得{an}的通项公式； 
(2)求出Sn，可求得bn=1+12(12n-1-12n+1)，利用分组求和法结合裂项相消法可求得Tn. 
此题主要考查了数列的递推关系以及裂项相消求和，属于中档题．

18.【答案】解：（1）△ABC中，且acosC+3asinC=b+c， 
利用正弦定理：sinAcosC+3sinAsinC=sinB+sinC， 
整理得sinAcosC+3sinAsinC=sin（A+C）+sinC， 
故3sinA=cosA+1， 
整理得sin（A-π6）=12， 
由于0＜A＜π，所以A=π3； 
（2）在△ABC中，由余弦定理得a2=32+22-2×3×2cosπ3=7，即a=7， 
所以cosB=a2+c2-b22ac=7+4-92×7×2=714，所以sinB=32114， 
设△ABC边BC上的高为h， 
所以S△ABM=12AB•AM•sinA2=12BM•h，S△ACM=12AC•AM12CM•h， 
所以BMMC=ABAC=23，所以BM=275， 
所以在△ABM中，由正弦定理得BMsin∠BAM=AMsinB，即275×2=14·AM321， 
所以AM=635．
【解析】 
(1)直接利用正弦定理和三角函数的关系式的变换的应用求出A的值； 
(2)利用余弦定理可得a，进而可得cosB，设△ABC边BC上的高为h，可得BM=275，由正弦定理可得AM. 
此题主要考查的知识要点：三角函数的关系式的变换，正弦定理余弦定理和三角形面积公式的应用，主要考查学生的运算能力和数学思维能力，属于中档题．

19.【答案】解：（1）证明：连接BD，∵AB=2AD=2，∠DAB=60°， 
∴在△ABD中，由余弦定理得： 
BD2=AB2+AD2-2AB•AD•cos∠DAB=5-4cos60°=3，∴BD=3， 
∴AD2+BD2=AB2，∴AD⊥BD， 
∵A1D⊥底面ABCD，∴A1D⊥AD， 
∵A1D∩BD=D，∴AD⊥平面A1BD，∴AD⊥A1B； 
（2）结合（1）可知DA，DA1，DB两两垂直，以D为坐标原点，建立空间直角坐标系， 
则D（0，0，0），A（1，0，0），A1（0，0，3），B（0，3，0），C（-1，3，0）， 
∴DC1→=DA1→+A1B1→+B1C1→=DA1→+AB→+BC→=（0，0，3）+（-1，3，0）+（-1，0，0）=（-2，3，3）， 
∴C1（-2，3，3）， 
∵点P为线段DC1上一点（异于D，C1）， 
∴设DP→=λDC1→=（-2λ，3λ，3λ-3），A1B→=（0，3，-3）， 
设n→=（x，y，z）是平面A1PB的一个法向量， 
则{n→·AB→=3y-3z=0n→·A1P→=-2λx+3λy+(3λ-3)z=0，令z=2λ，则n→=（23λ-3，2λ，2λ）， 
∵DA，DA1，DB两两垂直，且DA∩DA1=D， 
∴DB⊥平面AA1D1D，∴平面AA1D1D的一个法向量为m→=（0，1，0）， 
设平面A1PB与平面AA1D1D夹角为θ， 
则cosθ=|n→·m→||n→|·|m→|=2λ20λ2-12λ+3=23λ2-12λ+20，0＜x＜1， 
∴当1λ=2时，即λ=12时，cosθ取得最大值， 
∴DP=12DC1=102时，面A1PB与面AA1D1D夹角的余弦值最大．

【解析】 
(1)连接BD，由几何关系证明AD⊥BD，再结合题意，证明AD⊥平面A1BD，由此能证明AD⊥A1B； 
(2)以D为坐标原点，建立空间直角坐标系，利用向量法求解． 
此题主要考查线线垂直、线面垂直的判定与性质、向量法求出二面角的余弦值的最大值等基础知识，考查运算求解能力，是中档题．

20.【答案】（1）解：令事件A=“甲平台日销售量不低于8件”， 
则P(A)=26+24+10100=35， 
令事件B=“从甲平台所有销售数据中随机抽取3天的日销售量，其中至少有2天日销售量不低于8件”， 
则P(B)=C32(35)225+C33(35)3=81125； 
（2）解：设甲平台的日销售收入为X， 
则X的所有可能取值为6a-240，7a-270，8a-300，9a-330，10a-360， 
所以，X的分布列为：
X
6a-240
7a-270
8a-300
9a-330
10a-360
P
14100
26100
26100
24100
10100
所以，E(X)=(6a-240)×14100+(7a-270)×26100+(8a-300)×26100+(9a-330)×24100+(10a-360)×10100=7.9a-297； 
设乙平台的日销售收入为Y， 
则Y的所有可能取值为6a-240，7a-280，8a-320，9a-355，10a-390， 
所以，Y的分布列为：
Y
6a-240
7a-280
8a-320
9a-355
10a-390
P
10100
25100
35100
20100
10100
所以，E(Y2)=(6a-240)×10100+(7a-280)×25100+(8a-320)×35100+(9a-355)×20100+(10a-390)×10100=7.95a-316； 
所以，E（Y）-E（X）=0.05a-19， 
令0.05a-19≥0得a≥380， 
令0.05a-19＜0得a＜380， 
所以，当300≤a＜380时，选择甲平台； 
当a=380时，甲乙平台均可； 
当380＜a≤500时，选择乙平台．
【解析】 
(1)根据古典概型求解即可得事件A的概率，再结合二项分布的概率公式求解即可得事件B的概率； 
(2)设甲平台的日销售收入为X，乙平台的日销售收入为Y，进而分别求其分布列，进而根据分布列求期望，比较期望大小即可得答案． 
此题主要考查了离散型随机变量的分布列和期望，属于中档题．

21.【答案】解：（1）∵双曲线C：x2a2-y2b2=1(a＞0，b＞0)的实轴长为2， 
∴a=1， 
∵点(7，-1)是抛物线E：x2=2py的准线与C的一个交点， 
∴7-1b2=1，解得b2=16， 
∴双曲线C的方程为x2-6y2=1， 
∵点(7，-1)是抛物线E：x2=2py的准线与C的一个交点， 
∴p2=1，∴p=2， 
∴抛物线E的方程为x2=4y． 
（2）由题意直线AB的斜率存在，∴设直线AB的方程为y=kx+m，A（x1，y1），B（x2，y2）， 
联立{y=kx+mx2=4y，得x2-4kx-4m=0， 
∴x1+x2=4k，x1x2=-4m， 
∵抛物线E的方程为x2=4y，∴y=14x2，y'=12x， 
∴切线AP：y-y1=12x1(x-x1)，结合y1=14x12，得y=12x1x-14x12， 
同理切线BP：y=12x2x-14x22， 
联立{y=12x1x-14x12y=12x2x-14x22，解得{x=x1+x22y=x1x24，即{x=2ky=-m，∴P（2k，-m）， 
又S△PAB=121+k2|x1-x2|•|2k2-(-m)+m|1+k2=(x1+x2)2-4x1x2|k2+m|=4|k2+m|32， 
且（2k）2-6（-m）2=1，即k2=6m2+14， 
∴S△PAB=4|k2+m|32=12|6m2+4m+1|32=12[6(m+12)2+13]32， 
又P（2k，-m）在双曲线上，∴m∈R， 
∴S△PAB=12[6(m+12)2+13]32≥12(13)32=318， 
∴△PAB面积的取值范围是[318，+∞）．
【解析】 
(1)代入点(7,-1)，结合双曲线C：x2a2-y2b2=1(a>0,b>0)的实轴长为2可得双曲线方程，根据抛物线的装配线方程可得抛物线方程； 
(2)设直线AB的方程为y=kx+m，A(x1,y1)，B(x2,y2)，根据几何意义求得切线AP，BP的方程，联立可得K的坐标，代入双曲线方程，结合面积表达式求解范围即可． 
此题主要考查双曲线、抛物线方程的求解，考查联立直线与圆锥曲线、利用韦达定理化简并表达面积的问题及利用导数求切线方程等基础知识，考查运算求解能力，是中档题．

22.【答案】解：（1）g（x）=f′（x）=2ae2x-2x， 
所以g′（x）=4ae2x-2， 
当a≤0时，g′（x）＜0，g（x）在（-∞，+∞）上单调递减， 
当x→-∞时，g（x）→-∞时，g（x）→+∞， 
当x→+∞时，g（x）→-∞， 
由零点的存在定理，此时g（x）存在唯一零点， 
当a＞0时，令g′（x）=4ae2x-2＞0，得x＞-ln2a2， 
故当x∈（-ln2a2，+∞），g′（x）＞0，g（x）单调递增， 
同理，x∈（-∞，-ln2a2）时，g（x）单调递减， 
所以g（x）min=g（-ln2a2）=1+ln2a， 
当x→-∞时，g（x）→+∞， 
当x→+∞时，g（x）→+∞， 
所以当g（-ln2a2）＜0，即0＜a＜12e， 
由零点的存在定理g（x）存在两个零点， 
当a＞12e时，g（x）在（-∞，+∞）无零点， 
综上所述，当a≤0或a=12e时，g（x）存在1个零点， 
当0＜a＜12e时，g（x）存在2个零点， 
当a＞12e时，f（x）无零点． 
（2）由（1）知，f（x）的极值点为x1，x2，即方程g（x）=2ae2x-2x=0的两个根， 
且0＜a＜12e， 
所以ae2x1=x1＞0，ae2x2=x2＞0， 
两式相除并取对数得2（x2-x1）=lnx2x1＞0， 
由ee-1x1+x2≥λx1x2，得2（x2-x1）（ee-2x1+x2）≥λx1x2•lnx2x1， 
所以λ≤2(2e-2+x2x1-ee-2·x1x2)lnx2x1， 
令t=x2x1＞1，令h（t）=2(2e-2+t-ee-21t)lnt（t＞1）， 
则λ≤h（t）恒成立， 
h′（t）=2(t2+ee-2lnt)-(ee-2t+t2-ee-2)t2ln2t， 
令φ（t）=（t2+ee-2）lnt-（2e-2t+t2-ee-2）， 
则φ′（t）=2tlnt-t+ee-2•1t-2e-2， 
因为φ″（t）=2lnt+1-ee-2•1t2在（1，+∞）上单调递增，且φ″（1）＜0，φ″（e）＞0， 
所以∃t0∈（1，e），使得φ″（t0）=0，且当t∈（1，t0）时，φ″（t）＜0，φ′（t）单调递减， 
当t∈（t0，+∞）时，φ″（t）＞0，φ′（t）单调递增， 
又φ′（1）=0，φ′（e）＞0， 
由零点的存在定理，存在t1∈（1，e）， 
当t∈（1，t1）时，φ′（t）＜0，φ（t）单调递减， 
当t∈（t1，+∞）时，φ′（t）＞0，φ（t）单调递增， 
又φ（1）=φ（e）=0， 
所以x∈（1，e）时，φ（t）＜0，h（t）单调递减， 
当x∈（e，+∞）时，φ（t）＞0，h（t）单调递增， 
所以当t=e时，h（t）min=h（e）=2(e-1)2e-2， 
所以λ的取值范围为λ≤2(e-1)2e-2， 
所以λ的取值范围为（-∞，2(e-1)2e-2]．
【解析】 
(1)根据题意可得g(x)=f'(x)=2ae2x-2x，求导得g'(x)=4ae2x-2，分三种情况：当a⩽0或a=12e时，当012e时，讨论函数f(x)零点的个数． 
(2)由(1)知，f(x)的极值点为x1，x2，即ae2x1=x1>0，ae2x2=x2>0，两式相除并取对数得2(x2-x1)=lnx2x1>0，不等式可化为2(x2-x1)(ee-2x1+x2)⩾λx1x2，λ⩽2(2e-2+x2x1-ee-2·x1x2)lnx2x1，只需λ⩽[2(2e-2+x2x1-ee-2·x1x2)lnx2x1]min，即可得出答案． 
此题主要考查导数的综合应用，解题中注意注意分类讨论思想，转化思想的应用，属于难题．