中考数学专题复习全攻略：第三节 与圆有关的计算 含解析答案

第三节  与圆有关的计算

知识点一 ：正多边形与圆

正多边形与圆

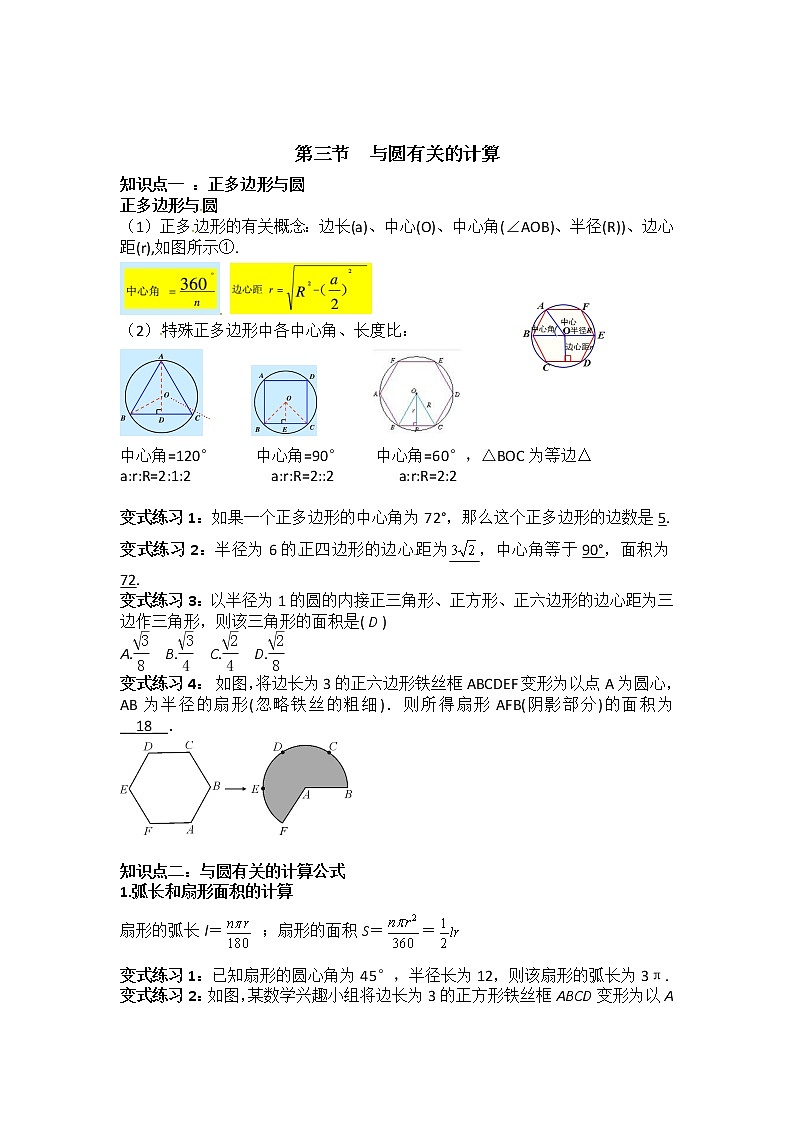
（1）正多边形的有关概念：边长(a)、中心(O)、中心角(∠AOB)、半径(R))、边心距(r),如图所示①.

（2）特殊正多边形中各中心角、长度比：

中心角=120°     中心角=90°    中心角=60°，△BOC为等边△

a:r:R=2:1:2          a:r:R=2::2        a:r:R=2:2

变式练习1：如果一个正多边形的中心角为72°，那么这个正多边形的边数是5.

变式练习2：半径为6的正四边形的边心距为，中心角等于90°，面积为72.

变式练习3：以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是( D )

A.  B.  C.  D.

变式练习4： 如图，将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心，AB为半径的扇形(忽略铁丝的粗细)．则所得扇形AFB(阴影部分)的面积为__18__．

知识点二：与圆有关的计算公式 

1.弧长和扇形面积的计算 

扇形的弧长l＝ ；扇形的面积S＝＝[来源

变式练习1：已知扇形的圆心角为45°，半径长为12，则该扇形的弧长为3π.

变式练习2：如图，某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形(忽略铁丝的粗细)，则所得扇形DAB的面积为(　　)

第2题图

A. 6            B. 7          C. 8              D. 9

【解析】D根据扇形的面积公式进行计算，由题意可知l＝3＋3＝6，∴S扇形DAB＝lr＝×6×3＝9.

2.圆锥与侧面展开图

（1）圆锥侧面展开图是一个扇形，扇形的半径等于圆锥的母线，扇形的弧长等于圆锥的底面周长.

（2）计算公式：

,S侧==πrl

变式练习1：如图，把一个圆锥沿母线OA剪开，展开后得到扇形AOC，已知圆锥的高h为12 cm，OA＝13 cm，则扇形AOC中的长是________ cm(计算结果保留π)．

第1题图

【解析】10π由勾股定理得圆锥底面圆的半径r＝＝＝5 cm，则圆锥侧面展开扇形的弧长等于圆锥底面圆的周长：l＝2πr＝10π cm.

变式练习2：如图，三个小正方形的边长都为1，则图中阴影部分面积的和是________(结果保留π)．

第2题图

【解析】π如解图，∵在Rt△BDC中，∠DBC＋∠BDC＝90°，∠ABE＝45°，∴三个圆心角之和为∠ABE＋∠DBC＋∠BDC＝45°＋90°＝135°.三个扇形的半径为1，利用扇形面积公式S＝得：S阴影＝＝π.

第2题解图

变式练习3：如图，在ABCD中，AD＝2，AB＝4，

∠A＝30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是________(结果保留π)．

第3题图

【解析】3－　如解图，过点D作DF⊥AB，垂足为F, ∵AD＝2，∠A＝30°， ∴DF＝AD＝1，又∵AB＝4，AE＝AD＝2，∴BE＝2，∴S阴影＝S▱ABCD－S扇形ADE－S△BCE＝4×1－－×2×1＝3－.

第3题解图

变式练习4：如图，扇形AOB中，OA＝2，C为上的一点，连接AC，BC，如果四边形AOBC为菱形，则图中阴影部分的面积为(　　)

A. －                           B. －2

C. －                                    D. －2

　【解析】D如解图，连接OC，过点A作AD⊥OC于点D，∵四边形AOBC是菱形，∴OA＝AC＝2.∵OA＝OC，∴△AOC是等边三角形，∴∠AOC＝∠BOC＝60°，∴△ACO与△BOC为边长相等的两个等边三角形．∵AO＝2，∴AD＝OA·sin60°＝2×＝，∴

S阴影＝S扇形AOB－2S △AOC＝－2××2×＝－2.

变式练习5：如图，圆锥底面半径为r cm，母线长为10 cm，其侧面展开图是圆心角为216°的扇形，则r的值为( B )

A．3  B．6  C．3π  D．6π