湘教版八年级下册2.2.2平行四边形的判定说课课件ppt

这是一份湘教版八年级下册2.2.2平行四边形的判定说课课件ppt，共15页。PPT课件主要包含了几何语言，知识回顾，定义法，新知探究，疑问升级，∴∠3∠4，∴AD∥BC，又AB∥DC，∴BEFD，又∵BE∥FD等内容，欢迎下载使用。

平行四边形的对边平行；对边相等
平行四边形的对角相等；邻角互补
平行四边形的对角线互相平分
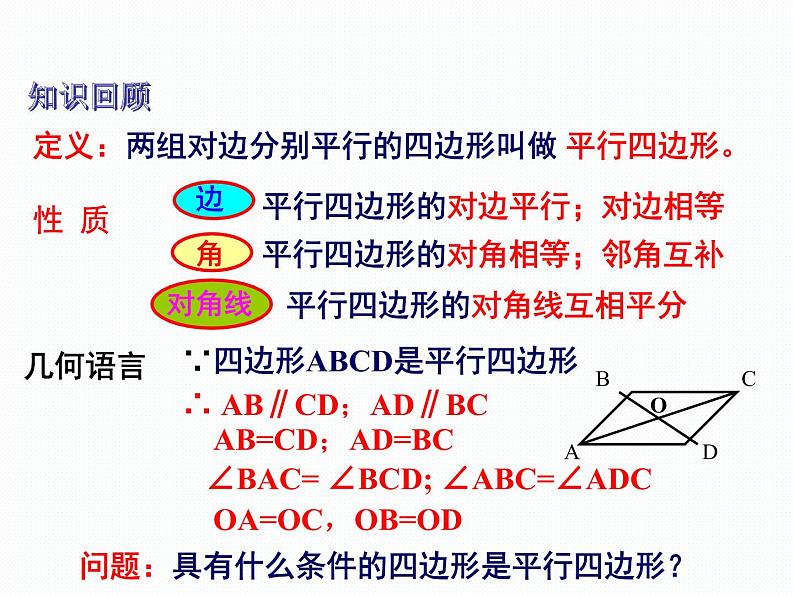
定义：两组对边分别平行的四边形叫做 平行四边形。
∵四边形ABCD是平行四边形∴ AB∥CD；AD∥BC AB=CD；AD=BC ∠BAC= ∠BCD; ∠ABC=∠ADC OA=OC，OB=OD
问题：具有什么条件的四边形是平行四边形？
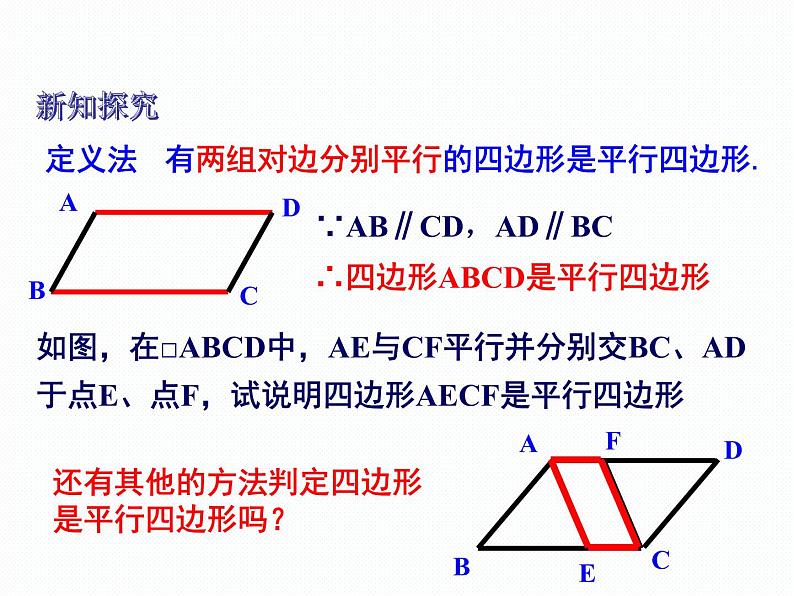
有两组对边分别平行的四边形是平行四边形.
∵AB∥CD，AD∥BC
∴四边形ABCD是平行四边形
如图，在□ABCD中，AE与CF平行并分别交BC、AD于点E、点F，试说明四边形AECF是平行四边形
还有其他的方法判定四边形是平行四边形吗？
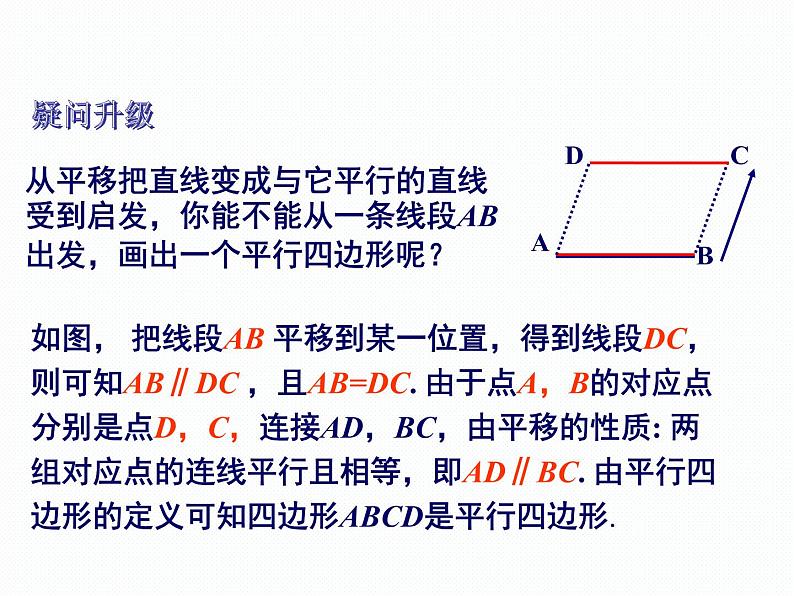
从平移把直线变成与它平行的直线受到启发，你能不能从一条线段AB 出发，画出一个平行四边形呢？
如图， 把线段AB 平移到某一位置，得到线段DC， 则可知AB∥DC ，且AB=DC. 由于点A，B的对应点分别是点D，C，连接AD，BC，由平移的性质: 两组对应点的连线平行且相等，即AD∥BC. 由平行四边形的定义可知四边形ABCD是平行四边形.
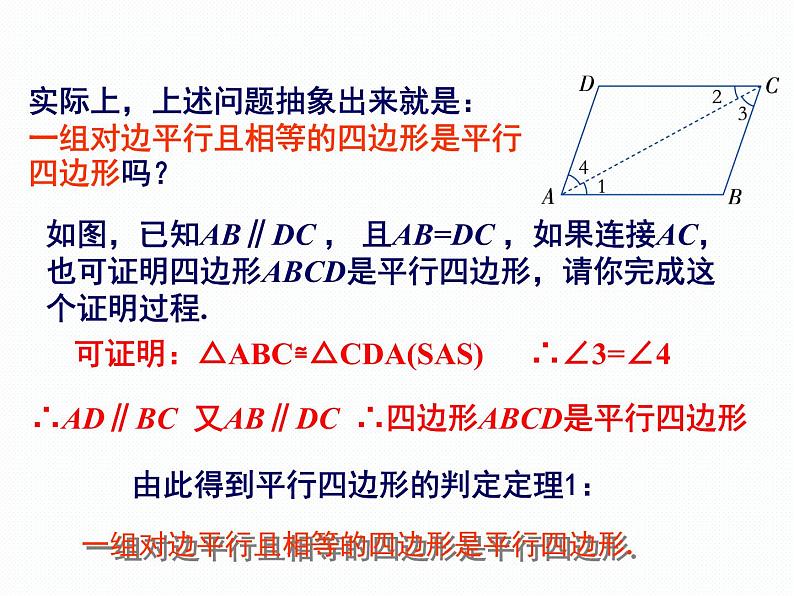
实际上，上述问题抽象出来就是：一组对边平行且相等的四边形是平行四边形吗？
如图，已知AB∥DC ， 且AB=DC ，如果连接AC，也可证明四边形ABCD是平行四边形，请你完成这个证明过程.
可证明：△ABC≌△CDA(SAS)
由此得到平行四边形的判定定理1：
一组对边平行且相等的四边形是平行四边形.
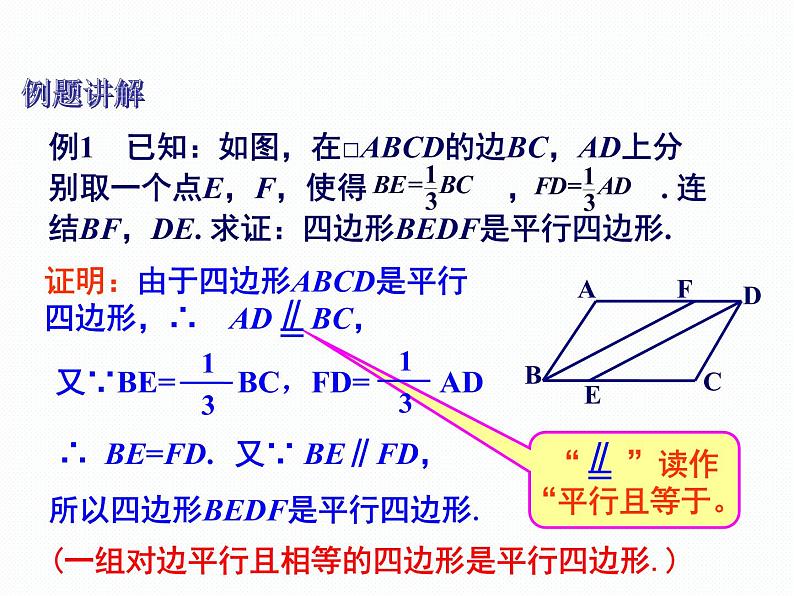
所以四边形BEDF是平行四边形.(一组对边平行且相等的四边形是平行四边形.)
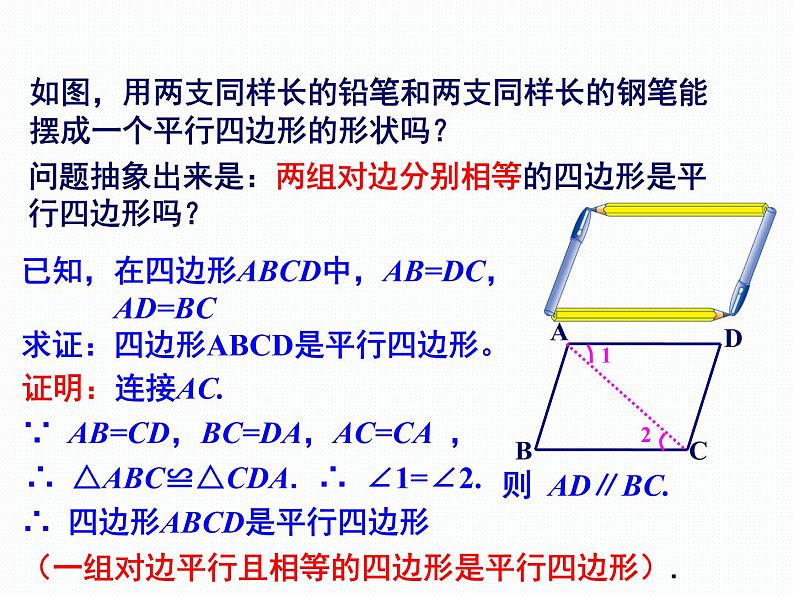
如图，用两支同样长的铅笔和两支同样长的钢笔能摆成一个平行四边形的形状吗？
问题抽象出来是：两组对边分别相等的四边形是平行四边形吗？
已知，在四边形ABCD中，AB=DC， AD=BC求证：四边形ABCD是平行四边形。
∵ AB=CD，BC=DA，AC=CA ，
∴ △ABC≌△CDA.
∴ 四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）.
由此得到平行四边形的判定定理2：
两组对边分别相等的四边形是平行四边形.
例2、如图，在四边形ABCD中，△ABC≌△CDA.求证：四边形ABCD是平行四边形.
∴ 四边形ABCD是平行四边形.
∴ AB=DC ，AD=BC .
证明： ∵ △ABC≌△CDA ，
例3.如图，四边形ABCD中，CF⊥BC交BD于点F，AD∥BC，AE⊥AD交BD于点E， 且AE=CF.求证:(1)四边形ABCD是平行四边形． (2) AF=EC.
证明：(1) ∵ AD∥BC，
(2) ∵△ AED≌△CFB， ∴∠AED=∠CFB ∴ AE ∥ FC ， ∵ AE=FC, ∴四边形AECF是平行四边形．∴ AF=EC.
∴AD=BC，∵AD∥BC，∴四边形ABCD是平行四边形．
∴△AED≌△CFB(AAS)
∴∠ADE=∠CBF
又CF⊥BC ，AE⊥AD
∴∠EAD=∠FCB=90°，AE=CF
1.如图，是由12个边长相等的正三角形镶嵌而成的平面图形，则图中的平行四边形共有 个.
两个正三角形所组成的平行四边形有6+6+1=13个；
四个正三角形所组成的平行四边形有6个，
六个正三角形所组成的平行四边形有2个；
3.四边形的三个内角的度数依次如下选项，其中是平行四边形的是（ ） 88°108°88° B. 88°104°108° C. 88°92°92° D. 88°92°88°
4.已知：四边形ABCD中，AD∥BC，分别添上下列条件：①AB∥CD；②AB=CD；③AD=BC；④∠A=∠C；⑤∠B=∠C；⑥∠A+∠D=∠B+∠C.能使四边形ABCD为平行四边形的有( )A.①②③④ B.①③④⑤C.①④⑤⑥ D.①③④⑥
5.如图，在□ABCD中，AE= CF. 求证：四边形EBFD是平行四边形.
6.如图，在四边形ABCD中，AB=DC，BC=AD，E，F 分别是边BC，AD的中点. 找出图中所有的平行四边形，并且说出理由.
解：□ABCD：两组对边分别相等的 四边形是平行四边形. □ABEF 和□ FECD ：一组对边 平行且相等的四边形是平行四边形.
7.如图，E，F是四边形ABCD的对角线AC上两点，AF=CE，DF=BE，DF∥BE. 求证：（1）△AFD≌ △ CEB； （2）四边形ABCD是平行四边形.
8.已知： □ABCD中，E，F分别是边AD，BC的中点.求证：四边形EBFD是平行四边形.
如果把结论换成“求证：BE=FD”，你会证吗？
（1）由DF∥BE. 得：∠DFE=∠BEF ， ∴∠AFD=∠BEC 又AF=CE，DF=BE，结论得证。
（2）可证得：AD=BC，AB=DC
9.如图， □ABCD中，∠ABC=60°，E、F分别在CD、BC的延长线上，AE∥BD，EF⊥BC，DF=2，求EF的长。
10.如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD和等边△ABE.已知∠BAC=30°，EF⊥AB，垂足为F，连结DF. （1）试说明AC=EF；（2）求证：四边形ADFE是平行四边形.
可证得四边形ABDE是平行四边形，
△CEF是直角三角形。
∠ECF=∠ABC=60°
（1）可证△ACB≌△EFA(AAS)，
（2）由(1)得：AD＝EF，∠DAF=60°＋30°=90°=∠EFA.∴AD∥EF