中职数学高教版（中职）基础模块下册(2021)6.2.2 直线的点斜式方程与斜截式方程评优课教学ppt课件

这是一份中职数学高教版（中职）基础模块下册(2021)6.2.2 直线的点斜式方程与斜截式方程评优课教学ppt课件，共18页。PPT课件主要包含了学习目标，即yy0，即yx+5，化简得ykx+b，对截距的理解，一次函数，k直线的斜率，0-1，0-3，化简得y2x+3等内容，欢迎下载使用。

第六章 直线与圆的方程 6.2.2 直线的点斜式方程和斜截式方程
在初中，我们用过“自然数集”“有理数集”等表述，这里的“集”就是集合的简称，那么什么是集合呢？
探究一. 直线的点斜式方程
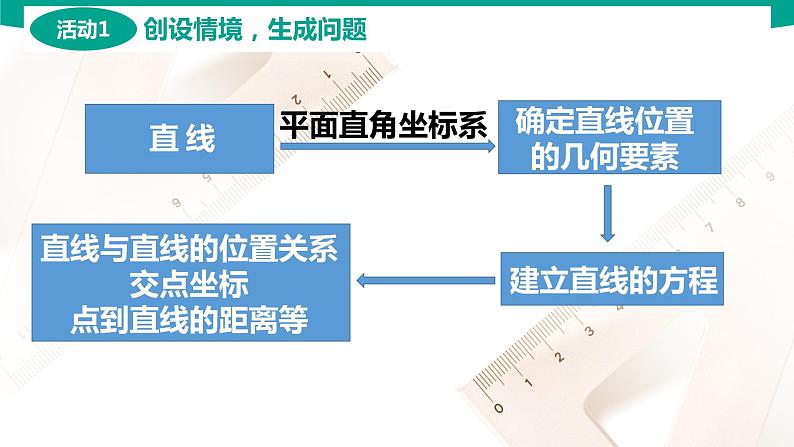
回顾：确定一条直线的两个要素：
直线上一点和直线的方向，
所以，已知直线上一点和这条直线的斜率，可以唯一确定这条直线.
如何建立直线的方程？回顾直线方程的定义
问题1：求过点P0(x0 , y0 )，且斜率是k的直线的方程.
若直线上每一个点的坐标都符合某个方程，则这个方程就是这条直线的方程.
因此，我们设直线?上不同于P0的任意一点的坐标为P(x,y)
一条直线的斜率可以用这条直线上的两个不同点的坐标来表示.
整理得：y-y0=k(x-x0)
直线 ?上任一点的坐标(x,y)都符合该方程，所以该方程是直线 ?的方程.
直线 ?的方程是由直线上一点及直线的斜率确定的，因此，这个方程称为直线的点斜式方程.
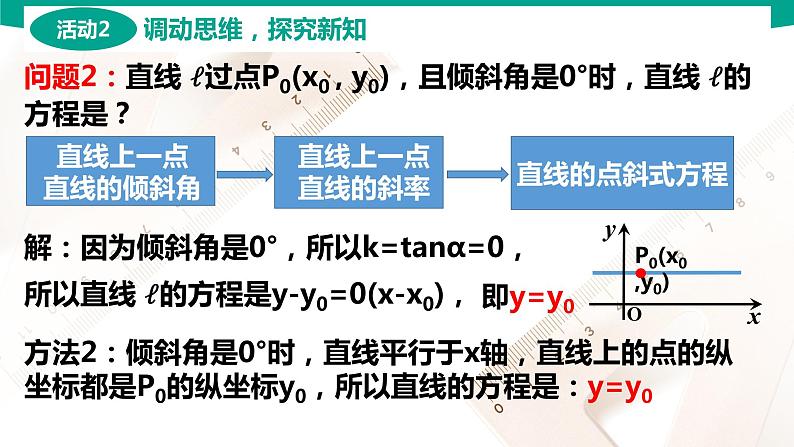
问题2：直线 ?过点P0(x0 , y0)，且倾斜角是0°时，直线 ?的方程是？
解：因为倾斜角是0°，所以k=tanα=0，
所以直线 ?的方程是y-y0=0(x-x0)，
方法2：倾斜角是0°时，直线平行于x轴，直线上的点的纵坐标都是P0的纵坐标y0，所以直线的方程是：y=y0
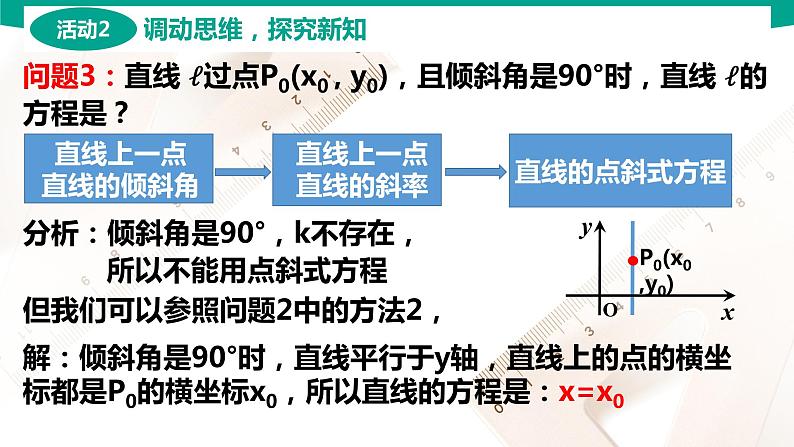
问题3：直线 ?过点P0(x0 , y0)，且倾斜角是90°时，直线 ?的方程是？
分析：倾斜角是90°，k不存在， 所以不能用点斜式方程
但我们可以参照问题2中的方法2，
解：倾斜角是90°时，直线平行于y轴，直线上的点的横坐标都是P0的横坐标x0，所以直线的方程是：x=x0
点斜式方程使用条件：斜率存在
例1. 已知直线过点P0(-2 , 3)，倾斜角α=45°，求直线的方程.
解：∵ α=45°，∴ k=tanα=tan45°=1
根据点斜式方程可得y-3=1×[x-(-2)]
探究二. 直线的斜截式方程
根据点斜式方程可得：y-b=k(x-0)
该式称为直线的斜截式方程
如何表示过点P0(0 , b)，斜率为k的直线方程？
截距不是距离，截距是直线与坐标轴的交点坐标.
所以截距可正，可负，也可以是0，
y轴上的截距代表直线与y轴交点的纵坐标,令x=0,求出y的值.
如:直线y=2x-4在x轴上的截距是___,在y轴上的截距是___.
x轴上的截距代表直线与x轴交点的横坐标,令y=0,求出x的值.
直线的斜截式方程是特殊的点斜式方程，两者都只能表示斜率存在的直线.
问：直线的斜截式方程y=kx+b，它的表达式你能想到什么？
问：如何从直线方程的角度认识一次函数y=kx+b?
b：直线在y轴上的截距
例2. 一次函数y=2x-1，y=-x-3，y=3x 对应的图像都是直线，请填写下表：
例3. 已知直线的在y轴上的截距为2，倾斜角是60°，求直线的方程.
思考：已知直线上的两点，如何求直线的方程？
例4. 已知直线过点A(1,5)，B(-2,-1)，求直线的方程
分析：已知直线上的两点可以求得直线的斜率，再结合其中一点即可由点斜式得到直线的方程.
所以，直线的方程为：y-5=2(x-1)，
总结：已知两点，先求斜率，再利用点斜式写出方程
(1). 直线的点斜式方程：
(2). 直线的斜截式方程：
y-y0=k(x-x0) (适用于斜率存在的直线)
y=kx+b(适用于斜率存在的直线)
(3). 截距的理解：
直线在x轴上的截距是与x轴交点的横坐标，
直线在y轴上的截距是与y轴交点的横坐标.
(4). 斜截式与一次函数的联系：
一次函数y=kx+b，其中k代表直线的斜率，b代表直线在y轴上的截距.