四川省绵阳市2022-2023学年九年级上学期期末数学试题

2022～2023学年上期末综合素质测评

九年级数学试卷
第Ⅰ卷（选择题，共36分）

一、选择题：本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（    ）．

A．B．C．D．

2．若1是关于x的一元二次方程的一个根，则a的值为（    ）．

A．    B．0    C．1    D．0或1

3．三根电线，其中只有两根电线通电，接上小灯泡能正常发光．小明从三根电线中，随意选择两根电线，接上小灯泡的正负极，能发光的概率是（    ）．

A．    B．    C．    D．

4．一根钢管放在V形架内，其横截面如图所示，钢管的半径是15cm，如果，则（    ）．

A．18cm    B．20cm    C．25cm    D．30cm

5．一次函数和反比例函数的一个交点坐标为，则另一个交点坐标为（    ）．

A．   B．   C．   D．

6．如图，为的内切圆，切点分别为M，N，Q，已知，，，则的半径为（    ）．

A．    B．    C．1    D．2

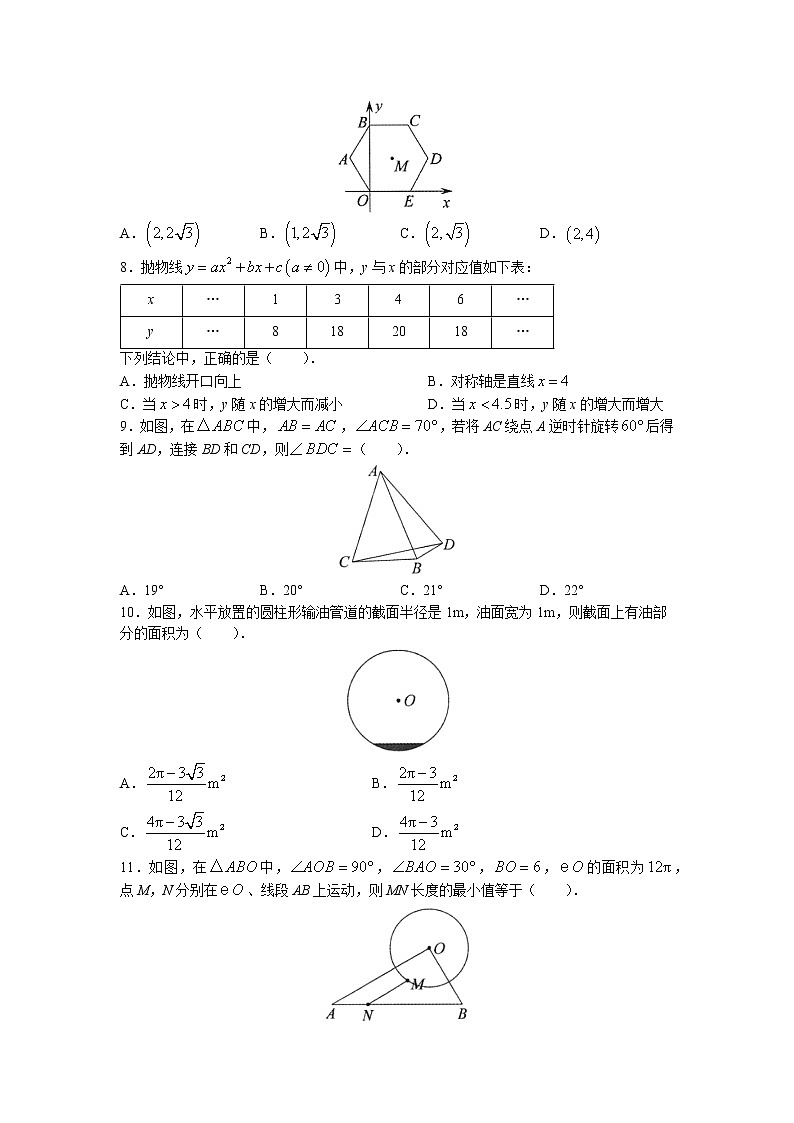
7．如图，在平面直角坐标系中，正六边形OABCDE的边长是4，则它的内切圆圆心M的坐标是（    ）．

A．   B．   C．   D．

8．抛物线中，y与x的部分对应值如下表：

下列结论中，正确的是（    ）．

A．抛物线开口向上       B．对称轴是直线

C．当时，y随x的增大而减小    D．当时，y随x的增大而增大

9．如图，在中，，，若将AC绕点A逆时针旋转后得到AD，连接BD和CD，则∠（    ）．

A．19°    B．20°    C．21°    D．22°

10．如图，水平放置的圆柱形输油管道的截面半径是1m，油面宽为1m，则截面上有油部分的面积为（    ）．

A．      B．

C．      D．

11．如图，在中，，，，的面积为，点M，N分别在、线段AB上运动，则MN长度的最小值等于（    ）．

A．    B．    C．    D．

12．如图，在平面直角坐标系中，O为坐标原点，点A为x轴上的一点，将OA绕点O按顺时针旋转60°至OB，反比例函数的图象经过点B，过A作交反比例函数图象于点C，若的面积为，则k的值为（    ）．

A．   B．   C．   D．

第Ⅰ卷（非选择题，共114分）

二、填空题：本大题共6个小题，每小题4分，共24分．把答案填写在答题卡的横线上．

13．如图，在中，已知，则______．

14．已知点与点关于原点对称，则______．

15．将二次函数的图象向右平移1个单位，再向下平移一个单位，得到对应函数图象的解析式为______．

16．一个质地均匀的小正方体，六个面分别标有数字“1”，“2”，“3”，“4”，“5”，“6”，连续抛掷两次该正方体，得到第一次朝上一面的数字是第二次朝上一面的数字的两倍的概率是______．

17．春季流感病毒传播速度快，我们要做好预防。如果有一个人患了流感，经过两轮传染后共有256人患了流感，则每轮传染中平均一个人传染了______人．

18．已知的弦，优弧上的点到AB的最大距离为1.6，直线，若上有4个不同的点到l的距离等于0.4，则点O到l的距离d的范围为______．

三、解答题：本大题共7个小题，共90分．解答应写出文字说明、证明过程或演算步骤．

19．（本题满分16分，每小题8分）

（1）解方程：．

（2）如图，的三个顶点坐标分别为，，．

①画出将绕点A顺时针旋转90°得到的，并写出点D，E的坐标；

②请在图中作出的外接圆，写出圆心M的坐标．

20．（本题满分12分）

已知关于x的一元二次方程有两个不相等的实数根．

（1）求实数k的取值范围；

（2）若原方程的两个实数根为，，是否存在实数k，使得成立，若存在，求k的值；若不存在，请说明理由．

21．（本题满分12分）

一个不透明的箱子中装有1张白色的卡片和若干张红色的卡片，这些卡片除颜色外，大小、形状、厚度等均相同．某学习小组做试验：将卡片搅匀后从中任意摸出1张卡片，记下颜色后放回；搅匀后再摸一张卡片，记下颜色后放回；不断重复上述过程，获得数据如下：

（1）根据上表估计，任意摸一次为白色卡片的概率为0.25（精确到0.01），求红色卡片有多少张？

（2）现从该箱子中先后各摸出1张卡片，求恰好两张卡片颜色相同的概率．

22．（本题满分12分）

如图，一次函数与反比例函数在第一象限交于A，B两点，AC垂直x轴于点C，O为坐标原点，．

（1）求反比例函数的解析式；

（2）求点B的坐标，并直接写出的解集；

（3）点D在y轴上，满足的面积和的面积相等，求点D的坐标．

23．（本题满分12分）

目前，随着新冠病毒毒力减弱，国家对新冠疫情防控的政策更加科学化，人们对新冠病毒的认识更加理性、佩戴口罩可以阻断传播途径，在一定程度上能够有效防止感染新型冠状病毒肺炎．某药品销售店将购进一批A、B两种类型口罩进行销售，A型口罩进价m元每盒，B型口罩进价30元每盒，若各购进m盒，成本为1375元．

（1）求A型口罩的进价为多少元？

（2）设两种口罩的售价均为x元．当A型口罩售价为30元时，可销售60盒，售价每提高1元，少销售5盒；B型口罩的销量y（盒）与售价x之间的关系为；若B型口罩的销售量不低于A型口罩的销售量的10倍，该药品销售店如何定价？才能使两种口罩的利润总和最高．

24．（本题满分12分）

如图，的顶点A，D在上，边BC切于点M，连接AM，DM，CD交于点N．

（1）如图1，求证：；

（2）如图2，若圆心O在边AD上，连接AN，MN，若，，，求的半径．

25．（本题满分14分）

如图，抛物线的图象与x轴交于A，B两点，，对称轴是直线，与y轴交于点．

（1）求抛物线的解析式；

（2）如图，矩形DEFG的边DE在x轴上，顶点F，G在x轴上方的抛物线上，设点D的横坐标为d，当矩形DEFG的周长取最大值时，求d，并求矩形DEFG的周长的最大值；

（3）在（2）的结论下，直线DG上是否存在点M，使得，若存在，求出M的坐标；若不存在，请说明理由．

2022～2023学年上期末综合素质测评

九年级数学参考答案

一、选择题：本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．B 2．C 3．B 4．D 5．A 6．C 7．A 8．D 9．B 10．A

11．C 12．D

二、填空题：本大题共6小题，每小题4分，共24分．将答案直接填写在题中横线上．

13．40° 14．0  15．  16．  17．15  18．

三、解答题：本大题共6小题，共46分，解答应写出文字说明、证明过程或演算步骤．

19．解：（1）移项，得．

∵，，，

∴，

∴．

∴原方程的解为，．

（2）①所作如图所示，

点D，E的坐标分别为，．

②所作如图所示，M的坐标．

20．解：（1）∵方程有两个不相等的实数根，

∴，解得．

又二次项系数不为0，即，

∴实数k的取值范围为且．

（2）∵原方程的两个实数根为，，

∴由根与系数的关系得．

又，∴，解得．

21．解：（1）∵摸到白色卡片的概率为0.25，有1张白色卡片，

∴摸到红色卡片的概率为0.75．

设卡片总张数为n．

∴，解得．

∴红色卡片的总数为（张）．

（2）记白色卡片为W，三张红色卡片分别为，，．

从该箱子中先后各摸出1张卡片，可能的情况有，，，，，，，，，，，．

共有种结果，其中摸到两张卡片颜色相同的结果有种．

∴两张卡片颜色相同的概率为．

22．解：（1）设，则．

∴，．

∵直线AB解析式为，∴，解得，∴．

∴，∴反比例函数的解析式为．

（2）由，解得或，∴．

∴由图知的解集为或．

（3）由（1）（2）得，，．

∵直线AB的解析式．

令，得，

∴直线AB与x轴的交点的横坐标为5，与y轴的交点E的纵坐标为5．

∵的面积和的面积相等，

∴．

又点C的横坐标为1，

∴将直线AB向左平移4个单位，得到直线CD，

∴直线CD的解析式为．

令，则，∴点D的坐标为．

∵点关于点的对称点为，

由题意得点也满足的面积和的面积相等，

∴点D的坐标为或．

23．解：（1）由题意，得，

即，整理得，

∴，解得，（舍）．

答：A型口罩的进价为25元，B型口罩的进价为30元．

（2）由题意，得，解得．

设两种口罩的利润总和为w元．

由题意，得．

∴对称轴为，

∵，∴当时，w随x的增大而减小．

∵，

∴当时，两种口罩的利润总和最高，即定价为40元时，利润最高．

24．解：（1）证明：如图，连接MO并延长交AD于点I．

∵BC切于点M，∴．

∵，∴，

∴，∴．

又MI过圆心，∴MI垂直平分AD，∴．

（2）设，．

则，∴．

∵AD是直径，∴．

由（1）得，∴，

∴．

作于点H，

∴．

在中，，

∴，∴．

在中，．

在中，，

∴．

∵，∴，∴．

在中，，

解得，（舍去）．

∴，∴的半径为．

25．解：（1）设抛物线的解析式为．

由题意，得，解得．

∴该抛物线的解析式为．

（2）由抛物线的对称轴为．

∵，则，，

∴，，

∴矩形DEFG的周长

．

∴当，矩形DEFG的周长的最大值为．

（3）存在．设．

由（2）得，，，

当时，，
∴．

设，则，

∵矩形DEFG．

∴，

，，

∴，，

∴，

∴，∴．

∵，当点M在DE的上方时，，则．

在中，，解得．

当，，舍去．

∴．

当点M在DE的下方时，在FE的延长线上取点H，使得，

过M作，连接ME．

∵，，

∴，

∴，∴．

设，则，

于是，，，

在中，由勾股定理，得，

，

解得，舍去负值，．

．

综上所述，直线DG上存在点或，使得．