2023届高考数学二轮复习专题05三角恒等变换学案含解析

这是一份2023届高考数学二轮复习专题05三角恒等变换学案含解析，共48页。学案主要包含了核心先导，考点再现，解法解密，考点解密，分层训练等内容，欢迎下载使用。
 专题05 三角恒等变换
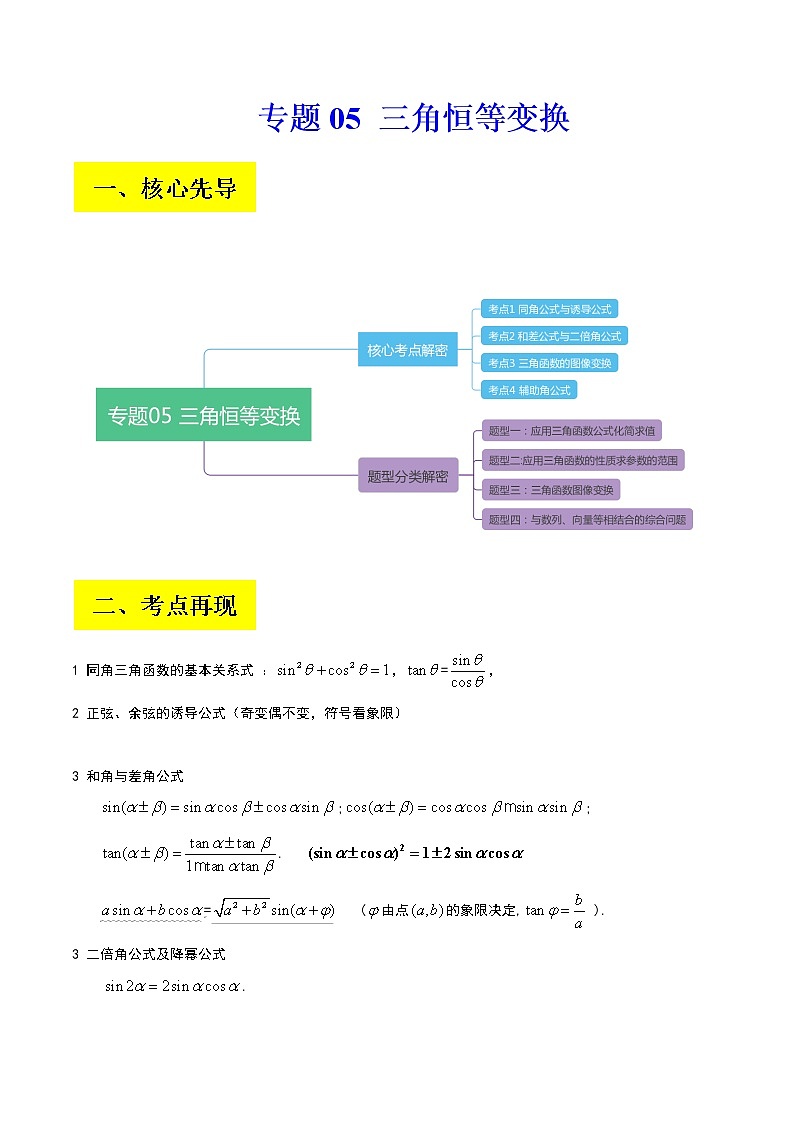
一、核心先导



二、考点再现

1 同角三角函数的基本关系式 ：，=，
2 正弦、余弦的诱导公式（奇变偶不变，符号看象限）

3 和角与差角公式
;;
.
= (由点的象限决定, ).
3 二倍角公式及降幂公式
.

.

4 三角函数的周期公式
函数， (A,ω,为常数，且A≠0)的周期；
函数，(A,ω,为常数，且A≠0)的周期.
三角函数的图像：

三、解法解密

1．基本公式的变形
(1)、 诱导公式的记忆口诀：奇变偶不变,符号看象限．[来源:学科网ZXXK]
(2)、同角三角函数基本关系式的常用变形：
(sin α±cosα)2＝1±2sin αcosα；(sin α＋cosα)2＋(sin α－cosα)2＝2；
(3)、降幂公式：cos2α＝,sin2α＝.
(4)、升幂公式：1＋cos 2α＝2cos2α,1－cos 2α＝2sin2α.
(5)、辅助角公式：asinx＋bcosx＝sin(x＋φ),其中sin φ＝,cosφ＝.
2．对称与周期
(1)、正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是个周期．
(2)、正切曲线相邻两对称中心之间的距离是半个周期．
3．奇偶性
若f(x)＝Asin(ωx＋φ)(A,ω≠0),则(1)f(x)为偶函数的充要条件是φ＝＋kπ(k∈Z)；(2)f(x)为奇函数的充要条件是φ＝kπ(k∈Z)．
4．由y＝sin ωx到y＝sin(ωx＋φ)(ω>0,φ>0)的变换：向左平移个单位长度而非φ个单位长度．
5．函数y＝Asin(ωx＋φ)的对称轴由ωx＋φ＝kπ＋,k∈Z确定；对称中心由ωx＋φ＝kπ,k∈Z确定其横坐标．
6.三角形中的三角函数关系
(1)、sin(A＋B)＝sin C；(2)、cos(A＋B)＝－cos C；(3)、sin ＝cos ；(4)、cos ＝sin .
7.若G是△ABC的重心，则＋＋＝0.
8.在△ABC中，若·