







湘教版八年级下册2.3 中心对称和中心对称图形公开课ppt课件
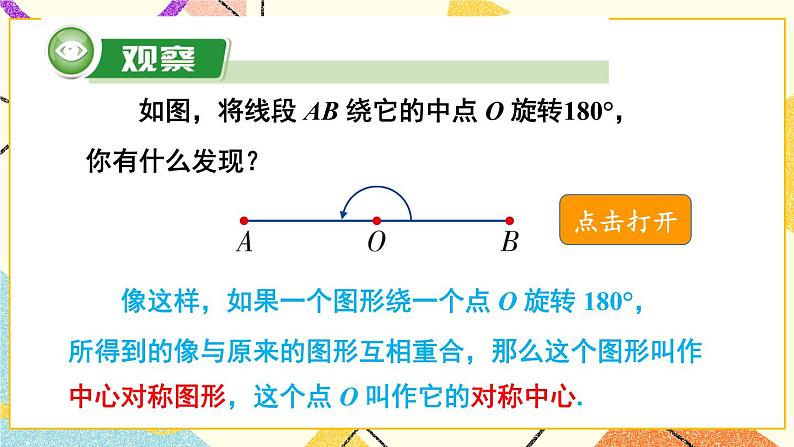
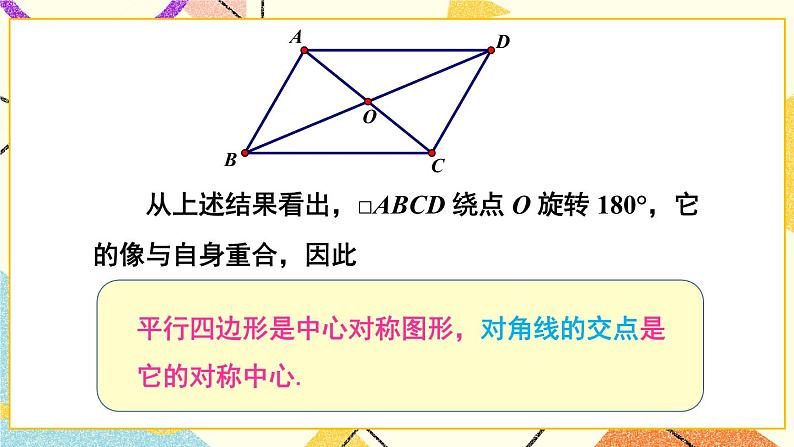
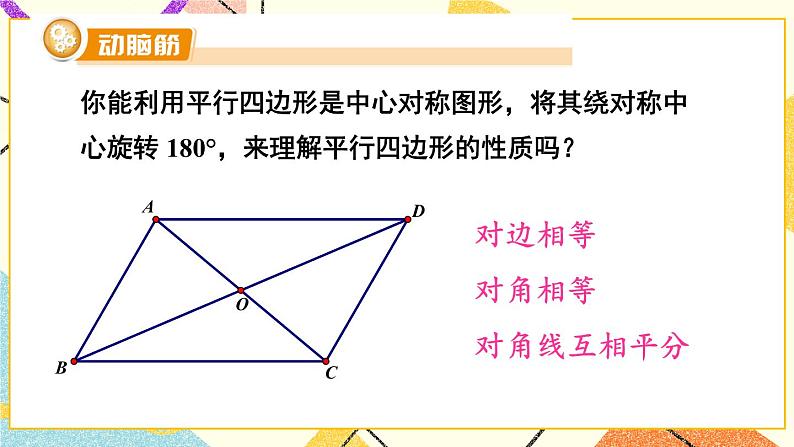
展开(1)把一个图案绕点 O 旋转 180°,你有什么发现?
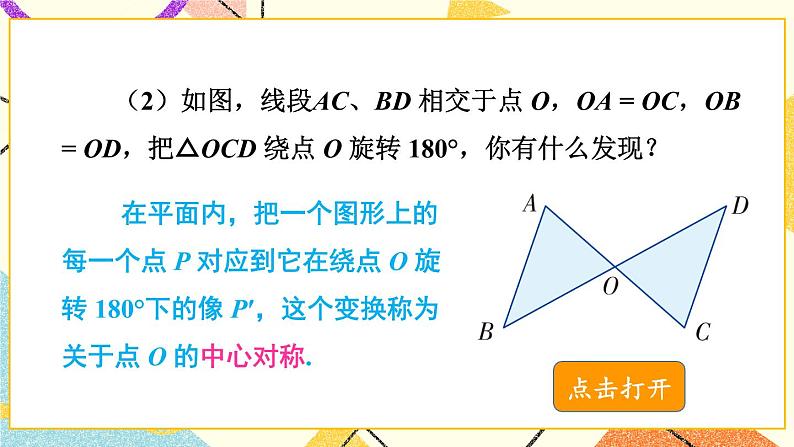
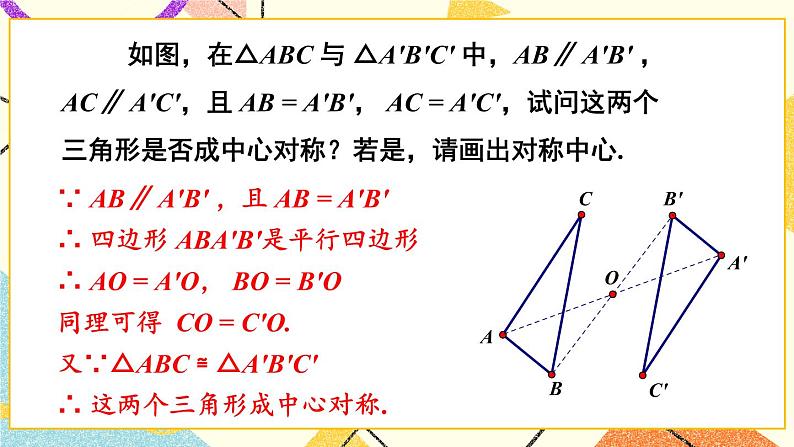
(2)如图,线段AC、BD 相交于点 O,OA = OC,OB = OD,把△OCD 绕点 O 旋转 180°,你有什么发现?
在平面内,把一个图形上的每一个点 P 对应到它在绕点 O 旋转 180°下的像 P′,这个变换称为关于点 O 的中心对称.
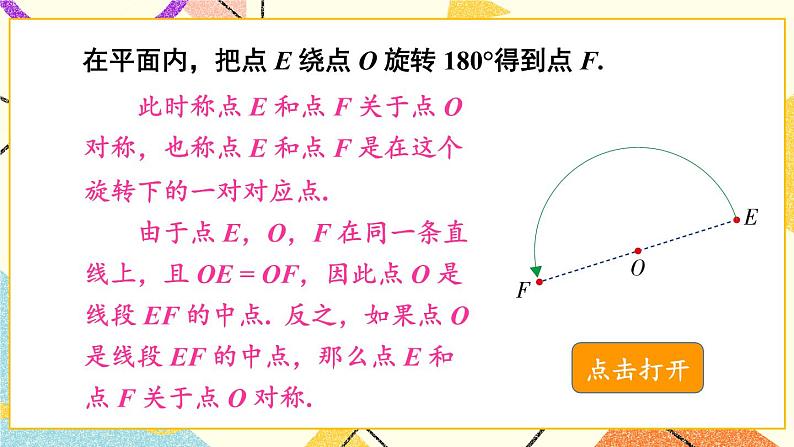
在平面内,把点 E 绕点 O 旋转 180°得到点 F.
此时称点 E 和点 F 关于点 O 对称,也称点 E 和点 F 是在这个旋转下的一对对应点.
由于点 E,O,F 在同一条直线上,且 OE = OF,因此点 O 是线段 EF 的中点. 反之,如果点 O 是线段 EF 的中点,那么点 E 和点 F 关于点 O 对称.
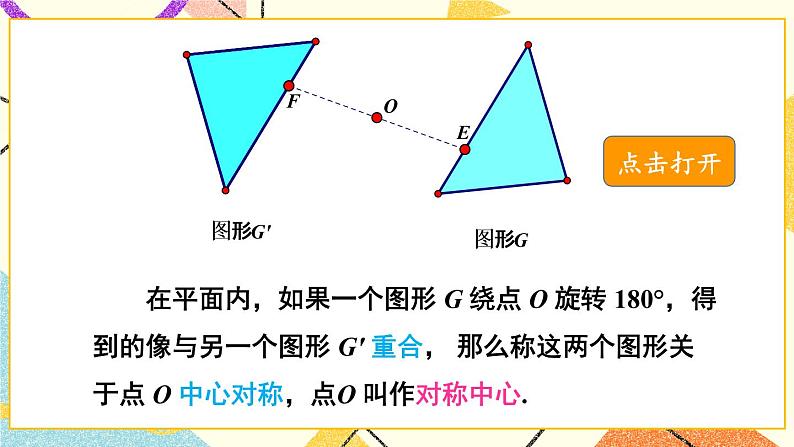
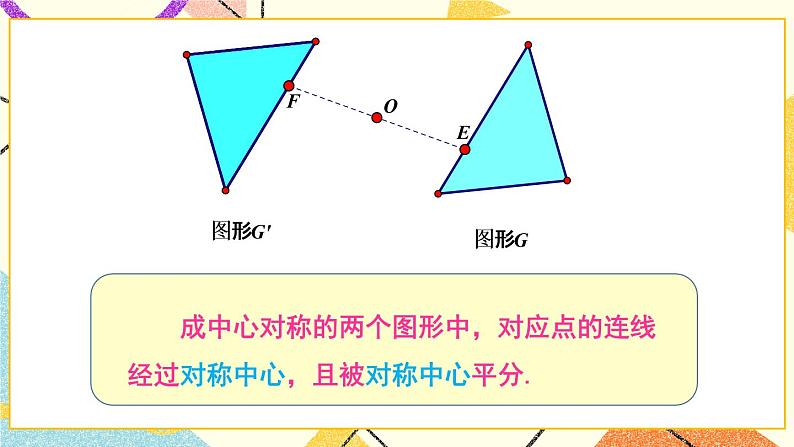
在平面内,如果一个图形 G 绕点 O 旋转 180°,得到的像与另一个图形 G′ 重合, 那么称这两个图形关于点 O 中心对称,点O 叫作对称中心.
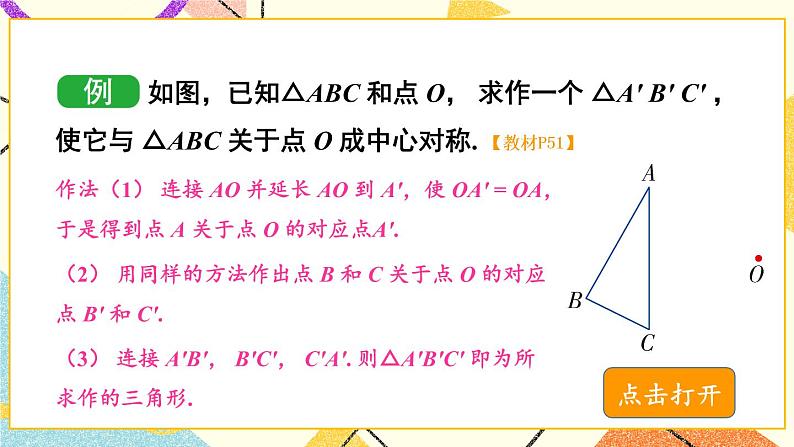
如图,已知△ABC 和点 O, 求作一个 △A′ B′ C′ ,使它与 △ABC 关于点 O 成中心对称.
作法(1) 连接 AO 并延长 AO 到 A′,使 OA′ = OA,于是得到点 A 关于点 O 的对应点A′.
(2) 用同样的方法作出点 B 和 C 关于点 O 的对应点 B′ 和 C′.
(3) 连接 A′B′, B′C′, C′A′. 则△A′B′C′ 即为所求作的三角形.
1. 判断(对的画“√”, 错的画“×”):(1)线段 AB 的中点 O 是点 A 与点 B 的对称中心. ( )(2)等边三角形 ABC 的三条中线的交点是点 A 与 点 B 的对称中心. ( )
2.画出 △ABC 关于点 A 成中心对称的图形.
作法(1) 延长 BA 到 B′,使 AB′ = BA,于是得到点 B 关于点 A 的对应点 B′.
(2) 用同样的方法作出点 C 关于点 A 的对应点 C′.
(3) 连接 C′B′ 则△AB′C′ 即为所求作的三角形.
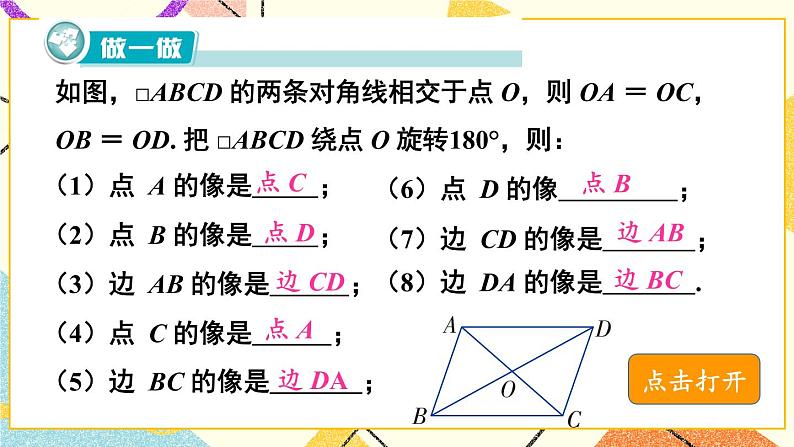
3. 如图,四边形 ABCD 与四边形 A′B′C′D′ 关于某点 中心对称,找出它们的对称中心.
1. 如图, △ABC 和△DEF 关于点 O 成中心对称,要得到 △DEF,需要将△ABC 绕点 O 旋转( )A.30° B.90° C.180° D.360 °
2. 如图,△ABC 与△DEF 关于点 O 成中心对称, 则线段 BC 与 EF 的关系是______________.
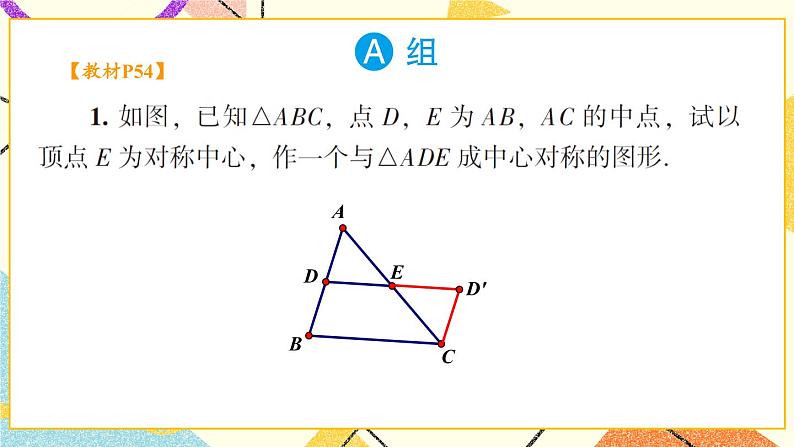
3. 如图,作出与△ABC 关于点 E 成中心对称的图形.
解: 依次寻找点 A , B , C 关于点 E 的对称点, 顺次连接, 所求作图形如图所示:
湘教版八年级下册第2章 四边形2.3 中心对称和中心对称图形优秀ppt课件: 这是一份湘教版八年级下册第2章 四边形2.3 中心对称和中心对称图形优秀ppt课件,文件包含第2课时中心对称图形课件pptx、第1课时中心对称概念及性质课件pptx、23中心对称和中心对称图形练习pptx、第2课时中心对称图形教案doc、第1课时中心对称概念及性质教案doc等5份课件配套教学资源,其中PPT共34页, 欢迎下载使用。
初中北师大版3 平行线的性质一等奖课件ppt: 这是一份初中北师大版3 平行线的性质一等奖课件ppt,文件包含23平行线的性质第2课时pptx、北师大版中学数学七年级下第二章相交线与平行线23平行线的性质第2课时教学详案docx、23平行线的性质第2课时同步练习docx等3份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
湘教版八年级下册2.3 中心对称和中心对称图形一等奖ppt课件: 这是一份湘教版八年级下册2.3 中心对称和中心对称图形一等奖ppt课件,文件包含教学课件八下·湘教·23中心对称和中心对称图形第2课时中心对称图形ppt、23中心对称和中心对称图形第2课时教案docx、23中心对称和中心对称图形第2课时同步练习docx等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。













