沪科版七年级下册8.5 综合与实践 纳米材料的奇异特性完美版课件ppt

这是一份沪科版七年级下册8.5 综合与实践 纳米材料的奇异特性完美版课件ppt，文件包含85综合与实践纳米材料的奇异特性ppt、85综合与实践纳米材料的奇异特性doc等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。
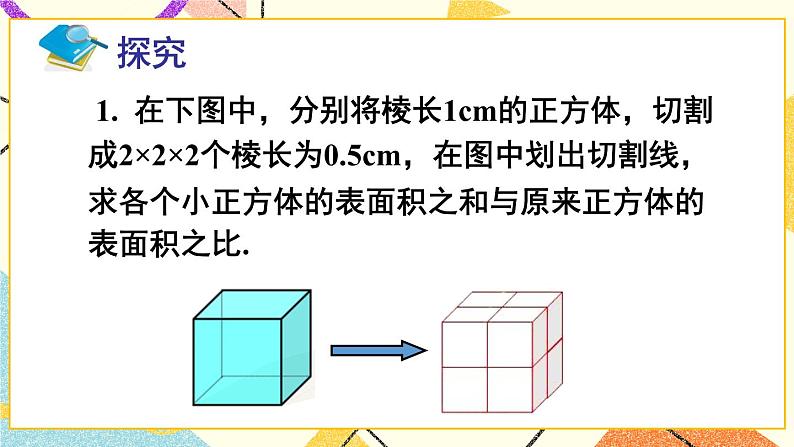
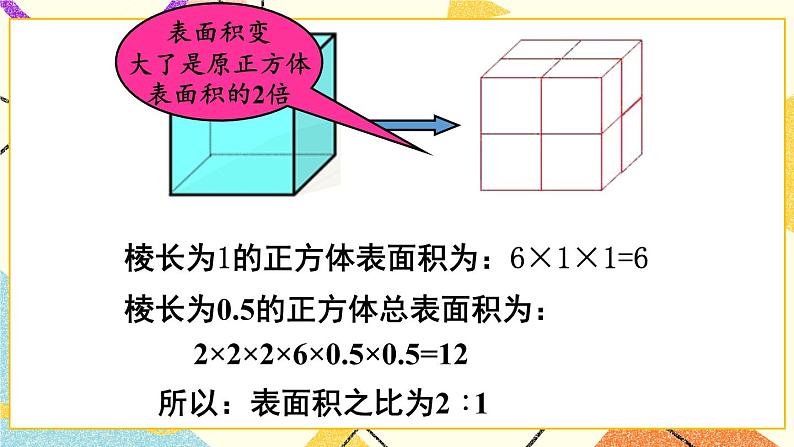
8.5 综合与实践 纳米材料的奇异特性【知识与技能】1.了解纳米材料的一些特性.2.能运用数学知识解决简单实际问题.【过程与方法】从实际问题感受数学与现实世界的紧密联系，体会转化、由特殊到一般等数学思想，培养学生观察、分析和归纳能力.【情感态度】有意识地引导学生积极参与到数学活动过程中，享受运用数学知识解决问题的喜悦，增强学生学好数学的自信心.【教学重点】运用数学知识解决简单实际问题.【教学难点】熟练地运用数学知识解决简单实际问题.一、情境导入，初步认识问题1在图中，分别将边长为1 cm的正方体，切割成2×2×2个边长为0.5 cm和5×5×5个边长为0.2 cm的小正方体，在图中画出切割线.对这两种分割，分别求各小正方体的表面积之和与原正方体的表面积之比.【教学说明】教师提出问题，学生独立思考，然后相互交流，发表各自的见解，在解决问题之前，也可先让学生阅读课本上面的纳米材料的介绍，初步了解纳米材料的奇异特性和形成原因.二、思考探究，获取新知一个正方体进行n×n×n次分解后表面积的变化情况.问题2 将一个边长为1 cm的正方体，切割成n×n×n个边长为cm的小正方体，求各小正方体的表面积之和与原正方体的表面积之比.【教学说明】教师提出问题，学生独立思考，然后相互交流，教师可引导学生从问题1中找到规律，体会由特殊到一般的数学思想.【分析】原正方体的表面积为:6×12=6(cm2).各小正方体的表面积之和为：6×()2×n×n×n=6n(cm2).各小正方体的表面积之和与原正方体的表面积之比为6n÷6=n.问题3说出当n=107（即小正方体边长为1nm）时，各小正方体的表面积之和与原正方体的表面积之比.【教学说明】教师提出问题，学生分析，思考然后相互交流，得出正确答案，体会由一般到特殊的数学思想.【分析】由问题2可知，当n=102时，各小正方体的表面积之和与原正方体的表面积之比为107，即小正方体的表面积之和是原正方体的表面积的107倍.【归纳结论】随着n值的增大，小正方体的长的缩小，各小正方体的表面积之和与原正方体的表面积之比也随之增大.问题4  将问题2中的正方体边长为改为acm，结果如何？【分析】若正方体的边长为acm，则原正方体表面积为：6×a2=6a2(cm2)，各小正方体的表面积之和为:6× ()×n×n×n=6na2(cm2)，各小正方体的表面积之和与原正方体的表面积之比为6na2÷6a2=n.【归纳结论】将一个边长为acm的正方体，切割成n×n×n个边长为cm的小正方体，各小正方体的表面积之和与原正方体的表面积之比为n，即各小正方体的表面积之和是原正方体的表面积的n倍.三、典例精析，掌握新知例1将边长为4cm的正方体切割成20×20×20个边长为0.2cm的小正方体.（1）每个小正方体的表面积是多少？（2）每个小正方体的表面积之和是原正方体表面积的多少倍?【解】（1）0.2×0.2×6=0.24(cm2);（2）各小正方体的表面积之和为：0.24×20×20×20=1920(cm2)原正方体的表面积为：4×4×6=96(cm2)1920÷96=20∴各小正方体的表面积之和是原正方体表面积的20倍.例2 观察：你能写出（a+b)7的展开式吗?【解】展开式中每一项的系数对应着以下规律：【教学说明】教师给出例题，学生尝试独立完成，教师也可让几个学生上台展示自己的答案，交流各自的心得，提高学生解决问题的能力.四、运用新知，深化理解1.将边长为10cm的正方体的细分成棱长为0.5cm的小正方体，可分成的小正方体的个数为（  ）A.20             B.103C.8×102         D.8×1032.将长、宽、高分别是10cm、8cm、6cm的长方体分成棱长为1cm的小正方体.（1）可以分成多少个这样的小正方体？（2）这些小正方体的表面积之比约是原长方体表面积的多少倍？3.如图，101个正方形由小到大套在一起，从外向里相间地画上阴影，最外层画上阴影，最里面的一层画上阴影，最外面的正方形边长为101cm,向里依次为100cm、99cm、…1cm，那么在这个图形中，所有阴影部分的面积之和为多少？【教学说明】教师给出例题，学生独立完成，教师巡视，对学生解题过程中出现的问题及时予以指正，对有困难的学生进行点拨.【答案】1.D2.（1）小正方体的个数为：(10×8×6)÷13=480(个)；（2）小正方体的表面积之和为：12×6×480=2880(cm2)原长方体的表面积为：2×(10×8+10×6+8×6)=376（cm2)2880÷376≈8∴这些小正方体的表面积之和约是原长方体表面积的8倍.3.所有阴影部分的面积之和为：12+(32-22)+(52-42)+(72-62)+……+（1012-1002）=1+5+9+13+…+201=1+2+3+4+5+6+7+…+100+101=5151五、师生互动，课堂小结通过这节课的学习，你掌握了哪些新知识？还有哪些疑问？请与同伴交流.【教学说明】学生相互交流，回顾对一个正方体进行n×n×n次细分后表面积的变化情况，加深对所学新知识的理解和运用.完成练习册中本课时练习.从了解纳米材料的奇异特性，到探究小正方体细分后表面积的变化情况，学生积极主动，体验运用新知解决问题的成就感，增强应用数学的意识.