湖北省孝感市云梦县2022-2023学年八年级上学期期末限时练数学试题（含答案）

云梦县2022-2023学年度上学期期末限时练

八年级数学

一、单选题

1．下列科学防控“新冠肺炎”的图片中，是轴对称图形的为（    ）

A． B． C． D．

2．代数式有意义，则x的取值范围是（    ）

A． B． C． D．且

3．近来，中国芯片技术获得重大突破，芯片已经量产，一举打破以美国为首的西方世界的技术封锁，已知，则0.0000007用科学记数法表示为（    ）

A． B． C． D．

4．下列运算正确的是（    ）

A． B．

C. D．

5．如图，点B、D、E、C在同一直线上，，则（    ）

A． B． C． D．

6．已知，则的值为（    ）

A．10 B．17 C．26 D．33

7．如图，在中，分别以A，C为圆心，大于长为半径作弧，两弧分别相交于M，N两点，作直线，分别交线段，于点D，E，若的周长为，则的周长为（    ）

A． B． C． D．

8．已知甲做360个零件与乙做480个零件所用的天数相同，两人每天共做140个零件，设甲每天做x个零件，根据题意，可列方程为（    ）

A． B． C． D．

二、填空题

9．点关于x轴对称的点Q的坐标为__________．

10．若关于x方程的解是，则a的值为__________．

11．一个多边形的每个内角均为，则这个多边形的边数为__________．

12．计算：（其中且）=__________．

13．如图，已知的周长是22，、分别平分和，于D，且，的面积是__________．

14．已知a，b，c是的三边长，满足，c为偶数，则__________．

15．已知，则__________．

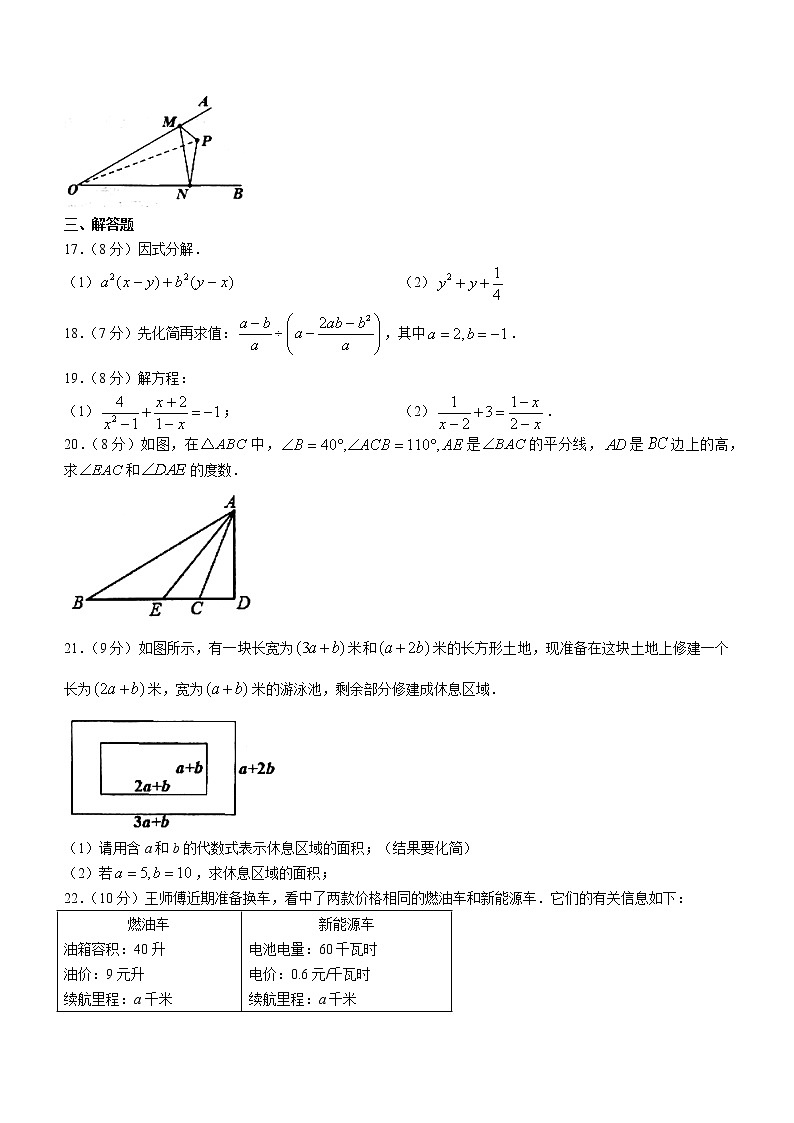
16．如图，已知，P为内一定点；M，N分别是射线，射线上的点，若的周长最小值为6，则__________．

三、解答题

17．（8分）因式分解．

（1） （2）

18．（7分）先化简再求值：，其中．

19．（8分）解方程：

（1）； （2）．

20．（8分）如图，在中，是的平分线，是边上的高，求和的度数．

21．（9分）如图所示，有一块长宽为米和米的长方形土地，现准备在这块土地上修建一个长为米，宽为米的游泳池，剩余部分修建成休息区域．

（1）请用含a和b的代数式表示休息区域的面积；（结果要化简）

（2）若，求休息区域的面积；

22．（10分）王师傅近期准备换车，看中了两款价格相同的燃油车和新能源车．它们的有关信息如下：

（1）用含a的代数式表示新能源车的每千米行驶费用．

（2）若燃油车的每千米行驶费用比新能源车多0.54元．

①分别求出这两款车的每千米行驶费用．

②若燃油车和新能源车每年的其它费用分别为4800元和7500元．问：每年行驶里程超过多少千米时，买新能源车的年费用更低？（年费用=年行驶费用+年其它费用）

23．（10分）如图1，在中，，点D是线段上一点，过B作交于F，连接，过点C作交于点E．

（1）求证：；

（2）如图2，若平分，求证：；

（3）如图3，若为的中线，且，求的长．

24．（12分）如图，在平面直角坐标系中，点A在y轴正半轴上，点B，C在x轴上，，点D在y轴负半轴上，点E在线段上，．

（1）求A、B两点的坐标；

（2）如图1，求证：①；②；

（3）如图2，过点C作，垂足为F，交于点G，若，则点D的坐标为__________．（直接写出结果）

2022-2023学年上学期期末

八年级数学参考答案

1---4：DBAC                5---8：B BCA

9．（－2 ， －6）       10． 4          11．    5           12． 1

13．  33                14． 8          15．    6           16． 6

说明：解答题用非参考答案思路，只要方法正确，请按对应标准给予相应评分

17．解：（1）

，

，                       --------2分

；                  --------4分

（2）

     =             

=                        --------8分

18.解：原式

；                       -------5分      

当a＝2，b＝－1时，

原式．                       -------7分

19.解：（1）方程的两边同时乘以公分母，得：

，                     --------1分

，

解得，                                  --------2分

检验：时,，                     ----------3分

所以原方程的解为．                      ------4分

（2）方程的两边同时乘以公分母，得，

，                          -----5分

，

解得，                                ---------6分

检验：时，,故不是原分式方程的解；-------7分

所以原方程无解．                                  -------8分

20.解：∵在中，∠B=40°，∠ACB=110°

∴            -------2分

∵AE平分∠BAC

∴              ------4分

∵AD是BC上的高

∴∠D=90°                                     ------5分

∴                      -------6分

∴                ------7分

∴∠EAC=15°，∠DAE=35°．                     ------8分

21.解：（1）由题意可得，

休息区域的面积是：    ---------1分

--------2分

，                 ----------4分

即休息区域的面积是：平方米；           --------5分

（2）当，时，

（平方米），       ----------8分

即若，，则休息区域的面积是325平方米；----------9分(掉了单位的扣1分）

22.解：（1）新能源车的每千米行驶费用为元，

答：新能源车的每千米行驶费用为元．            ---------2分

（2）①由题意得：，               ---------3分

解得，                                     ------4分

经检验，是所列分式方程的解，           

则，，             -------6分

答：燃油车的每千米行驶费用为元，新能源车的每千米行驶费用为元；-------7分

②设每年行驶里程为千米时，买新能源车的年费用更低，

由题意得：，                       -------8分

解得，                                            -----9分

答：每年行驶里程超过5000千米时，买新能源车的年费用更低．-------10分

23.（1）证明：如图1中

∵，

∴∠BFD＝90°，∠ECF＝90°

∵∠ACB＝∠BFD＝90°，∠ADC＝∠ BDF，   

∴∠CAE＝∠CBF                 --------2分

∵∠ACE+∠ECD=∠ACD＝90°，∠FCB+∠ECD=∠ECF＝90°

∴∠ACE=∠FCB                 --------3分

又∵

∴（ASA），      --------4分

(2)如图2中，

由（1）可知

∴CF=CE，BF=AE

∵∠ECF＝90°

∴∠CEF＝∠CFE=45°，            ---------5分

∵在Rt△中，，∠

∴∠CAB＝∠CBA=45°，

∵AD平分∠CAB，

∴∠CAE＝22.5°                    ----------6分

那么∠ACE＝∠CE F－∠CAE=45°－22.5°＝22.5°

∴∠CAE=∠ACE                  

∴AE=CE，

∴BF=CF                          ----------7分

(3)解：如图3中，作CH⊥EF于H．  ----------8分

由（2）可知CF=CE

∴EH=HF，

在 ，

∴（AAS），       -------9分

∴ HD=DF

∴ HF=2DF

∴．  ----------10分

24.（1）解： ，，

，     -------1分

∴∠ABO＝90°－∠BAO=30°，                               -------2分

∴                                         -------3分

，，，                                  -------5分

（2）证明：①如图1中，

，，

，

，                               --------6分

，

∴∠ABD＝∠CED，                                    --------7分

②连接．

，，

，

，                                  -------8分

，

，

，                                  -------9分

，    

，

；                                         -------10分

（3）答案：D                                --------12分

解：如图2中，连接，，．

，，

，

（等腰三角形的三线合一），

由（2）可知，，

，

，

，

，

，

，

，

，

又∵DB=DC，

，

，

，

，

，

．