资料中包含下列文件,点击文件名可预览资料内容









还剩15页未读,
继续阅读
所属成套资源:湘教版数学初三下学期PPT课件(送教案)整套
成套系列资料,整套一键下载
4.2.1 概率的概念 课件+教案
展开
这是一份4.2.1 概率的概念 课件+教案,文件包含421概率的概念课件ppt、421概率的概念教案doc等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
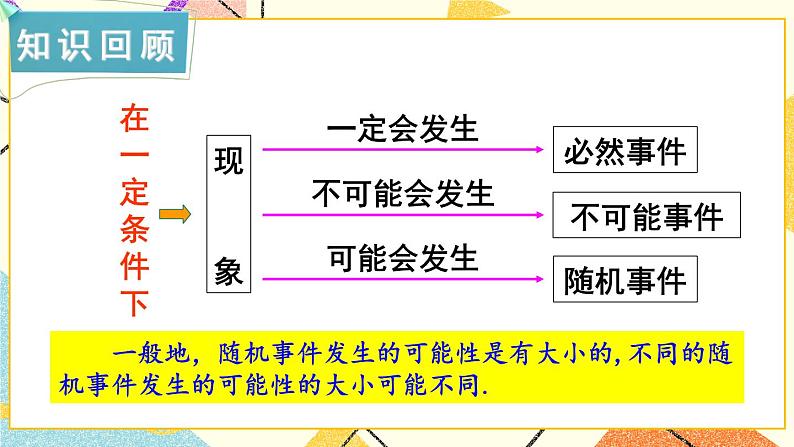
概率的概念湘教·九年级下册知识回顾现象必然事件不可能事件随机事件 一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小可能不同.思考:在同样的条件下, 某一随机事件可能发生也可能不发生,那么,它发生的可能性究竟有多大? 能否用数值来进行刻画呢?探究新知问题1:在一个箱子里放有1个白球和1个红球,它们除颜色外,大小、质地都相同,从袋子中随机取出1个球.问:(1)摸出的球可能是哪个球?(2)全部可能结果有几种?(3)每种结果的可能性大小如何?分析:从箱子中随机取出1个球, 它可能是红球也可能是白球,全部的结果有2种. 由于球的大小和质地都相同,又是随机摸取, 所以每个球被取到的可能性是一样大的.问题2:如图是一个能自由转动的游戏转盘,红、黄、绿3个扇形的圆心角均为120°,让转盘自由转动,当它停止后,问:(1)指针可能停在哪个扇形区域?(2)全部可能结果有几种?(3)每种结果的可能大小如何?红、黄、绿3种由于每个扇形的圆心角度数相等, 对指针指向“红色区域”“黄色区域”“绿色区域” 这3个事件, 发生的条件完全相同, 所以出现每种情况的可能性大小相等. 上述例子和其他大量例子表明,在随机现象中,出现的每一个结果的可能性大小, 能够用一个不超过1的非负数来刻画.概率的定义: 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记为P(A). 把分别写有数字1、2、3、4、5的5张一样的小纸片捻成小纸团放进盒子里,摇匀后,随机取出一个小纸团,试问:(1)取出的序号可能出现几种结果?每个序号数字取出的可能性一样吗?(2)“取出数字3”是什么事件?它的概率是多少?5种,1、2、3、4、5. 可能性相等. 把分别写有数字1、2、3、4、5的5张一样的小纸片捻成小纸团放进盒子里,摇匀后,随机取出一个小纸团,试问:(3)“取出数字小于4”是什么事件?它的概率是多少?(4)“取出数字小于6”是什么事件?它的概率是多少? 把分别写有数字1、2、3、4、5的5张一样的小纸片,捻成小纸团放进盒子里,摇匀后,随机取出一个小纸团,试问:(5)“取出数字6”是什么事件?它的概率是多少?如果事件A包含其中的m种可能结果,那么事件A发生的概率事件A包含的可能结果数一次试验所有可能出现的结果数0≤m≤n特别地,当A为必然事件时,P(A)=1 当A为不可能事件时,P(A)=0事件发生的概率越大,则该事件就越有可能发生,不可能事件必然事件事件发生的可能性越来越大概率为0概率为1事件发生的可能性越来越小 假定按同一种方式掷两枚均匀硬币, 如果第一枚出现正面(即正面朝上), 第二枚出现反面, 就记为(正, 反), 如此类推(如图).(1)写出掷两枚硬币的所有可能结果.解 掷两枚均匀硬币, 所有可能的结果有4个,即(正,正),(正,反),(反,正),(反,反),而且这4 个结果出现的可能性相等. 假定按同一种方式掷两枚均匀硬币, 如果第一枚出现正面(即正面朝上), 第二枚出现反面, 就记为(正, 反), 如此类推(如图).(2)写出下列随机事件发生的所有可能结果.A:“两枚都出现反面”;B:“一枚出现正面、一枚出现反面”;C: “至少有一枚出现反面”.(反,反)(正,反),(反,正)(正,反),(反,正),(反,反) 假定按同一种方式掷两枚均匀硬币, 如果第一枚出现正面(即正面朝上), 第二枚出现反面, 就记为(正, 反), 如此类推(如图).(3)求事件A、B、C的概率.由(1)、(2)可知,练习1. 掷一枚均匀的骰子,骰子的6个面上分别刻有1, 2, 3, 4, 5,6点, 求下列事件的概率:(1)点数为3;(2)点数为偶数;(3)点数为7;(4)点数大于2小于6.练习2. 一只自由飞行的小鸟,将随意地落在如图所示的方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为___________.随堂练习1.如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )A. B. C. D.D2.如图,一个圆形转盘被分成6个圆心角都为60°的扇形,任意转动这个转盘1次,当转盘停止转动时,指针指向阴影区域的概率是( )A. B. C. D.D3.已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同,若从该布袋里任意摸出1个球,是红球的概率为 ,则a等于( )A. 1 B. 2 C.3 D.4A4.如图是一副普通扑克牌中的13张黑桃牌.将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于9的概率为_______.5. 100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是________.6.如掷一个骰子,观察向上的一面的点数,求下列事件的概率:(1)点数为2;(2)点数为奇数;(3)点数大于2且小于5.课堂小结事件A包含的可能结果数一次试验所有可能出现的结果数0≤m≤n不可能事件必然事件事件发生的可能性越来越大概率为0概率为1事件发生的可能性越来越小课后作业1.从课后习题中选取;2.完成练习册本课时的习题.
概率的概念湘教·九年级下册知识回顾现象必然事件不可能事件随机事件 一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小可能不同.思考:在同样的条件下, 某一随机事件可能发生也可能不发生,那么,它发生的可能性究竟有多大? 能否用数值来进行刻画呢?探究新知问题1:在一个箱子里放有1个白球和1个红球,它们除颜色外,大小、质地都相同,从袋子中随机取出1个球.问:(1)摸出的球可能是哪个球?(2)全部可能结果有几种?(3)每种结果的可能性大小如何?分析:从箱子中随机取出1个球, 它可能是红球也可能是白球,全部的结果有2种. 由于球的大小和质地都相同,又是随机摸取, 所以每个球被取到的可能性是一样大的.问题2:如图是一个能自由转动的游戏转盘,红、黄、绿3个扇形的圆心角均为120°,让转盘自由转动,当它停止后,问:(1)指针可能停在哪个扇形区域?(2)全部可能结果有几种?(3)每种结果的可能大小如何?红、黄、绿3种由于每个扇形的圆心角度数相等, 对指针指向“红色区域”“黄色区域”“绿色区域” 这3个事件, 发生的条件完全相同, 所以出现每种情况的可能性大小相等. 上述例子和其他大量例子表明,在随机现象中,出现的每一个结果的可能性大小, 能够用一个不超过1的非负数来刻画.概率的定义: 一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记为P(A). 把分别写有数字1、2、3、4、5的5张一样的小纸片捻成小纸团放进盒子里,摇匀后,随机取出一个小纸团,试问:(1)取出的序号可能出现几种结果?每个序号数字取出的可能性一样吗?(2)“取出数字3”是什么事件?它的概率是多少?5种,1、2、3、4、5. 可能性相等. 把分别写有数字1、2、3、4、5的5张一样的小纸片捻成小纸团放进盒子里,摇匀后,随机取出一个小纸团,试问:(3)“取出数字小于4”是什么事件?它的概率是多少?(4)“取出数字小于6”是什么事件?它的概率是多少? 把分别写有数字1、2、3、4、5的5张一样的小纸片,捻成小纸团放进盒子里,摇匀后,随机取出一个小纸团,试问:(5)“取出数字6”是什么事件?它的概率是多少?如果事件A包含其中的m种可能结果,那么事件A发生的概率事件A包含的可能结果数一次试验所有可能出现的结果数0≤m≤n特别地,当A为必然事件时,P(A)=1 当A为不可能事件时,P(A)=0事件发生的概率越大,则该事件就越有可能发生,不可能事件必然事件事件发生的可能性越来越大概率为0概率为1事件发生的可能性越来越小 假定按同一种方式掷两枚均匀硬币, 如果第一枚出现正面(即正面朝上), 第二枚出现反面, 就记为(正, 反), 如此类推(如图).(1)写出掷两枚硬币的所有可能结果.解 掷两枚均匀硬币, 所有可能的结果有4个,即(正,正),(正,反),(反,正),(反,反),而且这4 个结果出现的可能性相等. 假定按同一种方式掷两枚均匀硬币, 如果第一枚出现正面(即正面朝上), 第二枚出现反面, 就记为(正, 反), 如此类推(如图).(2)写出下列随机事件发生的所有可能结果.A:“两枚都出现反面”;B:“一枚出现正面、一枚出现反面”;C: “至少有一枚出现反面”.(反,反)(正,反),(反,正)(正,反),(反,正),(反,反) 假定按同一种方式掷两枚均匀硬币, 如果第一枚出现正面(即正面朝上), 第二枚出现反面, 就记为(正, 反), 如此类推(如图).(3)求事件A、B、C的概率.由(1)、(2)可知,练习1. 掷一枚均匀的骰子,骰子的6个面上分别刻有1, 2, 3, 4, 5,6点, 求下列事件的概率:(1)点数为3;(2)点数为偶数;(3)点数为7;(4)点数大于2小于6.练习2. 一只自由飞行的小鸟,将随意地落在如图所示的方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为___________.随堂练习1.如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )A. B. C. D.D2.如图,一个圆形转盘被分成6个圆心角都为60°的扇形,任意转动这个转盘1次,当转盘停止转动时,指针指向阴影区域的概率是( )A. B. C. D.D3.已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同,若从该布袋里任意摸出1个球,是红球的概率为 ,则a等于( )A. 1 B. 2 C.3 D.4A4.如图是一副普通扑克牌中的13张黑桃牌.将它们洗匀后正面向下放在桌子上,从中任意抽取一张,则抽出的牌点数小于9的概率为_______.5. 100件外观相同的产品中有5件不合格,现从中任意抽取1件进行检测,抽到不合格产品的概率是________.6.如掷一个骰子,观察向上的一面的点数,求下列事件的概率:(1)点数为2;(2)点数为奇数;(3)点数大于2且小于5.课堂小结事件A包含的可能结果数一次试验所有可能出现的结果数0≤m≤n不可能事件必然事件事件发生的可能性越来越大概率为0概率为1事件发生的可能性越来越小课后作业1.从课后习题中选取;2.完成练习册本课时的习题.
相关资料
更多









