


所属成套资源:数学华师大版中考考点经典导学
2022-2023 数学华师大版中考考点经典导学 考点14平面图形与相交线、平行线
展开
这是一份2022-2023 数学华师大版中考考点经典导学 考点14平面图形与相交线、平行线,文件包含2022-2023数学华师大版中考考点经典导学考点14平面图形与相交线平行线解析版docx、2022-2023数学华师大版中考考点经典导学考点14平面图形与相交线平行线原卷版docx等2份学案配套教学资源,其中学案共30页, 欢迎下载使用。
真题演练
一、单选题
1.(2021·山东日照·中考真题)若不等式组的解集是,则的取值范围是( )
A.B.C.D.
2.(2021·山东济南·中考真题)如图,,,平分,则的度数为( )
A.B.C.D.
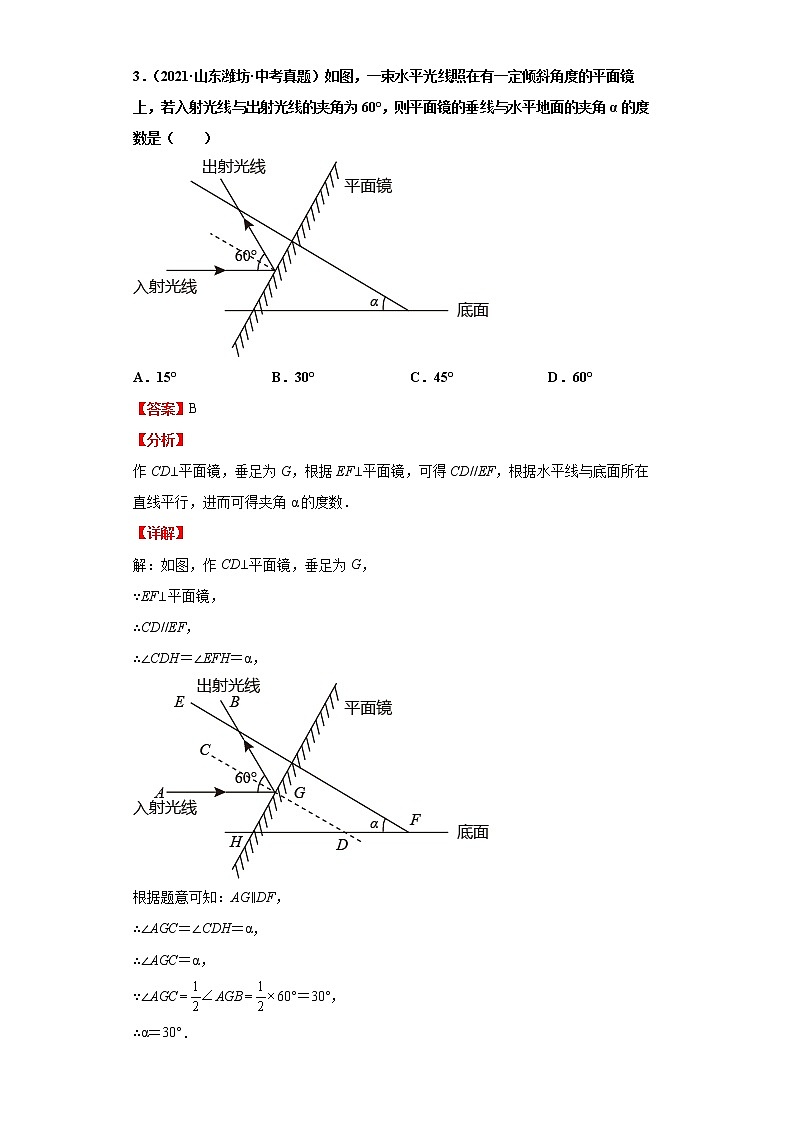
3.(2021·山东潍坊·中考真题)如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是( )
A.15°B.30°C.45°D.60°
4.(2021·山东淄博·中考真题)如图,直线,则等于( )
A.B.C.D.
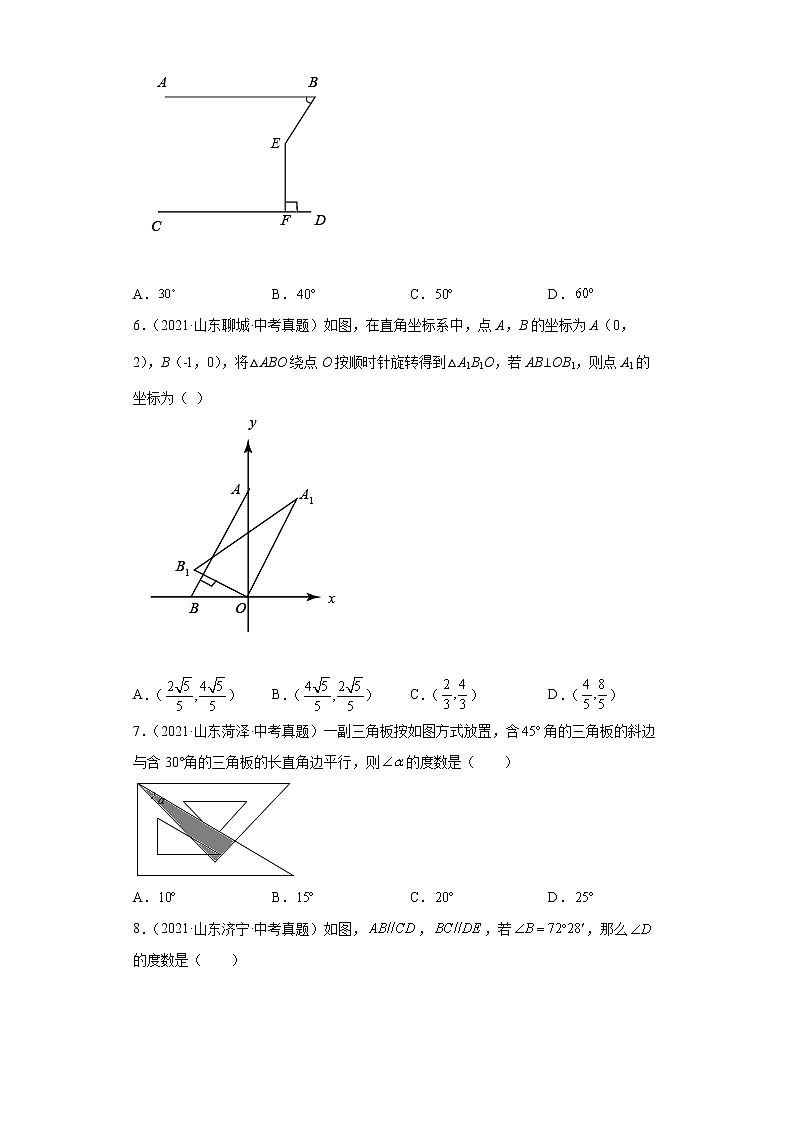
5.(2021·山东东营·中考真题)如图,,于点F,若,则( )
A.B.C.D.
6.(2021·山东聊城·中考真题)如图,在直角坐标系中,点A,B的坐标为A(0,2),B(﹣1,0),将△ABO绕点O按顺时针旋转得到△A1B1O,若AB⊥OB1,则点A1的坐标为( )
A.()B.()C.()D.()
7.(2021·山东菏泽·中考真题)一副三角板按如图方式放置,含角的三角板的斜边与含30°角的三角板的长直角边平行,则的度数是( )
A.B.C.D.
8.(2021·山东济宁·中考真题)如图,,,若,那么的度数是( )
A.B.C.D.
9.(2021·山东聊城·中考真题)如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,则∠CEF的度数为( )
A.95°B.105°C.110°D.115°
10.(2021·山东泰安·中考真题)如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A.B.C.D.
二、填空题
11.(2021·山东滨州·中考真题)如图,在中,,,.若点P是内一点,则的最小值为____________.
12.(2021·山东临沂·中考真题)数学知识在生产和生活中被广泛应用,下列实例所应用的最主要的几何知识,说法正确的是___(只填写序号).
①射击时,瞄准具的缺口、准星和射击目标在同一直线上,应用了“两点确定一条直线”;
②车轮做成圆形,应用了“圆是中心对称图形”;
③学校门口的伸缩门由菱形而不是其他四边形组成,应用了“菱形的对角线互相垂直平分”;
④地板砖可以做成矩形,应用了“矩形对边相等”.
13.(2020·山东聊城·中考真题)如图,在直角坐标系中,点,是第一象限角平分线上的两点,点的纵坐标为1,且,在轴上取一点,连接,,,,使得四边形的周长最小,这个最小周长的值为________.
14.(2020·山东日照·中考真题)如图,有一个含有30°角的直角三角板,一顶点放在直尺的一条边上,若∠2=65°,则∠1的度数是_____.
15.(2021·山东·日照市田家炳实验中学一模)如图,ABC中,点E在AB上,EDBC交∠ABC的平分线于D,交AC于F,若AB=6,BC=5,AE=2,则DF的长为_____.
三、解答题
16.(2021·山东青岛·中考真题)问题提出:
最长边长为128的整数边三角形有多少个?(整数边三角形是指三边长度都是整数的三角形.)
问题探究:
为了探究规律,我们先从最简单的情形入手,从中找到解决问题的方法,最后得出一般性的结论.
(1)如表①,最长边长为1的整数边三角形,显然,最短边长是1,第三边长也是1.按照(最长边长,最短边长,第三边长)的形式记为,有1个,所以总共有个整数边三角形.
表①
(2)如表②,最长边长为2的整数边三角形,最短边长是1或2.根据三角形任意两边之和大于第三边,当最短边长为1时,第三边长只能是2,记为,有1个;当最短边长为2时,显然第三边长也是2,记为,有1个,所以总共有个整数边三角形.
表②
(3)下面在表③中总结最长边长为3的整数边三角形个数情况:
表③
(4)下面在表④中总结最长边长为4的整数边三角形个数情况:
表④
(5)请在表⑤中总结最长边长为5的整数边三角形个数情况并填空:
表⑤
问题解决:
(1)最长边长为6的整数边三角形有___________个.
(2)在整数边三角形中,设最长边长为,总结上述探究过程,当为奇数或为偶数时,整数边三角形个数的规律一样吗?请写出最长边长为的整数边三角形的个数.
(3)最长边长为128的整数边三角形有__________个.
拓展延伸:
在直三棱柱中,若所有棱长均为整数,则最长棱长为9的直三棱柱有___________个.
17.(2021·山东济宁·中考真题)研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.
(1)阅读材料
立体图形中既不相交也不平行的两条直线所成的角,就是将直线平移使其相交所成的角.
例如,正方体(图1).因为在平面中,,与相交于点A,所以直线与所成的就是既不相交也不平行的两条直线与所成的角.
解决问题
如图1,已知正方体,求既不相交也不平行的两条直线与所成角的大小.
(2)如图2,M,N是正方体相邻两个面上的点.
①下列甲、乙、丙三个图形中,只有一个图形可以作为图2的展开图,这个图形是 ;
②在所选正确展开图中,若点M到,的距离分别是2和5,点N到,的距离分别是4和3,P是上一动点,求的最小值.知识点一:直线、线段、射线
关键点拨
1.
基本事实
(1)直线的基本事实:经过两点有且只有一条直线.
(2)线段的基本事实:两点之间,线段最短.
例:在墙壁上固定一根横放的木条,则至少需要2枚钉子,依据的是两点确定一条直线.
知识点二 :角、角平分线
2.概念
(1)角:有公共端点的两条射线组成的图形.
(2)角平分线:在角的内部,以角的顶点为端点把这个角分成两个相等的角的射线
例:
(1)15°25'=15.5°;
37°24'45''+32°48'49''=70°13'34''.
(2)32°的余角是58°,32°的补角是148°.
3.角的度量
1°=60′,1′=60'',1°=3600''
4.余角和补角
( 1 ) 余角:∠1+∠2=90°⇔∠1与∠2互为余角;
( 2 ) 补角:∠1+∠2=180°⇔∠1与∠2互为补角.
(3)性质:同角(或等角)的余角相等;同角(或等角)的补角相等.
知识点三 :相交线、平行线
5.三线八角
(1)同位角:形如”F”;(2)内错角:形如“Z”;(3)同旁内角:形如“U”.
一个角的同位角、内错角或同旁内角可能不止一个,要注意多方位观察
6.对顶角、邻补角
(1)概念:两条直线相交后所得的只有一个公共顶点而没有公共边的两个角叫做对顶角.
(2)性质:对顶角相等,邻补角之和为180°.
例:在平面中,三条直线相交于1点,则图中有6组对顶角.
7.垂线
(1)概念:两条直线互相垂直,其中的一条直线叫做另一条直线的垂线.
(2)性质:①过一点有且只有一条直线与已知直线垂直.
②垂线段最短.
(3)点到直线的距离:直线外一点到这条直线的垂线段的长度
例:如图所示,点 A到BC的距离为AB,点B到AC的距离为BD,点C到AB的距离为BC.
8.平行线
(1)平行线的性质与判定
①同位角相等两直线平行
②内错角相等两直线平行
③同旁内角互补两直线平行
(2)平行公理及其推论
①经过直线外一点,有且只有一条直线与已知直线平行.
②平行于同一条直线的两直线平行.
(1)如果出现两条平行线被其中一条折线所截,那么一般要通过折点作已知直线的平行线.
(2)在平行线的查考时,通常会结合对顶角、角平分线、三角形的内角和以及三角形的外角性质,解题时注意这些性质的综合运用.
知识点四 :命题与证明
9.命题与证明
(1)概念:对某一事件作出正确或不正确判断的语句(或式子)叫做命题,正确的命题称为真命题;错误的命题称为假命题.
(2)命题的结构:由题设和结论两部分组成,命题常写成"如果p,那么q"的形式,其中p是题设,q是结论.
(3)证明:从一个命题的题设出发,通过推理来判断命题是否成立的过程.证明一个命题是假命题时,只要举出一个反例署名命题不成立就可以了.
例:下列命题是假命题的有( ③ )
①相等的角不一定是对顶角;
②同角的补角相等;
③如果某命题是真命题,那么它的逆命题也是真命题;
④若某个命题是定理,则该命题一定是真命题.
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
1
1
1
1个1
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
2
1
1
2个1
2
1
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
3
1
1
2个2
2
,
2
3
1
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
4
1
1
3个2
2
,
2
3
,
2
4
1
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
5
1
1
___
___
2
,
2
3
_______
_____
4
,
2
5
1
相关学案
这是一份2022-2023 数学华师大版中考考点经典导学 考点25概率,文件包含2022-2023数学华师大版中考考点经典导学考点25概率解析版docx、2022-2023数学华师大版中考考点经典导学考点25概率原卷版docx等2份学案配套教学资源,其中学案共26页, 欢迎下载使用。
这是一份2022-2023 数学华师大版中考考点经典导学 考点24视图与投影,文件包含2022-2023数学华师大版中考考点经典导学考点24视图与投影解析版docx、2022-2023数学华师大版中考考点经典导学考点24视图与投影原卷版docx等2份学案配套教学资源,其中学案共18页, 欢迎下载使用。
这是一份2022-2023 数学华师大版中考考点经典导学 考点22与圆有关的计算,文件包含2022-2023数学华师大版中考考点经典导学考点22与圆有关的计算解析版docx、2022-2023数学华师大版中考考点经典导学考点22与圆有关的计算原卷版docx等2份学案配套教学资源,其中学案共26页, 欢迎下载使用。










