贵州省黔东南州2022-2023学年九年级上学期期末考试数学试卷(含答案)

黔东南州2022-2023学年度第一学期期末考试九年级数学试卷

(本试卷共26个小题，满分150分，时间120分钟)

学号         班级         姓名             成绩              

一、选择题：（每题4分，10个小题共40分）

1. 方程的解是  (          )

  A.      B.     C.      D.

2. 用配方法解一元二次方程，变形后的结果正确的是  (           )

   A.    B.   C.    D.

3. 抛物线的顶点坐标为  (            )

   A.（1，3）    B. （-1，3）      C.（1，-3）      D.（-1，-3）

4. 如图，AB是⊙O的切线，A为切点，连接OA、OB，

若∠B＝20°，则∠AOB的度数为  （          ）

A.80°    B.70°     C.60°      D.50°

5. 已知一次函数（为常数）的图象如图所示，则函数的图

象是  (          )

6. 如图，点A、B、C、D都在⊙O上，OA⊥BC，∠CDA＝25°，

则∠OBC等于 （           ）

A.25°     B.30°      C.40°        D.50°    

7. 抛物线先向上平移3个单位，再向右平移1个单位，

所得抛物线的解析式为 (          )

 A.   B.   C.   D.

8. 有两把不同的锁和三把钥匙，其中两把钥匙分别能打开这两把锁，第三把钥匙不能打开这两     

把锁. 随机取出一把钥匙开任意一把锁，一次能打开锁的概率是 （         )

1. 0        B.      C.     D.

9. 如图，△ABC中，∠BAC＝25°，△ABC绕点A逆时针旋

转得到△AED，点B的对应点是点E，连接CD，若AE⊥CD，

则旋转角是（           ）

1. 25°     B. 30°     C.45°        D.50°

10.如图，在边长为6的正方形ABCD内作∠EAF＝45°，AE交BC于点

E，AF交CD于点F，连接EF，将△ADF绕点A顺时针旋转到△ABG

的位置，点D的对应点是点B.若DF＝3，则BE的长为 (           )

1.      B.          C.      D.  2

二、填空题：（每题4分，10个小题共40分）

11. 在平面直角坐标系中，点（3，-2）关于原点对称的点的坐标是             .

12. 写出两根分别为3和4的一个一元二次方程                             .

13. 关于的一元二次方程的一个根为1，则它的另一个根是            .

14. 已知二次函数的、的部分对应值如下表所示：

则该二次函数图象的对称轴为直线                  .

15. 如图，⊙O的弦AB＝8，过点O作OP⊥AB于点C，交⊙O于

点P，若OC:CP＝3:2，则⊙O的半径为                  .

16. 抛物线关于轴对称的抛物线的解析式为                        .
17. 一个不透明的袋子中装有两个小球，上面分别写着“1”“2”，除数字外两个小球无其他差别.

从中摸出一个小球，记录数字，放回并摇匀，再从中随机摸出一个小球，记录其数字，那么两次记录数字之和为3的概率是                 .

18. 将等腰直角三角板ACB（∠ACB＝90°）绕点B顺时针方向旋

转15°得到△，若AC＝3，则阴影部分的面积为           .

19. 已知某直角三角形两条边的长分别是一元二次方程.

的两根，则这个直角三角形的第三边的长为                  .

20. 如图，AB是半圆O的直径，点C、D在半圆O上，点D是弧BC的中

点，点P是直径AB上的动点，连接AC. 若AB＝2，∠CAB＝20°，则

PC＋PD的最小值为           .

三、解答题：（6个小题共70分）

21.（12分） 解方程：（1）   （2）

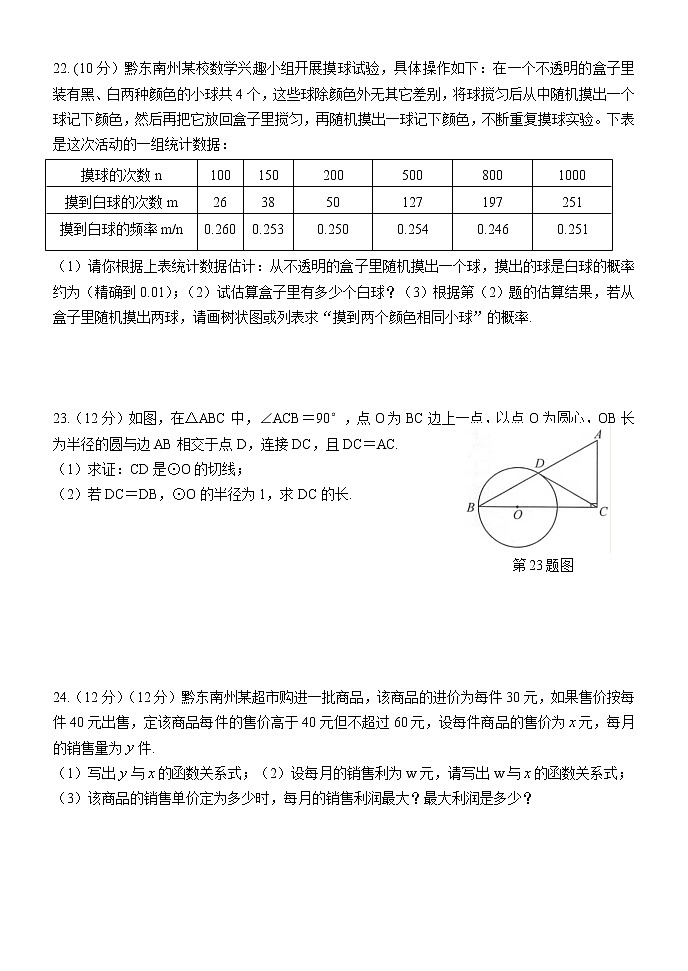
22. (10分）黔东南州某校数学兴趣小组开展摸球试验，具体操作如下：在一个不透明的盒子里装有黑、白两种颜色的小球共4个，这些球除颜色外无其它差别，将球搅匀后从中随机摸出一个球记下颜色，然后再把它放回盒子里搅匀，再随机摸出一球记下颜色，不断重复摸球实验。下表是这次活动的一组统计数据：

（1）请你根据上表统计数据估计：从不透明的盒子里随机摸出一个球，摸出的球是白球的概率约为（精确到0.01）；（2）试估算盒子里有多少个白球？（3）根据第（2）题的估算结果，若从盒子里随机摸出两球，请画树状图或列表求“摸到两个颜色相同小球”的概率.

23.（12分）如图，在△ABC中，∠ACB＝90°，点O为BC边上一点，以点O为圆心，OB长为半径的圆与边AB相交于点D，连接DC，且DC＝AC.

（1）求证：CD是⊙O的切线；

（2）若DC＝DB，⊙O的半径为1，求DC的长.

24.（12分）（12分）黔东南州某超市购进一批商品，该商品的进价为每件30元，如果售价按每件40元出售，定该商品每件的售价高于40元但不超过60元，设每件商品的售价为元，每月的销售量为件.

（1）写出与的函数关系式；（2）设每月的销售利为w元，请写出w与的函数关系式；

（3）该商品的销售单价定为多少时，每月的销售利润最大？最大利润是多少？

25.（12分）如图、抛物线与轴交于A、B两点，与轴交于点C，顶点为D，

其对称轴为直线＝1，且AB＝4.

（1）求抛物线的解析式；（2）连接CD.求证：CD⊥BC；（3）点P是轴上的动点，点Q是直线BC上的动点，是否存在点P、Q，使得以P、Q、C、D四点为顶点的四边形是矩形，若

存在，请求出点P、Q的坐标；若不存在，请说理由.

26. （12分）问题情境：将一副直角三角尺按图①摆放（∠B＝60°，∠F＝45°），等腰直角三角尺EDF的直角边DF恰好垂直平分AB，与AC相交于点G，已知BC＝.

【解决问题】（1）求GC的长；

【猜想证明】（2）如图②，将△DEF绕点D顺时针旋转，使直角边DF经过点C，另一条直角边DE与AC相交于点H，分别过H、C作AB的垂线，垂足分别为M、N.通过观察，猜想MD与ND的数量关系，并证明你的猜想；

【问题拓展】（3）在（2）的条件下，将△DEF沿DB方向平移得到△，当恰好经过（1）中的点G时，请直接写出DD的长度.

黔东南州2022—2023学年度第一学期期末文化水平测试

九年级数学参考答案及评分标准

一、选择题：（每个小题4分，10个小题共40分）

二、填空题：（每个小题4分，10个小题共40分）

11、（-3，2）；12、或（答案不唯一）；13、；14、；15、5；16、；17、；18、；19、4或；20、1.

三、解答题：（6个小题共70分）

21.（12分） 解：（1）

                      =

                      =

      ∴，  …………………………………………6分

（2）原方程可化为：

     ∴，.  …………………………………………12分

22. （10分）解：（1）0.25； …………………………………………2分

设盒子里有个白球，根据题意，得：

解得：

∴盒子里有1个白球.  …………………………………………5分

（3）随机摸出两球的树状图如下：

                                              …………………………………………8分

共有12种等可能结果，而“摸到的两个球是颜色相同的小球”6种结果.

∴  ……………………………………………………………10分

23. （12分）（1）证明：连接OD.

∵OB=OD

∴∠B=∠ODB

∵DC=AC

∴∠A=∠CDA

在△ABC中，∠ACB=90°

∴∠A+∠B=90°

∴∠CDA+∠ODB=90°

∴∠ODC=180°90°，即CD⊥OD

∵OD是半径.

∴CD是⊙O的切线.  …………………………………………6分

（2）连接DE.

∵BE是⊙O的的直径，∴∠BDE=90°

∴∠B+∠BED=90°

∵OD=OE

  ∠ODE=∠OED

∵∠ODC=90°，即∠ODE+∠EDC=90°

∴∠B=∠EDC

∵OB=OD，∴∠DOE=2∠B

∵DC=DB

∴∠B=∠ECD

∴∠B=∠ECD=∠EDC

∴∠OED=2∠ECD

∵∠DOE=2∠B

∴∠OED=∠DOE

∴OD=DE=OE=1

∴

∴DC=DB=  ……………………………………………12分

24. （12分）解：（1），即  ……………………4分

（2），

即  ……………………………………………………………8分

（3）∵

根据题意，知

∵，当时，随的增大而增大.

∴当时，取得最大值为：（元）.

答：该商品的售价定为60元时，每月的销售利润最大，最大利润是6000元.

                                                    …………………………12分

25. （12分）解：(1)∵抛物线的对称轴为直线，且AB=4.

∴A（-1，0）、B（3，0）

∵抛物线与轴交于A、B两点

∴

解得：

∴抛物线的解析式为：.  …………4分

（2）连接BD.

    ∵抛物线与轴交于点C，顶点为D

∴C（0，3）、D（1，4）

∵B（3，0）

∴

∴

∴△BCD为直角三角形，∴CD⊥BC  ………………8分

（3）设直线BC的解析式为：y＝kx＋b

∵B(3，0)、C(0，3)

∴，解得：.

∴直线BC的解析式为：

∵D(1，4)

因此，先将线段CD沿直线CB方向平移，使点D平移后的对应点P在x轴上，点C的对应点Q仍在直线BC上，因为CD⊥BC，因此四边形CQPD              为矩形.此时，点Q的纵坐标为－1.

在中，令，得：x＝4

∴Q(4，－1).   …………………………………10分

∵D(1，4)，∴P(5，0) …………………………………12分

综上，P(5，0)，Q(4，－1).

26. （12分）解：（1）在Rt△ACB中，∠BAC=

∴AB=2BC=，

∵DF垂直平分AB

∴AD=  ………………………1分

设DG=，则AG=

由,得

解得：（负根舍去），只能取

∴AG==4   ………………………3分

∴GC=AC-AG=6-4=2   ……………………4分

（2）MD=ND.证明如下：

∵D是Rt△ACB斜边的中点

∴CD=AD=BD

∵∠B=60°

∴△CDB是等边三角形

∵CN⊥DB

∴    …………………………6分

∵△CDB是等边三角形

∴∠CDB=60°

∵∠EDF=90°

∴∠ADH==∠A

∴HA=HD

∵HM⊥AD

∴   …………………………8分

∵AD=BD

∴MD=ND   ……………………………………10分

（3）  …………………………………………12分