2022-2023学年上海市青浦区八年级上册数学期末专项突破模拟卷（AB卷）含解析

这是一份2022-2023学年上海市青浦区八年级上册数学期末专项突破模拟卷（AB卷）含解析，共43页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。

1. 以下列哪组数为边长，可以得到直角三角形的是( )
A. 9，16，25B. 8，15，17C. 6，8，14D. 10，12，13
2. 在下列各数中是无理数的有( )
－0.333…，，，－π，2.0101001…(相邻两个1之间增加1个0)
A. 3个B. 4个C. 5个D. 2个
3. 如图，直线AB∥ CD，∠ B=50°，∠ C=40°，则∠E等于（ ）
A. 70°B. 80°C. 90°D. 100°
4. 函数图象与轴交点的坐标是（ ）
A. (0，2)B. (0，-2)C. (2，0)D. (-2，0)
5. 下列结果错误的是( )
A. ＝2B. 的算术平方根是4
C. 12的算术平方根是D. (－π)2的算术平方根是π
6. 下列没有属于二元方程组是( )
A. B. C. D.
7. 点P(3，-5)关于y轴对称点的坐标是( )
A. (-3，-5)B. (-3，5)C. (3，-5)D. (5，3)
8. 在直角三角形中，若两边长分别为3和4，则第三边的平方为（ ）
A. 25或7B. 25C. 7D. 5
9. 实数a、b在数轴上对应点的位置如图所示，则|a－b|－的结果是( )
A. 2a－bB. b－2aC. bD. －b
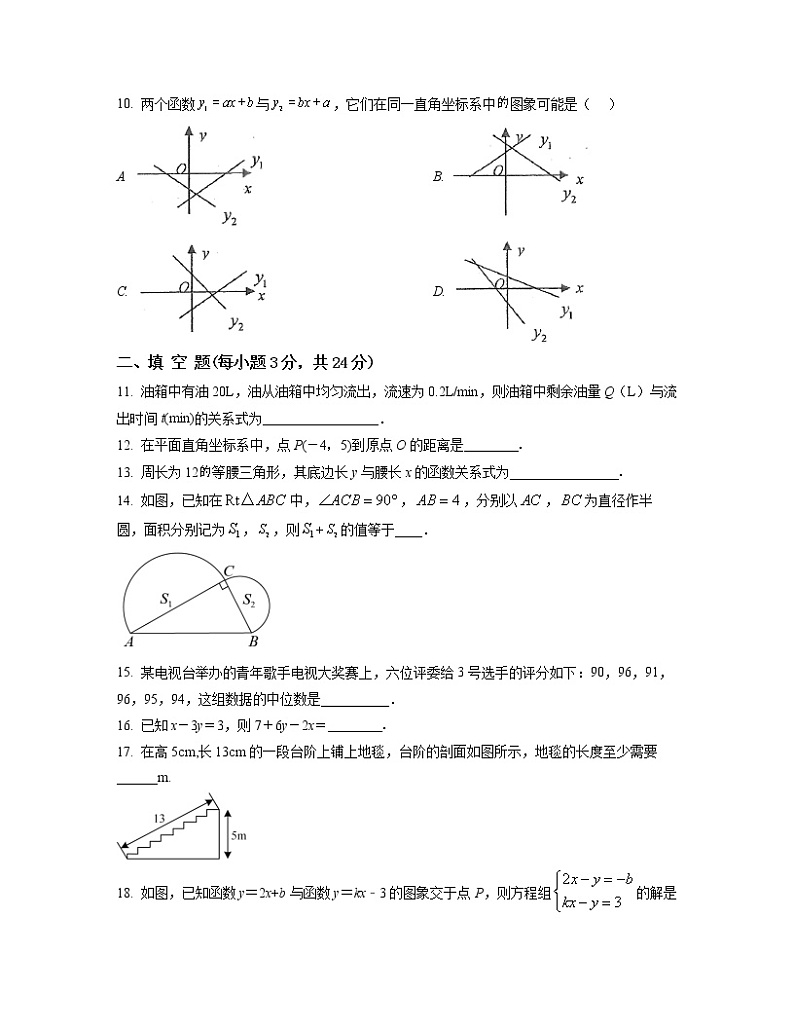
10. 两个函数与，它们在同一直角坐标系中图象可能是（ ）
A B.
C. D.
二、填 空 题(每小题3分，共24分)
11. 油箱中有油20L，油从油箱中均匀流出，流速为0.2L/min，则油箱中剩余油量Q（L）与流出时间t(min)的关系式为_________________．
12. 在平面直角坐标系中，点P(－4，5)到原点O的距离是________．
13. 周长为12等腰三角形，其底边长y与腰长x的函数关系式为________________．
14. 如图，已知在中，，，分别以，为直径作半圆，面积分别记为，，则+的值等于____．
15. 某电视台举办的青年歌手电视大奖赛上，六位评委给3号选手的评分如下：90，96，91，96，95，94，这组数据的中位数是__________．
16. 已知x－3y＝3，则7＋6y－2x＝________．
17. 在高5cm,长13cm的一段台阶上铺上地毯，台阶的剖面如图所示，地毯的长度至少需要______m.
18. 如图，已知函数y＝2x+b与函数y＝kx﹣3的图象交于点P，则方程组的解是______．
三、解 答 题(共66分)
19. 计算：
(1)＋(1－)0； (2)(－)(＋)＋2.
20. 解方程组：
(1)； (2)
21. 如图，已知：DE⊥AO于点E， BO⊥AO于点O，∠CFB=∠EDO，证明：CF∥DO .
22. 某为了解七年级学生一个学期参加综合实践的情况，随机抽样了某校七年级学生一个学期参加综合实践的天数，并用得到的数据绘制了下面两幅没有完整的统计图(如图)，请你根据图中提供的信息，回答下列问题：
(1)求出该校七年级学生总数；
(2)在这次抽样中，众数和中位数分别是多少？

23. “国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网，空气净化器和过滤网在两家商场的售价一样．已知买一个空气净化器和个过滤网要花费元，买个空气净化器和个过滤网要花费元．
（）请用方程组求出一个空气净化器与一个过滤网的价格分别是多少元？
（）为了迎接新年，两家商场都在搞促销，“国美”规定：这两种商品都打九五折；“苏宁”规定：买一个空气净化器奉送两个过滤网．若某单位想要买个空气净化器和个过滤网，如果只能在一家商场购买，请问选择哪家商场购买更合算？请说明理由．
24. 如图信息，L1为船，L2为我公安快艇，航行时路程与时间的函数图象，问
（1）在刚出发时我公安快艇距船多少海里？
（2）计算船与公安快艇的速度分别是多少？
（3）写出L1，L2的解析式
（4）问6分钟时两艇相距几海里．
（5）猜想，公安快艇能否追上船，若能追上，那么在几分钟追上？
25. 台风是一种自然灾害，它以台风为圆心在周围上千米的范围内形成极端气候，有极强的破坏力，有一台风沿东西方向AB由点A行驶向点B，已知点C为一海港，且点C与直线AB上两点A、B的距离分别为300km和400km，又AB＝500km，以台风为圆心周围250km以内为受影响区域．
（1）海港C会受台风影响吗？为什么？
（2）若台风的速度为20km/h，台风影响该海港持续的时间有多长？
2022-2023学年上海市青浦区八年级上册数学期末专项突破模拟卷（A卷）
一、选一选(每小题3分，共30分)
1. 以下列哪组数为边长，可以得到直角三角形的是( )
A. 9，16，25B. 8，15，17C. 6，8，14D. 10，12，13
【正确答案】B
【详解】分析：欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．
详解：A.92+162≠252，故没有为直角三角形；
B.82+152=172，故为直角三角形；
C.62+82≠142，故没有为直角三角形；
D.102+122≠132，故没有为直角三角形.
故选B.
点睛：本题考查了勾股定理的逆定理，关键在于验证两小边的平方和是否等于最长边的平方.
2. 在下列各数中是无理数的有( )
－0.333…，，，－π，2.0101001…(相邻两个1之间增加1个0)
A. 3个B. 4个C. 5个D. 2个
【正确答案】A
【详解】分析：根据无理数的概念判断即可.
详解：无理数有： −π, 2.0101001(相邻两个1之间增加1个0)共有3个.
故选A.
点睛：本题属于概念题，在理解无理数的概念同时，同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限没有循环小数是无理数．
3. 如图，直线AB∥ CD，∠ B=50°，∠ C=40°，则∠E等于（ ）
A. 70°B. 80°C. 90°D. 100°
【正确答案】C
【详解】解：根据平行线的性质得到∠1=∠B=50°，
由三角形的内角和定理可得∠E=180°﹣∠B﹣∠1=90°，
故选C．
本题考查平行线的性质．
4. 函数图象与轴交点的坐标是（ ）
A. (0，2)B. (0，-2)C. (2，0)D. (-2，0)
【正确答案】D
【分析】计算函数值为0所对应的自变量的取值即可．
【详解】解：当y=0时，x+2=0，解得x=-2，
所以函数的图象与x轴的交点坐标为（-2，0）．
故选：D．
本题考查了函数图象与x轴的交点：求出函数值为0时的自变量的值即可得到函数与x轴的交点坐标．
5. 下列结果错误的是( )
A. ＝2B. 的算术平方根是4
C. 12的算术平方根是D. (－π)2的算术平方根是π
【正确答案】B
【详解】分析：依据算术平方根、有理数的乘方法则求解即可．
详解：A. 原式==2，故A正确，与要求没有符；
B.4，4的算术平方根是2，故B错误，与要求相符；
C.12=,它的算术平方根是，故C正确，与要求没有符；
D.(−π)2=π2,π2的算术平方根是π，故D正确，与要求没有符.
故选B.
点睛：本题主要考查了算术平方根，需注意算术平方根只有一个且具有非负性.
6. 下列没有属于二元方程组的是( )
A. B. C. D.
【正确答案】D
【详解】∵含有两个未知数，次数是
∴没有是二元方程.
故选D.
由几个方程组成的一组方程叫做方程组．如果方程组中含有两个未知数，且含未知数的项的次数都是 ，那么这样的方程组叫做二元方程组.
7. 点P(3，-5)关于y轴对称点的坐标是( )
A. (-3，-5)B. (-3，5)C. (3，-5)D. (5，3)
【正确答案】A
【分析】根据关于y轴对称的点的坐标的特点即可得出答案．
【详解】解：由平面直角坐标系中关于y轴对称的点的坐标特点：横坐标相反数，纵坐标没有变，
可得：点P(3，-5)关于y轴的对称点的坐标是（-3，-5）．
故答案选：A．
本题考查了用坐标表示轴对称的知识点，熟练掌握点关于x轴、y轴对称的点的坐标特点是解题的关键．
8. 在直角三角形中，若两边长分别为3和4，则第三边的平方为（ ）
A. 25或7B. 25C. 7D. 5
【正确答案】A
【分析】本题已知直角三角形的两边长，但未明确这两条边是直角边还是斜边，所以求第三边的长必须分类讨论，即4是斜边或直角边的两种情况，然后利用勾股定理求解．
【详解】若4直角边，则第三边x是斜边，由勾股定理，得42+32=x2，所以x2=25；
若4是斜边，则第三边x为直角边，由勾股定理，得x2=42-32，所以x2=7；故x2=25或7．故答案为25或7．
本题考查了利用勾股定理解直角三角形的能力，当已知条件中没有明确哪是斜边时，要注意讨论，一些学生往往忽略这一点，造成丢解．
9. 实数a、b在数轴上对应点的位置如图所示，则|a－b|－的结果是( )
A. 2a－bB. b－2aC. bD. －b
【正确答案】C
【详解】分析：首先由数轴可得a＜b＜0，然后利用二次根式与值的性质，即可求得答案．
详解：根据题意得：a∴a−b<0，
∴|a−b|−=|a−b|−|a|=(b−a)−(−a)=b−a+a=b，
故选C.
点睛：本题考查了实数与数轴，关键在于根据数轴判断出a,b的正负性.
10. 两个函数与，它们在同一直角坐标系中的图象可能是（ ）
A. B.
C. D.
【正确答案】C
【分析】根据函数图象判断a、b的符号，两个函数的图象符号相同即是正确，否则没有正确.
【详解】A、若a>0，b<0，符合，没有符合，故没有符合题意；
B、若a>0，b>0，符合，没有符合，故没有符合题意；
C、若a>0，b<0，符合，符合，故符合题意；
D、若a<0，b>0，符合，没有符合，故没有符合题意；
故选：C.
此题考查函数的性质，能根据函数的解析式y=kx+b中k、b的符号判断函数图象所的象限，当k>0时函数图象过一、三象限，k<0时函数图象过二、四象限；当b>0时与y轴正半轴相交，b<0时与y轴负半轴相交.
二、填 空 题(每小题3分，共24分)
11. 油箱中有油20L，油从油箱中均匀流出，流速为0.2L/min，则油箱中剩余油量Q（L）与流出时间t(min)的关系式为_________________．
【正确答案】Q=20-0.2t
【分析】根据存油量减去用油量，可得答案．
【详解】解：由题意，得
Q=20-0.2t，
故Q=20-0.2t．
本题考查了函数关系式，利用存油量减去用油量是解题关键．
12. 在平面直角坐标系中，点P(－4，5)到原点O的距离是________．
【正确答案】
【分析】直接根据勾股定理计算即可．
【详解】∵P(−4,5)，点O为坐标原点，
过P点作x,y轴垂线，构成直角三角形得
∴OP==.
答：点P到原点的距离是.
故答案为.
本题直接利用勾股定理和点的坐标规律分析解答.关键在于把点的坐标转化到x、y轴的垂线段的长度进而利用勾股定理解答.
13. 周长为12的等腰三角形，其底边长y与腰长x的函数关系式为________________．
【正确答案】y＝12－2x(3＜x＜6)
【详解】分析：根据底边长=周长-2腰长得到函数关系式，根据两腰长＞底边长，底边长＞0可得x的取值范围．
详解：∵等腰三角形的周长为12.
∴ y=12－2x，
又，
解之，得：
3故答案为y＝12－2x(3＜x＜6).
点睛：本题考查了函数关系式，关键在于根据等腰三角形的性质找出其中的等量关系.
14. 如图，已知在中，，，分别以，为直径作半圆，面积分别记为，，则+的值等于____．
【正确答案】2π
【分析】首先把与的表达式列出来，然后求和时根据勾股定理可得到与斜边AB平方的关系，然后得到+的值．
【详解】，，
则+=．
在直角三角形ABC中有：，
则+=．
故2π．
本题考查了勾股定理的综合应用，解题关键在于通过勾股定理建立好两个半圆的面积与斜边的联系．
15. 某电视台举办的青年歌手电视大奖赛上，六位评委给3号选手的评分如下：90，96，91，96，95，94，这组数据的中位数是__________．
【正确答案】94.5
【详解】试题分析：找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．
按从小到大排列为90，91，94，95，96，96
故中位数是按从小到大排列后第三，第四两个数的平均数作为中位数，
故这组数据的中位数是（94+95）=94.5．
考点：本题考查的是中位数
点评：注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求；如果是偶数个则找中间两位数的平均数．
16. 已知x－3y＝3，则7＋6y－2x＝________．
【正确答案】1
【详解】分析：根据等式的性质，可得6y-2x的值，再根据有理数的加法，可得答案．
详解：x−3y=3，
方程两边都乘以−2，得：
6y−2x=−6，方程两边都加7，得：
7+6y−2x=−6+7=1，
故答案为1.
点睛：本题考查了等式的性质：等式两边同时乘以同一个非零数等式没有变；等式两边同时加上同一个数等式没有变.
17. 在高5cm,长13cm的一段台阶上铺上地毯，台阶的剖面如图所示，地毯的长度至少需要______m.
【正确答案】17
【分析】在此类题中，利用平移线段，把楼梯的横竖向下向右平移，构成一个直角三角形的两直角边，利用勾股定理解题．
【详解】利用平移线段，把楼梯的横竖向下向右平移，构成一个直角三角形的两直角边；
则另一直角边长==12，所以地毯的长度为12+5=17米．
故答案：17．
本题主要考查了勾股定理的应用，解决此题的关键是要注意利用平移的知识，把要求的所有线段平移到一条直线上进行计算
18. 如图，已知函数y＝2x+b与函数y＝kx﹣3的图象交于点P，则方程组的解是______．
【正确答案】
【分析】利用“方程组的解就是两个相应的函数图象的交点坐标”解决问题．
【详解】解：∵点P（4，﹣6）为函数y＝2x+b与函数y＝kx﹣3的图象的交点，
∴方程组的解为．
故答案为．
本题考查方程组的解就是两个相应的函数图象的交点坐标，将方程组的解转化为图像的交点问题，属于基础题型．
三、解 答 题(共66分)
19. 计算：
(1)＋(1－)0； (2)(－)(＋)＋2.
【正确答案】(1) 6；(2) 0.
【详解】分析：（1）先提取公因式约分，然后根据零指数幂等于1即可解答.
（2）直接利用平方差公式分解因式求出即可.
详解：（1）原式==6.
（2）原式=.
点睛：本题考查了二次根式的混合运算.难点在于提取公因式及平方差公式的利用.
20. 解方程组：
(1)； (2)
【正确答案】(1) ；(2) .
【详解】分析：直接根据加减消元法即可.
详解：（1），
由①×2+②得：6x=6,解得x=1,
把x=1代入①中得：1-y=4，解得：y=-3.
所以.
（2）,
由①×3+②得：7x=21,解得x=3,
把x=3代入①中得：2×3+y=4，解得：y=-1.
所以.
点睛：本题主要考查了二元方程组的解法：加减消元法，关键在于找出相同字母之间系数的关系.
21. 如图，已知：DE⊥AO于点E， BO⊥AO于点O，∠CFB=∠EDO，证明：CF∥DO .
【正确答案】证明见解析.
【分析】先根据DE⊥AO， BO⊥AO 证明DE∥BO，易证∠BOD=∠CFB就得到CF∥DO .
【详解】证明：∵DE⊥AO，DO⊥AO（已知）
∴（垂直定义）
∴DE∥BO（同位角相等，两条直线平行）
∴∠EDO=∠BOD（两直线平行，内错角相等）
又∵∠EDO=∠CFB（已知）
∴∠BOD=∠CFB（等量代换）
∴CF∥DO（同位角相等，两条直线平行）
考点：平行线的判定，性质.
22. 某为了解七年级学生一个学期参加综合实践的情况，随机抽样了某校七年级学生一个学期参加综合实践的天数，并用得到的数据绘制了下面两幅没有完整的统计图(如图)，请你根据图中提供的信息，回答下列问题：
(1)求出该校七年级学生总数；
(2)在这次抽样中，众数和中位数分别是多少？

【正确答案】(1)总人数为200人；(2)众数是4天，中位数是4天．
【详解】分析：（1）由参加实践为2天的人数除以所占的百分比即可求出八年级学生总数；
（2）出现次数至多的天数为4天，故众数为4；将实践的天数按照从小到大顺序排列，找出最中间的两个天数，求出平均数即可得到中位数；
详解：(1)总人数为20÷10%＝200(人)；
(2)∵a=1-30％-15％-10％-5％-15％=25％，
∴时间为5天七年级学生人数为200×25％=50（人）.
时间为7天的七年级学生人数为200×5%＝10(人)，
由图中的数据可知，4天出现60次，次数至多，所以众数是4天；
数据按从小到大顺序排列，中位数是4天．
点睛：本题考查了中位数，众数，以及样本估计总体.其中需要注意：找中位数需将数据从小到大排列，如果数据为偶数个，取中间两个的平均数；如果数据为奇数个，则直接取中间位数.
23. “国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网，空气净化器和过滤网在两家商场的售价一样．已知买一个空气净化器和个过滤网要花费元，买个空气净化器和个过滤网要花费元．
（）请用方程组求出一个空气净化器与一个过滤网的价格分别是多少元？
（）为了迎接新年，两家商场都在搞促销，“国美”规定：这两种商品都打九五折；“苏宁”规定：买一个空气净化器奉送两个过滤网．若某单位想要买个空气净化器和个过滤网，如果只能在一家商场购买，请问选择哪家商场购买更合算？请说明理由．
【正确答案】（）一个空气净化器元，一个过滤网元；（）苏宁更合算.
【分析】（1）设一个空气净化器 x元，一个过滤网 y元，根据等量关系：1个净化器+1个过滤网=2200，2个净化器+3个过滤网=4760，列方程组即可得解；
（2）分别计算出在每一家需要花费的钱数，比较即可得.
【详解】（）设一个空气净化器元，一个过滤网元，
，
则一个空气净化器元，一个过滤网元．
（）国美：（元），
苏宁：一个净化器送两个过滤网，那么个净化器送个网，只需买个网即可．
∴（元），
∵，
∴苏宁更合算．
24. 如图信息，L1为船，L2为我公安快艇，航行时路程与时间函数图象，问
（1）在刚出发时我公安快艇距船多少海里？
（2）计算船与公安快艇的速度分别是多少？
（3）写出L1，L2的解析式
（4）问6分钟时两艇相距几海里．
（5）猜想，公安快艇能否追上船，若能追上，那么在几分钟追上？
【正确答案】(1)在刚出发时我公安快艇距船5海里；(2)船的速度是1(海里/分)，公安快艇的速度是 (海里/分)；(3) y1＝x＋5，y2＝x；(4) 6分钟时两艇相距2海里；(5) 10分钟时公安快艇追上了船．
【详解】分析：观察图形（1）（2）问很好解决，（3）问中应设出解析式，根据图上给的点确定解析式，代入x=6可求出第4问，第（5）问就是看y1和y2有没有相等情况．
详解：(1)在刚出发时我公安快艇距船5海里．
(2)船的速度是＝1(海里/分)，公安快艇的速度是 (海里/分)．
(3)设L1的解析式为y1＝k1x＋b，将点(0，5)和点(4，9)代入得，
解得.
∴y1＝x＋5.
设L2的解析式为y2＝k2x，将点(4，6)代入得y2＝x.
(4)当x＝6时，y1＝11，y2＝9.11－9＝2(海里)，
∴6分钟时两艇相距2海里．
(5)能追上．令y1＝y2，则x＋5＝x，解得x＝10，
∴10分钟时公安快艇追上了船．
点睛：本题考查了函数的应用，关键在于题意和函数图像正确列出函数关系式.
25. 台风是一种自然灾害，它以台风为圆心在周围上千米的范围内形成极端气候，有极强的破坏力，有一台风沿东西方向AB由点A行驶向点B，已知点C为一海港，且点C与直线AB上两点A、B的距离分别为300km和400km，又AB＝500km，以台风为圆心周围250km以内为受影响区域．
（1）海港C会受台风影响吗？为什么？
（2）若台风的速度为20km/h，台风影响该海港持续的时间有多长？
【正确答案】（1）会，理由见解析；（2）7h
【分析】（1）利用勾股定理的逆定理得出△ABC是直角三角形，进而利用三角形面积得出CD的长，从而判断出海港C是否受台风影响；
（2）利用勾股定理得出ED以及EF的长，进而得出台风影响该海港持续的时间．
【详解】解：（1）如图所示，过点C作CD⊥AB于D点，
∵AC=300km，BC=400km，AB=500km，
∴，
∴△ABC为直角三角形，
∴，
∴，
∴，
∵以台风为圆心周围250km以内为受影响区域，
∴海港C会受到台风影响；
（2）由（1）得CD=240km，
如图所示，当EC=FC=250km时，即台风EF段时，正好影响到海港C，
此时△ECF为等腰三角形，
∵，
∴EF=140km，
∵台风的速度为20km/h，
∴140÷20=7h，
∴台风影响该海港持续的时间有7h．
本题考查的是勾股定理在实际生活中的运用，解答此类题目的关键是构造出直角三角形，再利用勾股定理解答．
2022-2023学年上海市青浦区八年级上册数学期末专项突破模拟卷（B卷）
一、选一选（本题有10小题，每小题3分，满分30分）
1. 下列二次根式中，属于最简二次根式的是（ ）
A. B. C. D.
2. 下列数据是2015年某日发布的北京五个环境监测点PM2.5空气质量指数实时数据：
则这组数据的中位数是（ ）
A. 94B. 96C. 113D. 113.5
3. 在一个直角三角形中，已知两直角边分别为6cm，8cm，则下列结论没有正确的是（ ）
A. 斜边长为10cmB. 周长为25cm
C. 面积为24cm2D. 斜边上的中线长为5cm
4. 如图，▱ABCD中，对角线AC，BD相交于点O，OA＝3，若要使平行四边形ABCD为矩形，则OB长度为（ ）
A. 4B. 3C. 2D. 1
5. 下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差s2:
根据表中数据,要从中进选择一名成绩好又发挥稳定的运动员参加比赛，应该选择( )
A. 乙B. 甲C. 丙D. 丁
6. 下列各命题的逆命题成立的是（ ）
A. 全等三角形的对应角相等
B. 如果两个数相等，那么它们的值相等
C. 对角线互相平分的四边形是平行四边形
D. 如果两个角都是90°，那么这两个角相等
7. 已知直线y=kx+b与y=2x﹣5平行且点（1，3），则y=kx+b的表达式是（ ）
A y=x+2B. y=2x+1C. y=2x+2D. y=2x+3
8. 已知正比例函数，且y随x的增大而减少，则直线的图像是（ ）
A. B.
C. D.
9. 如图，▱ABCD中，AB=4，BC=3，∠DCB=30°，动点E从B点出发，沿B﹣C﹣D﹣A运动至A点停止，设运动的路程为x，△ABE的面积为y，则y与x的函数图象用图象表示正确的是（ ）
A B. C. D.
10. 在平面直角坐标系中，点A（0，4），B（3，0），且四边形ABCD为正方形，若直线l：y=kx+4与线段BC有交点，则k的取值范围是（ ）
A. k≤B. ﹣≤k≤﹣C. ﹣≤k≤﹣1D. ﹣≤k≤
二、填 空 题（共6小题，每小题3分，满分18分）
11. 化简： =__．
12. 如图，▱ABCD中，∠DCE=70°，则∠A=__．
13. 如果菱形有一个内角是60°，周长为32，那么较短对角线长是__．
14. 如图，▱ABCD对角线AC与BD相交于点O，E为BC边中点，已知AB=6cm，则OE的长为__cm．
15. 如图，直线：与直线：相交于点，则关于x的没有等式的解集为______．
16. 如图，在矩形ABCD中的AB边长为6，BC边长为9，E为BC上一点，且CE=2BE，将△ABE翻折得到△AFE，延长EF交AD边于点M，则线段DM的长度为__．
三、解 答 题（共9小题，满分102分，解答要求写出文字说明、证明过程或计算步骤）
17. 计算：（1）﹣+；（2）（）（）﹣（）2．
18. 在大学生一年级新生训练射击比赛中，某小组的成绩如表
（1）该小组射击数据众数是 ．
（2）该小组的平均成绩为多少？（要写出计算过程）
（3）若8环（含8环）以上为射手，在1200名新生中有多少人可以评为射手？
19. 如图，在四边形ABCD中，已知AB=5，BC=3，CD=6，AD=2，若AC⊥BC，求证：AD∥BC．
20. 如图，矩形ABCD中，O为BD中点，PQ过点O分别交AD、BC于点P、Q，连接BP和DQ，求证：四边形PBQD是平行四边形．
21. 如图，已知一条直线点A（5，0）、B（1，4）．
（1）求直线AB的解析式；
（2）若直线y=2x﹣4与直线AB相交于点C，请问直线y=﹣x+4是否也点C？
22. 点A在数轴上，点A所表示的数为，把点A向右平移1个单位得到的点所表示的数为m，把点A向左平移1个单位得到的点所表示的数为n．
（1）直接写出m、n的值：m= ，n= ；
（2）求代数式的值．
23. 甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面．乙队在中途停工了一段时间，然后按停工前的工作效率继续工作．在整个工作过程中，甲队清理完的路面长y（米）与时间x（时）的函数图象为线段OA，乙队铺设完的路面长y（米）与时间x（时）的函数图象为折线BC-CD-DE，如图所示，从甲队开始工作时计时．
（1）分别求线段BC、DE所在直线对应的函数关系式．
（2）当甲队清理完路面时，求乙队铺设完的路面长．
24. 如图，已知直线l：y=﹣x+b与x轴、y轴分别交于点A，B，直线l1：y=x+1与y轴交于点C，设直线l与直线l1的交点为E
（1）如图1，若点E的横坐标为2，求点A的坐标；
（2）在（1）的前提下，D（a，0）为x轴上的一点，过点D作x轴的垂线，分别交直线l与直线l1于点M、N，若以点B、C、M、N为顶点的四边形为平行四边形，求a的值；
（3）如图2，设直线l与直线l2：y=﹣x﹣3的交点为F，问是否存在点B，使BE=BF，若存在，求出直线l的解析式，若没有存在，请说明理由．
25. 已知：矩形ABCD内一点N，△A为等腰直角三角形，连结BN、CN并延长分别交DC，AD于点E，M，在AB上截取BF=EC，连接MF．
（1）求证：四边形FBCE为正方形；
（2）求证：MN=NC；
（3）若S△FMC：S正方形FBCE=2：3，求BN：MD的值．
2022-2023学年上海市青浦区八年级上册数学期末专项突破模拟卷（B卷）
一、选一选（本题有10小题，每小题3分，满分30分）
1. 下列二次根式中，属于最简二次根式的是（ ）
A. B. C. D.
【正确答案】B
【分析】直接利用最简二次根式的定义得出答案．
【详解】解： A、＝5，故此选项错误；
B、是最简二次根式，故此选项正确；
C、＝，故此选项错误；
D、＝2，故此选项错误；
故选B．
此题主要考查了最简二次根式，正确把握最简二次根式的定义是解题关键．
2. 下列数据是2015年某日发布的北京五个环境监测点PM2.5空气质量指数实时数据：
则这组数据的中位数是（ ）
A. 94B. 96C. 113D. 113.5
【正确答案】C
【详解】试题解析：先对这组数据按从小到大的顺序重新排序：94、96、113、114、131．
位于最中间的数是113，
所以这组数中位数是113．
故选C.
3. 在一个直角三角形中，已知两直角边分别为6cm，8cm，则下列结论没有正确的是（ ）
A. 斜边长为10cmB. 周长为25cm
C. 面积为24cm2D. 斜边上的中线长为5cm
【正确答案】B
【详解】试题解析：∵在一个直角三角形中，已知两直角边分别为6cm，8cm，
∴直角三角形的面积=×6×8=24cm2，故选项C没有符合题意；
∴斜边 故选项A没有符合题意；
∴斜边上的中线长为5cm，故选项D没有符合题意；
∵三边长分别为6cm，8cm，10cm，
∴三角形的周长=24cm，故选项B符合题意，
故选B．
点睛：直角三角形斜边的中线等于斜边的一半.
4. 如图，▱ABCD中，对角线AC，BD相交于点O，OA＝3，若要使平行四边形ABCD为矩形，则OB的长度为（ ）
A. 4B. 3C. 2D. 1
【正确答案】B
【详解】试题解析：假如平行四边形ABCD是矩形，
OA=OC，OB=OD，AC=BD，
∴OA=OB=3．
故选B．
点睛：对角线相等的平行四边形是矩形.
5. 下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差s2:
根据表中数据,要从中进选择一名成绩好又发挥稳定的运动员参加比赛，应该选择( )
A. 乙B. 甲C. 丙D. 丁
【正确答案】B
【分析】根据方差的意义先比较出甲、乙、丙、丁的大小，再根据平均数的意义即可求出答案．
【详解】∵=3.5，=3.5，=12.5，=15，
∴=＜＜，
∵=175，=173，.
＞，
∴从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择甲，
故选B．
本题考查了平均数和方差，一般地设n个数据，x1，x2，…xn的平均数为，则方差，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
6. 下列各命题的逆命题成立的是（ ）
A. 全等三角形的对应角相等
B. 如果两个数相等，那么它们的值相等
C. 对角线互相平分的四边形是平行四边形
D. 如果两个角都是90°，那么这两个角相等
【正确答案】C
【详解】A、全等三角形的对应角相等的逆命题是：对应角相等的三角形是全等三角形，错误；
B、如果两个数相等，那么它们的值相等的逆命题是如果两个数的值相等，那么这两个数相等，错误；
C、对角线互相平分的四边形是平行四边形的逆命题是平行四边形的对角线互相平分，正确；
D、如果两个角都是90°，那么这两个角相等的逆命题是如果这两个角相等，那么这两个角都是90°，错误；
故选C．
7. 已知直线y=kx+b与y=2x﹣5平行且点（1，3），则y=kx+b的表达式是（ ）
A. y=x+2B. y=2x+1C. y=2x+2D. y=2x+3
【正确答案】B
【详解】试题解析：∵直线与平行，
把代入得 解得
∴的表达式是
故选B．
8. 已知正比例函数，且y随x的增大而减少，则直线的图像是（ ）
A. B.
C. D.
【正确答案】D
【分析】根据正比例函数的性质可得k﹤0，再根据函数的图象与性质即可做出选择．
【详解】解：∵正比例函数，且y随x的增大而减少，
∴k﹤0，
在中，
∵2﹥0，k﹤0，
∴直线、三、四象限，
故选：D．
本题考查了正比例函数的性质、函数的图象与性质，熟知函数的图象与性质是解答的关键．
9. 如图，▱ABCD中，AB=4，BC=3，∠DCB=30°，动点E从B点出发，沿B﹣C﹣D﹣A运动至A点停止，设运动的路程为x，△ABE的面积为y，则y与x的函数图象用图象表示正确的是（ ）
A. B. C. D.
【正确答案】D
【详解】解：当点E在BC上运动时，三角形的面积没有断增大，面积
当点E在DC上运动时，三角形的面积为定值3．
当点E在AD上运动时三角形的面没有断减小，当点E与点A重合时，面积为0．
故选：D．
10. 在平面直角坐标系中，点A（0，4），B（3，0），且四边形ABCD为正方形，若直线l：y=kx+4与线段BC有交点，则k的取值范围是（ ）
A. k≤B. ﹣≤k≤﹣C. ﹣≤k≤﹣1D. ﹣≤k≤
【正确答案】B
【详解】试题解析：∵四边形ABCD为正方形，点
∴C点坐标为
把代入得解得
把代入得 解得
所以当直线与线段BC有交点时，的取值范围为
故选B．
二、填 空 题（共6小题，每小题3分，满分18分）
11. 化简： =__．
【正确答案】12
【详解】试题解析：
故答案为12.
12. 如图，▱ABCD中，∠DCE=70°，则∠A=__．
【正确答案】110°
【分析】
【详解】解：

在平行四边形中，

故答案为110°．
13. 如果菱形有一个内角是60°，周长为32，那么较短对角线长是__．
【正确答案】8
【详解】试题解析：由菱形的性质可得此菱形的边长为8，
∵菱形的一个内角是60°，
∴60°角所对的对角线与菱形的两边构成的三角形是等边三角形，
故这个菱形较短的对角线长是8．
故答案为8．
14. 如图，▱ABCD的对角线AC与BD相交于点O，E为BC边中点，已知AB=6cm，则OE的长为__cm．
【正确答案】3
【详解】试题解析：在中，
∵点E是BC的中点，
∴是三角形的中位线，

故答案为3．
点睛：三角形的中位线平行于第三边并且等于第三边的一半.
15. 如图，直线：与直线：相交于点，则关于x的没有等式的解集为______．
【正确答案】x≥1
【分析】把点P坐标代入y=x+1中，求得两直线交点坐标，然后根据图像求解．
【详解】解：∵与直线：相交于点，
∴把y=2代入y=x+1中，解得x=1，
∴点P的坐标为（1，2）；
由图可知，x≥1时，．
故x≥1．
本题考查了函数与一元没有等式，待定系数法求函数解析式，联立两直线解析式求交点坐标的方法，求函数与一元没有等式关键在于准确识图，确定出两函数图象的对应的函数值的大小．
16. 如图，在矩形ABCD中的AB边长为6，BC边长为9，E为BC上一点，且CE=2BE，将△ABE翻折得到△AFE，延长EF交AD边于点M，则线段DM的长度为__．
【正确答案】
【详解】试题解析：过M作MN⊥BC于N，
则四边形CDMN是矩形，
∴MN=CD=AB=6，
设DM=x，
∴CN=DM=x，AM=9−x，
∵CE=2BE，
∴BE=3，CE=6，
∴EN=6−x，
∵将△ABE翻折得到△AFE，


∴∠AMF=∠MEN，
在△AMF与△MNE中,
∴△AMF≌△MNE，
∴AF=EM=9−x，



∴DM=
故答案为
三、解 答 题（共9小题，满分102分，解答要求写出文字说明、证明过程或计算步骤）
17. 计算：（1）﹣+；（2）（）（）﹣（）2．
【正确答案】（1）原式=0；（2）原式=﹣2．
【分析】（1）先把各二次根式化为最简二次根式，然后合并即可；
（2）利用平方差公式计算
【详解】（1）原式
（2）原式=5﹣2﹣3=0．
18. 在大学生一年级新生训练射击比赛中，某小组的成绩如表
（1）该小组射击数据的众数是 ．
（2）该小组的平均成绩为多少？（要写出计算过程）
（3）若8环（含8环）以上为射手，在1200名新生中有多少人可以评为射手？
【正确答案】（1）7；（2）该小组的平均成绩为7.4环；（3）在1200名新生中有480人可以评为射手．
【详解】试题分析：（1）根据众数的定义即一组数据中出现次数至多的数，即可得出答案；
（2）根据平均数的计算公式进行计算即可；
（3）用1200乘以选手所占的百分比即可得出答案．
试题解析：（1）∵射击7环数的人数有5个，人数至多，
∴该小组射击数据的众数是7；
故答案为7；
（2）该小组的平均成绩为：（环）；
（3）根据题意得：
（人），
答：在1200名新生中有480人可以评射手．
19. 如图，在四边形ABCD中，已知AB=5，BC=3，CD=6，AD=2，若AC⊥BC，求证：AD∥BC．
【正确答案】证明见解析.
【分析】在中，根据勾股定理求出的值，再在中根据勾股定理的逆定理，判断出AC⊥CD，再根据平行线的判定即可求解．
【详解】证明：在中 根据勾股定理：
∵在中，

∴根据勾股定理的逆定理，为直角三角形，

∴AD∥BC．
20. 如图，矩形ABCD中，O为BD中点，PQ过点O分别交AD、BC于点P、Q，连接BP和DQ，求证：四边形PBQD是平行四边形．
【正确答案】证明见解析
【分析】依据矩形的性质和平行线的性质，通过全等三角形的判定定理判定≌所以 则四边形的对角线互相平分，故四边形为平行四边形．
【详解】∵四边形ABCD是矩形，
∴AD∥BC，
∴∠PDO=∠QBO，
在△POD和△QOB中，

∴△POD≌△QOB(ASA)，
∴OP=OQ；
又∵O为BD的中点，
∴OB=OD，
∴四边形PBQD为平行四边形；
平行四边形的判定：对角线互相平分的四边形是平行四边形
21. 如图，已知一条直线点A（5，0）、B（1，4）．
（1）求直线AB的解析式；
（2）若直线y=2x﹣4与直线AB相交于点C，请问直线y=﹣x+4是否也点C？
【正确答案】（1）直线AB的解析式为y=﹣x+5；（2）直线y=﹣x+4也点C．
【分析】（1）由点A、B的坐标利用待定系数法即可求出直线AB的解析式；
（2）联立两直线解析式成方程组，解方程组得出点C的坐标，再验证点C是否在直线上即可．
【详解】（1）设直线AB的解析式为y=kx+b(k≠0)，
将点A(5,0)、B(1,4)代入y=kx+b中，
得： 解得：
∴直线AB的解析式为y=−x+5
（2）联立两直线解析式得：
解得：
∴点C(3，2)

∴直线也点C
22. 点A在数轴上，点A所表示的数为，把点A向右平移1个单位得到的点所表示的数为m，把点A向左平移1个单位得到的点所表示的数为n．
（1）直接写出m、n的值：m= ，n= ；
（2）求代数式的值．
【正确答案】（1）+1，﹣1；（2）原式=．
【详解】试题分析：（1）向右平移1个单位数字比原来大1，向左平移1个单位数字比原来少1；
（2）将的值代入计算即可．
试题解析：
故答案为
（2）原式


23. 甲、乙两工程队维修同一段路面，甲队先清理路面，乙队在甲队清理后铺设路面．乙队在中途停工了一段时间，然后按停工前的工作效率继续工作．在整个工作过程中，甲队清理完的路面长y（米）与时间x（时）的函数图象为线段OA，乙队铺设完的路面长y（米）与时间x（时）的函数图象为折线BC-CD-DE，如图所示，从甲队开始工作时计时．
（1）分别求线段BC、DE所在直线对应的函数关系式．
（2）当甲队清理完路面时，求乙队铺设完的路面长．
【正确答案】（1）BC所在直线对应的函数关系式为y=25x﹣75．DE所在直线对应的函数关系式为y=25x﹣112.5．（2）乙队铺设完的路面长为87.5米．
【分析】（1）求出乙队铺设路面工作效率，计算出乙队完成需要的时间求出E的坐标，由待定系数法就可以求出结论．
（2）由（1）的结论求出甲队完成的时间，把时间代入乙的解析式就可以求出结论．
【详解】（1）设线段BC所在直线对应函数关系式为y=k1x+b1，
∵图象（3，0）、（5，50），
∴，解得．
∴线段BC所在直线对应的函数关系式为y=25x﹣75．
设线段DE所在直线对应的函数关系式为y=k2x+b2．
∵乙队按停工前的工作效率为：50÷（5﹣3）=25，
∴乙队剩下的需要的时间为：（160﹣50）÷25=．
∴点E的横坐标为6.5+=．∴E（，160）．
∴，解得．
∴线段DE所在直线对应的函数关系式为y=25x﹣112.5．
（2）由题意，得
甲队每小时清理路面的长为 100÷5=20，
甲队清理完路面的时间，x=160÷20=8．
把x=8代入y=25x﹣112.5，得y=25×8﹣112.5=87.5．
答：当甲队清理完路面时，乙队铺设完的路面长为87.5米．
24. 如图，已知直线l：y=﹣x+b与x轴、y轴分别交于点A，B，直线l1：y=x+1与y轴交于点C，设直线l与直线l1的交点为E
（1）如图1，若点E的横坐标为2，求点A的坐标；
（2）在（1）的前提下，D（a，0）为x轴上的一点，过点D作x轴的垂线，分别交直线l与直线l1于点M、N，若以点B、C、M、N为顶点的四边形为平行四边形，求a的值；
（3）如图2，设直线l与直线l2：y=﹣x﹣3的交点为F，问是否存在点B，使BE=BF，若存在，求出直线l的解析式，若没有存在，请说明理由．
【正确答案】（1）点A的坐标为（6，0）；
（2）当以点B、C、M、N为顶点的四边形为平行四边形，a的值为4；
（3）存在点B，使BE=BF，此时直线l的解析式为y=﹣x﹣．
【详解】试题分析：（1）由点E的横坐标函数图象上点的坐标特征即可找出点E的坐标，再利用待定系数法即可求出直线的解析式，令求出的值，即可得出点A的坐标；
（2）根据点D的横坐标为a利用函数图象上点的坐标特征即可找出点M、N的坐标，从而得出线段MN的长度，分别令直线的解析式中求出点的坐标，再根据平行四边形的性质即可得出关于a的含值符号的一元方程，解方程即可得出结论；
（3）假设存在，联立直线的解析式成方程组，解方程组求出点E的坐标，联立直线的解析式成方程组，解方程组求出点F的坐标，即可得出关于b的一元方程，解方程求出b值，此题得解．
试题解析：(1)∵点E在直线l1上，且点E的横坐标为2，
∴点E的坐标为(2,2)，
∵点E在直线l上，
解得：b=3，
∴直线l的解析式为
当y=0时,有
解得：x=6,
∴点A的坐标为(6,0).
(2)依照题意画出图形，如图3所示,
当x=a时，

当x=0时,
∴BC=3−1=2.
∵BC∥MN，
∴当MN=BC=2时，以点B. C. M、N为顶点的四边形为平行四边形，
此时|a−2|=2，
解得：a=4或a=0(舍去).
∴当以点B. C. M、N为顶点的四边形为平行四边形，a的值为4.
(3)假设存在.
联立直线l、l1的解析式成方程组
解得：
∴点E坐标为
联立直线l、l2的解析式成方程
解得：
∴点F的坐标为(18+6b,−9−2b).
∵BE=BF，且E. F均在直线l上，
∴b−1=−18−6b,解得：
此时直线l的解析式为
故存在点B,使BE=BF,此时直线l的解析式为
25. 已知：矩形ABCD内一点N，△A为等腰直角三角形，连结BN、CN并延长分别交DC，AD于点E，M，在AB上截取BF=EC，连接MF．
（1）求证：四边形FBCE为正方形；
（2）求证：MN=NC；
（3）若S△FMC：S正方形FBCE=2：3，求BN：MD的值．
【正确答案】（1）证明见解析；（2）证明见解析；（3）BN：MD=．
【详解】试题分析：（1）先证明四边形为矩形，再利用为等腰直角三角形，证明为等腰直角三角形，则，所以四边形为正方形；
（2）作辅助线，构建全等三角形，证明≌，得，再利用平行线分线段成比例定理可得 则
（3）设 表示出和S正方形FBCE，并根据S△FMC:S正方形FBCE=2:3,依次计算出的长，得结论．
试题解析：(1)如图1，∵四边形ABCD为矩形，
∴AB∥CD,
∴BF∥EC，
∵BF=EC，
∴四边形FBCE为矩形，
∵△A为等腰直角三角形，


∴△BEC为等腰直角三角形,
∴BC=CE，
∴四边形FBCE为正方形；
(2)如图2，过N作GH⊥BC，交BC于H，AD于G，则GH⊥AD，

∴△BHN≌△AGN，
∴NG=NH，
∵AD∥BC，
∴
∴MN=NC；
(3)如图2,设BF=1,则S正方形FBCE=1,，
∵FO=OC，MN=NC，
∴ON∥FM，


由于S△FMC:S正方形FBCE=2:3,
即



∴△AFM是等腰直角三角形，






监测点
A区
B区
C区
D区
E区
PM2.5指数
94
114
96
113
131
甲
乙
丙
丁
平均数
175
173
175
174
方差s2
3.5
3.5
12.5
15
环数
6
7
8
9
人数
1
5
3
1
监测点
A区
B区
C区
D区
E区
PM2.5指数
94
114
96
113
131
甲
乙
丙
丁
平均数
175
173
175
174
方差s2
3.5
3.5
12.5
15
环数
6
7
8
9
人数
1
5
3
1