
还剩19页未读,
继续阅读
成套系列资料,整套一键下载
浙教版初中数学八年级下册第三单元《数据分析初步》(困难)(含答案解析) 试卷
展开
这是一份浙教版初中数学八年级下册第三单元《数据分析初步》(困难)(含答案解析),共22页。
浙教版初中数学八年级下册第三单元《数据分析初步》(困难)(含答案解析)
考试范围:第三单元; 考试时间:120分钟;总分:120分,
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 某同学使用计算器求30个数据的平均数时,错将其中一个数据75输入为15,那么所求出的平均数与实际平均数的差是( )
A. 2.5 B. 2 C. 1 D. −2
2. 为参加全市中学生足球赛.某中学从全校学生中选拔22名足球运动员组建校足球队,这22名运动员的年龄(岁)如下表所示,该足球队队员的平均年龄是( )
年龄(岁)
12
13
14
15
人数
7
10
3
2
A. 12岁 B. 13岁 C. 14岁 D. 15岁
3. 已知数据a1,a2,a3,a4,a5的平均数为k1;a6,a7,a8,a9,a10的平均数为k2.k1与k2的平均数为k,a1,a2,a3,…,a8,a9,a10的平均数为m,那么k与m的大小关系是( )
A. k>m B. k
A. 3.5 B. 3 C. 0.5 D. −3
5. 已知数据4,4,6,6,8,a的中位数是5,如果这组数据有唯一的众数,那么a的值( )
A. 4 B. 6 C. 8 D. 4或6
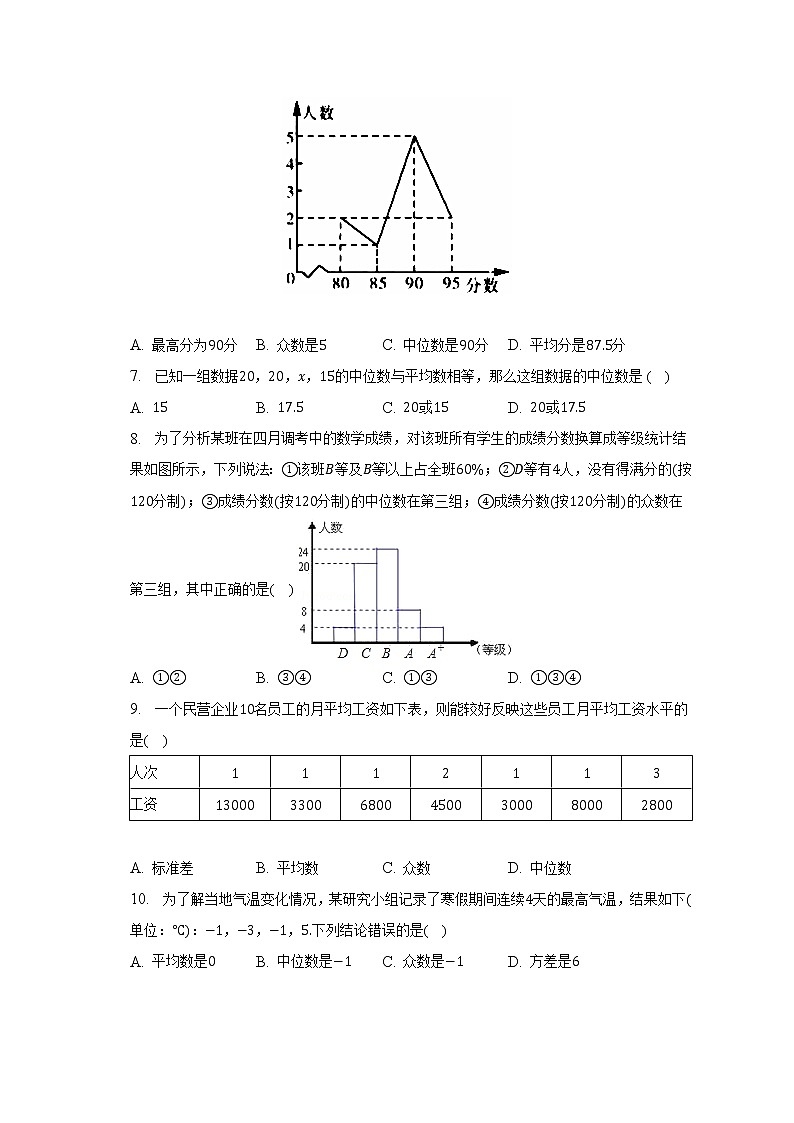
6. 在期中考试中,随机抽取10名学生的数学绘制成折线统计图如图所示,则下列说法正确的是( )
A. 最高分为90分 B. 众数是5 C. 中位数是90分 D. 平均分是87.5分
7. 已知一组数据20,20,x,15的中位数与平均数相等,那么这组数据的中位数是( )
A. 15 B. 17.5 C. 20或15 D. 20或17.5
8. 为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,下列说法:①该班B等及B等以上占全班60%;②D等有4人,没有得满分的(按120分制);③成绩分数(按120分制)的中位数在第三组;④成绩分数(按120分制)的众数在第三组,其中正确的是( )
A. ①② B. ③④ C. ①③ D. ①③④
9. 一个民营企业10名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的是( )
人次
1
1
1
2
1
1
3
工资
13000
3300
6800
4500
3000
8000
2800
A. 标准差 B. 平均数 C. 众数 D. 中位数
10. 为了解当地气温变化情况,某研究小组记录了寒假期间连续4天的最高气温,结果如下(单位:℃):−1,−3,−1,5.下列结论错误的是( )
A. 平均数是0 B. 中位数是−1 C. 众数是−1 D. 方差是6
11. 已知一组数据x1,x2,x3,…,xn的方差为2,则另一组数据3x1,3x2,3x3,…,3xn的方差为 ( )
A. 4 B. 8 C. 16 D. 18
12. 已知样本x1,x2,x3的方差是S2,那么样本3x1,3x2,3x3的方差是( )
A. 3S2 B. 9S2 C. S2 D. S2+3
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13. 十个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个整数,并把自己想好的数如实告诉他两旁的两个人,然后每人将他两旁的人告诉他的数计算出平均数并报出来.已知每个人报的结果如图所示,那么报“3”的人自己心里想的数是______.
14. 某水果店销售11元,18元,24元三种价格的水果,根据水果店一个月这三种水果销售量的统计图(如图),可计算出该店当月销售出水果的平均价格是____元.
15. 某校九年级(1)班40名同学期末考试成绩统计表如下.
成绩x(单位:分)
60≤x<70
70≤x<80
80≤x<90
90≤x≤100
人数
4
14
16
6
下列结论:①成绩的中位数在80≤x<90;②成绩的众数在80≤x<90;③成绩的平均数可能为70;④成绩的极差可能为40.其中所有正确结论的序号是____.
16. 若40个数据的平方和是56,平均数是22,则这组数据的方差______.
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
如图,给出了我国从1998年~2002年每年教育经费投入的情况.
(1)由图可见,1998年~2002年这五年内,我国教育经费投入呈现出______趋势;
(2)根据图中所给数据,求我国1998年~2002年教育经费的年平均数;
(3)如果我国的教育经费从2002年的5480亿元增加到2004年的7891亿元,那么这两年的教育经费平均增长率为多少?(结果精确到0.01)
18. (本小题8.0分)
如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题
(1)这个班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称
白开水
瓶装矿泉水
碳酸饮料
非碳酸饮料
平均价格(元/瓶)
0
2
3
4
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名班委干部(其中有两位班长记为a,b,其余三位记为c,d,e)中随机抽取2名班委干部作良好习惯监督员,请用列表法或画树状图的方法求出恰好抽到2名班长的概率.
19. (本小题8.0分)
附加题:为保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总重量为460克;第二天收集1号电池2节,5号电池3节,总重量为240克.
(1)求1号和5号电池每节分别重多少克?
(2)学校环保小组为估算四月份收集废电池的总重量,他们随意抽取了该月某5天每天收集废电池的数量,如下表:
1号电池(单位:节)
29
30
32
28
31
5号电池(单位:节)
51
53
47
49
50
分别计算两种废电池的样本平均数;并由此估算该月(30天)环保小组收集废电池的总重量是多少千克?
20. (本小题8.0分)
为了了解某中学学生的身高情况,随机对该校男、女生的身高进行抽样调查.抽取的样本中,男、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
组别
男女生身高(cm)
A
150≤x<155
B
155≤x<160
C
160≤x<165
D
165≤x<170
E
170≤x<175
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在______组(填组别序号),女生身高在B组的
有______人;
(2)在样本中,身高在170≤x<175之间的共有______人,人数最多的是______组(填组别序号)
(3)已知该校共有男生500人,女生480人,请估计身高在160≤x<170之间的学生有多少人?
21. (本小题8.0分)
某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元,问平均每人捐款是多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)一一记录下来,则在这组数据中,众数是多少?
22. (本小题8.0分)
某中学有15位学生利用暑假参加社会实践活动,到某公司销售部做某种商品的销售员,销售部为帮助学生制定合理的周销售定额,统计了这15位学生某周的销售量如下:
周销售量(件)
450
130
60
50
40
35
人数
1
1
3
5
3
2
(1)求这15位学生周销售量的平均数、中位数、众数;
(2)假设销售部把每位学生的周销售定额规定为80件,你认为是否合理?为什么?如果不合理,请你从表中选一个较合理的周销售量作为周销售定额,并说明理由.
23. (本小题8.0分)
郴州市飞天山旅游景区上山的一条小路上,有一些断断续续的台阶,如图是其中的甲、乙两段台阶的示意图(每级台阶旁的数字为该级台阶高度,单位为cm).请你用所学过的有关统计知识(平均数、中位数、方差等)回答下列问题:
(1)求甲段台阶高度的中位数和乙段台阶高度的众数;
(2)试问甲、乙哪段台阶更方便游客行走?在台阶数量不变的情况下,如果要将不方便行走的该段台阶进行整修,请你提出合理的整修建议.
24. (本小题8.0分)
一次期中考试中,A,B,C,D,E五位同学的数学、英语成绩有如下信息:
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
2
英语
88
82
94
85
76
85
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩−平均成绩)÷成绩标准差.从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
25. (本小题8.0分)
已知一组数据x1,x2,⋯,x6的平均数为1,方差为53.
(1)求x12+x22+⋯+x62的值;
(2)若在这组数据中加入另一个数据x7,重新计算,平均数无变化,求这7个数据的方差(结果用分数表示).
答案和解析
1.【答案】D
【解析】解:求30个数据的平均数时,错将其中一个数据75输入为15,即使总和减少了60,
那么由此求出的这组数据的平均数与实际平均数的差是−6030=−2;
故选:D.
利用平均数的定义可得.将其中一个数据75输入为15,也就是数据的和少了60,其平均数就少了60除以30,从而得出答案.
本题考查平均数的性质,求数据的平均值和方差是研究数据常做的,平均值反映数据的平均水平,而方差反映数据的波动大小,从两个方面可以准确的把握数据的情况.
2.【答案】B
【解析】解:该足球队队员的平均年龄是12×7+13×10+14×3+15×222=13(岁),
故选:B.
直接利用加权平均数的定义计算可得.
本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
3.【答案】C
【解析】解:∵数据a1,a2,a3,a4,a5的平均数为k1,
∴a1+a2+a3+a4+a5=5k1,
∵a6,a7,a8,a9,a10的平均数为k2,
∴a6+a7+a8+a9+a10=5k2,
∴a1+a2+a3+a4+a5+a6+a7+a8+a9+a10=5k1+5k2,
∴a1,a2,a3,…,a8,a9,a10的平均数为5k1+5k210=k1+k22=m,
∵k1与k2的平均数为k,
∴k=k1+k22,
∴k=m;
故选:C.
先分别求出数据a1,a2,a3,a4,a5和a6,a7,a8,a9,a10的和,根据平均数的计算公式求出a1,a2,a3,…,a8,a9,a10的平均数,再与a1,a2,a3,…,a8,a9,a10的平均数为m进行比较,即可得出答案.
此题考查了加权平均数,用到的知识点是加权平均数的计算公式,关键是根据加权平均数求出总数.
4.【答案】D
【解析】
【分析】
本题考查算术平均数,解题的关键是明确算术平均数的计算方法.根据题意可以得到求出的平均数与实际平均数之间的差值,本题得以解决.
【解答】
解:∵(105−15)÷30=90÷30=3,
∴求出的平均数与实际平均数的差是−3,
故选D.
5.【答案】A
【解析】解:∵4,4,6,6,8,a这组数据有唯一的众数,且4和6都出现两次
∴有a=4或a=6两种情况
当a=4时,这组数据为:4,4,4,6,6,8,中位数为:4+62=5 满足题意.
当a=6时,这组数据为:4,4,6,6,6,8,中位数为:6+62=6≠5,不满足题意,所以a=6舍去.
∴a=4,
故选A.
本题考查了众数和中位数,一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则最中间两个数据的平均数就是这组数据的中位数.
解答本题的关键是熟练掌握中位数和众数的定义.
6.【答案】C
【解析】解:(1)最高分是95分不是90分.
(2)根据众数、中位数的定义可知,众数是90,中位数也是90.
所以正确答案应选C.
故选:C.
认真阅读题意,分析折线图,运用中位数、众数定义来做即可.
考查折线统计图的认识,众数、中位数的定义,关键是对折线统计图的理解和众数、中位数定义的理解.
7.【答案】D
【解析】
【分析】
本题结合平均数考查了确定一组数据的中位数的能力.涉及到分类讨论思想,较难,要明确中位数的值与大小排列顺序有关,一些学生往往对这个概念掌握不清楚,计算方法不明确而解答不完整.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数,因为中位数的值与大小排列顺序有关,而此题中x的大小位置未定,故应该分类讨论x所处的所有位置情况:从小到大(或从大到小)排列在中间(在第二位或第三位结果不影响);结尾;开始的位置.
【解答】
解:(1)将这组数据从大到小的顺序排列后20,20,x,15,处于中间位置的那个数是20,x,
那么由中位数的定义可知,(20+x)÷2=(20+20+x+15)÷4,
x=15,符合题意;中位数为:(20+15)=17.5
(2)将这组数据从大到小的顺序排列后20,20,15,x,中位数是(20+15)÷2=17.5,
此时平均数是(20+20+x+15)÷4=17.5,
x=15,符合题意;
(3)将这组数据从大到小的顺序排列后x,20,20,15,中位数是20,
平均数(20+20+x+15)÷4=20,
x=25,符合题意;
所以中位数是20或17.5.
故选D.
8.【答案】C
【解析】
【分析】
本题考查的是众数,中位数有关知识,根据百分比,中位数,众数的定义对每个问题分别解答,即可确定选项.
【解答】
解:①28+8+44+20+24+8+4×100%=60%,正确,
②D等有4人,但看不出其具体的份数,错误,
③该班共有6人,在D等,C等的义工24人,所以中位数在第三组,正确,
④虽然第三组的人数多,但成绩分数不确定,所以众数不确定,错误.
故选C.
9.【答案】D
【解析】
【分析】
此题主要考查了平均数以及中位数和众数的定义求法和标准差的意义,正确把握相关定义是解题关键.分别利用平均数以及中位数和众数的定义求法和标准差的意义分别分析得出答案.
【解答】
解:平均数为:(13000+3300+6800+4500×2+3000+8000+2800×3)÷10=5150,
中位数是:(3300+4500)÷2=3900,
众数是:2800,
标准差反映的是数据的波动大小,无法反映这些员工月平均工资水平,只有中位数3900,能够较好反映这些员工月平均工资水平.
故选D.
10.【答案】D
【解析】
【分析】
此题考查了方差、平均数、中位数及众数的知识,属于基础题,掌握各部分的定义及计算方法是解题关键.
根据平均数的计算公式、中位数、众数的定义以及方差公式分别对每一项进行分析即可.
【解答】
解:平均数=(−1−3−1+5)÷4=0,
把这些数从小到大排列为:−3,−1,−1,5,
则中位数是−1;
∵数据−1出现两次最多,
∴众数为−1,
方差=14[(5−0)2+2(−1−0)2+(−3−0)2]=9.
故选:D.
11.【答案】D
【解析】
【分析】
此题考查了方差,若一组数据中的各个数据都加上或减去同一个数后得到的新数据的方差与原数据的方差相等;若一组数据中的各个数据都扩大或缩小几倍,则新数据的方差扩大或缩小其平方倍.根据方差的性质,即可计算出3x1,3x2,3x3,…,3xn的方差.
【解答】
解:∵x1,x2,x3,…,xn的方差为2,
又∵一组数据中的各个数据都扩大几倍,则新数据的方差扩大其平方倍,
∴3x1,3x2,3x3,…,3xn的方差为32×2=18,
故选D.
12.【答案】B
【解析】
【分析】
本题考查方差的定义.可以推广到一般的情况即样本中如果每个数据都加上一个数x,则平均值为x+x ,方差不变.如果样本中每个数据都乘以一个数n,这平均值为nx,方差为n2⋅S2.
显然本题样本中的每个数据都乘以3,则平均值为3x,代入方差公式可以求得本题的方差.
【解答】
解:由题意可知:
x1、x2、x3的方差S2=13x1−x2+x2−x2+x3−x2.
样本3x1、3x2、3x3平均值为3x,
则方差S22=133x1−3x2+3x2−3x2+3x3−3x2
=139x1−x2+9x2−x2+9x3−x2
=3x1−x2+x2−x2+x3−x2
=9S2.
故选:B.
13.【答案】−2
【解析】解:设报3的人心里想的数是x,
则报5的人心里想的数应是8−x,
于是报7的人心里想的数是12−(8−x)=4+x,
报9的人心里想的数是16−(4+x)=12−x,
报1的人心里想的数是20−(12−x)=8+x,
报3的人心里想的数是4−(8+x)=−4−x,
所以得x=−4−x,
解得x=−2.
故答案为:−2.
先设报3的人心里想的数,利用平均数的定义表示报5的人心里想的数;报7的人心里想的数;报9的人心里想的数;报1的人心里想的数,最后建立方程,解方程即可.
本题考查了一元一次方程的应用,解答此题的关键是列出方程.
14.【答案】15.3
【解析】解:该店当月销售出水果的平均价格是11×60%+18×15%+24×25%=15.3(元),
故答案为:15.3.
根据加权平均数的计算方法,分别用单价乘以相应的百分比,计算即可得解.
本题考查扇形统计图及加权平均数,解题的关键是掌握扇形统计图直接反映部分占总体的百分比大小及加权平均数的计算公式.
15.【答案】①④
【解析】
【分析】
本题考查了中位数、众数、平均数和极差的概念,根据中位数、众数、平均数和极差的概念分别进行解答,即可得出答案.
【解答】
解:∵共有40名同学,最中间的数是第20和21个数的平均数,
∴成绩的中位数在80≤x<90,
故①正确;
∵无法判断成绩的众数具体是多少,
∴成绩的众数无法判断,
故②不正确;
∵60≤x<70的人数只有4人,∴这40名同学的平均成绩不能为70,故③不正确;
成绩的极差可能为100−60=40,故④正确;
故答案为①④.
16.【答案】0.9
【解析】解:由方差的计算公式可得:
S2=1n[(x1−x−)2+(x2−x−)2+…+(xn−x−)2]
=1n[x12+x22+…+xn2+nx−2−2x−(x1+x2+…+xn)]
=1n[x12+x22+…+xn2+nx−2−2nx−2]=1n[x12+x22+…+xn2]−x−2=5640−12
=1.4−0.5
=0.9.
故填0.9.
根据方差的公式计算即可.方差S2=1n[(x1−x−)2+(x2−x−)2+…+(xn−x−)2].
本题考查方差的计算:一般地设n个数据,x1,x2,…xn的平均数为x−,则方差S2=1n[x12+x22+…+xn2]−x−2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
17.【答案】逐年增长
【解析】解:(1)根据图表可知我国教育经费投入呈现出趋势逐年增长趋势;
(2)根据图表我国教育经费平均数=(2949+3349+3849+4638+5480)÷5=4053亿元;
(3)设这两年的教育经费的平均增长率为x,
则5480(1+x)2=7891
解得x1≈0.20 x2≈−2.2(舍去)(结果精确到0.01)
∴x=0.20=20%.
故答案为(1)逐年增长;
(2)我国1998年~2002年教育经费的年平均数为4053亿元;
(3)教育经费平均增长率为20%.
(1)从图中可以我国从1998年~2002年每年教育经费投入一年比一年高,所以呈现逐年增长的趋势;
(2)我国从1998年~2002年每年教育经费投入分别是2949亿元,3349亿元,3849亿元,4638亿元,5480亿元,所以教育经费的年平均数为(2949+3349+3849+4638+5480)÷5=4053亿元;
(3)第三问考查数量平均变化率问题,解题的关键是正确列出一元二次方程.原来的数量为a,平均每次增长或降低的百分率为x的话,经过第一次调整,就调整到a×(1±x),再经过第二次调整就是a×(1±x)(1±x)=a(1±x)2.增长用“+”,下降用“−”.
本题主要考查的知识点:(1)平均数的求法;(2)涉及一元二次方程的平均变化率的求解.
18.【答案】解:(1)这个班级的学生人数为15÷30%=50(人),
选择C饮品的人数为50−(10+15+5)=20(人),
补全图形如下:
(2)10×0+15×2+20×3+5×450=2.2(元),
答:该班同学每天用于饮品的人均花费是2.2元;
(3)列表如下:
a
b
c
d
e
a
---
(b,a)
(c,a)
(d,a)
(e,a)
b
(a,b)
---
(c,b)
(d,b)
(e,b)
c
(a,c)
(b,c)
---
(d,c)
(e,c)
d
(a,d)
(b,d)
(c,d)
---
(e,d)
e
(a,e)
(b,e)
(c,e)
(d,e)
---
由列表知共有20种等可能结果,其中恰好抽到2名班长的有2种结果,
所以恰好抽到2名班长的概率为220=110.
【解析】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
(1)由B饮品的人数及其所占百分比可得总人数,再根据各饮品的人数之和等于总人数求出C的人数即可补全图形;
(2)根据加权平均数的定义计算可得;
(3)列表得出所有等可能结果,从中找到符合条件的结果,再根据概率公式计算可得.
19.【答案】解:(1)设1号电池每节重x克,5号电池每节重y克,
根据题意得4x+5y=4602x+3y=240
解之得x=90y=20.
(2)∵x−1号=29+30+32+28+315=30(节);x−5号=51+53+47+49+505=50(节)
∴总重量=(30×90+50×20)×30=111(千克).
答:(1)1号和5号电池每节分别重90克,20克;
(2)两种废电池的样本平均数分别为30节,50节.该月(30天)环保小组收集废电池的总重量是111千克.
【解析】根据题意列出方程组求出1号电池和5号电池的重量,然后再利用平均数求出电池的总重量.
解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.学会用样本估计总体的方法也是解决此题的关键.
20.【答案】D 12 10 C
【解析】解:(1)∵在样本中,男生共有2+4+8+12+14=40人,
∴中位数是第20和第21人的平均数,
∴男生身高的中位数落在D组,
女生身高在B组的人数有40×(1−35%−20%−15%−5%)=12人,
故答案为:D、12;
(2)在样本中,身高在170≤x<175之间的人数共有8+40×5%=10人,
∵A组人数为2+40×20%=10人,B组人数为4+12=16人,C组人数为12+40×35%=26人,D组人数为14+40×10%=18人,E组人数为8+40×5%=10人,
∴C组人数最多,
故答案为:10、C;
(3)500×12+1440+480×(35%+10%)=541(人),
故估计身高在160≤x<170之间的学生约有541人.
(1)先求出男生总人数,再根据中位数的定义解答即可,总女生总人数乘以B组的百分比可得;
(2)将位于这一小组内的频数相加,分别计算出各组人数之和即可求得结果;
(3)分别用男、女生的人数乘以对应的百分比,相加即可得解.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
21.【答案】解:(1)参加这次夏令营活动的初中生共有200×(1−10%−20%−30%)=80人;
(2)小学生、高中生和大学生的人数为200×20%=40,200×30%=60,200×10%=20,
所以平均每人捐款=40×5+80×10+60×15+20×20200=11.5(元);
(3)因为初中生最多,所以众数为10(元).
【解析】(1)参加这次夏令营活动的初中生所占比例是:1−10%−20%−30%=40%,就可以求出人数.
(2)小学生、高中生和大学生的人数为200×20%=40,200×30%=60,200×10%=20,根据平均数公式就可以求出平均数.
(3)因为初中生最多,所以众数为初中生捐款数.
本题为统计题,考查了扇形图、加权平均数和众数的含义.提高了学生的综合应用能力,解题时要细心.
22.【答案】解:(1)这15位学生周销售量的平均数=(450×1+130×1+60×3+50×5+40×3+35×2)÷15=80,
中位数为50,众数为50;
(2)不合理.因为15人中有13人销售量达不到80,周销售额定为50较合适,因为50是众数也是中位数.
【解析】(1)根据加权平均数的定义、中位数的定义和众数的定义求解;
(2)由于前面两人的周销售量与其他人相差太大,它们对平均数影响较大,这样用众数中位数50作为周销售定额比较合理.
此题考查了学生对中位数,众数,平均数的掌握情况.它们都是反映数据集中趋势的指标.
23.【答案】解:(1)甲段台阶高度的中位数是15,乙段台阶高度的众数是15;
(2)乙段台阶更方便游客行走,
因为甲路段台阶高度的平均数是15,
所以按每级台阶为15cm的高度进行整修.
【解析】(1)根据中位数和和众数的定义即可求解;
(2)由于要方便游客行走,要重新整修上山的小路,对于这两段台阶路,在台阶数不变的情况下,利用方差的定义即可解决问题.
此题主要考查了方差在实际生活中的应用,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
24.【答案】解:(1)数学平均分是:15×(71+72+…+70)=70分,
英语标准差为:15[(88−85)2+(82−85)2+(94−85)2+(85−85)2+(76−85)2=36=6;
(2)∵数学标准分=71−702=22,英语标准分=88−856=0.5,22>0.5,
∴数学更好.
【解析】(1)由平均数、标准差的公式进行计算即可;
(2)代入公式:标准分=(个人成绩−平均成绩)÷成绩标准差计算,再比较即可.
本题考查的是标准差的计算,计算标准差需要先算出方差,计算方差的步骤是:①计算数据的平均数x−;②计算偏差,即每个数据与平均数的差;③计算偏差的平方和;④偏差的平方和除以数据个数.标准差即方差的算术平方根;注意标准差和方差一样都是非负数.
25.【答案】解:(1)∵数据x1,x2,⋯,x6的平均数为1,
∴x1+x2+⋯+x6=1×6=6,
又∵方差为53,
∴s2=16[(x1−1)2+(x2−1)2+⋯+(x6−1)2]
=16[x12+x22+⋯+x62−2(x1+x2+⋯+x6)+6]
=16(x12+x22+⋯+x62−2×6+6)
=16(x12+x22+⋯+x62)−1=53,
∴x12+x22+⋯+x62=16.
(2)∵数据x1,x2,⋯,x7的平均数为1,
∴x1+x2+⋯+x7=1×7=7,
∵x1+x2+⋯+x6=6,
∴x7=1,
∵16[(x1−1)2+(x2−1)2+⋯+(x6−1)2]=53,
∴(x1−1)2+(x2−1)2+⋯+(x6−1)2=10,
∴s′2=17[(x1−1)2+(x2−1)2+⋯+(x7−1)2]
=17×[10+(1−1)2]
=107.
【解析】
【分析】本题考查了平均数与方差的意义.平均数是指在一组数据中所有数据之和再除以数据的个数.一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.计算公式是:s2=
1
n
[(x1−
x
)2+(x2−
x
)2+…+(xn−
x
)2].
(1)先由数据x1,x2,…x6的平均数为1,得出x1+x2+…+x6=1×6=6,再根据方差为
5
3
,得到S2=
1
6
[(x1−1)2+(x2−1)2+…+(x6−1)2]=
5
3
,利用完全平方公式求出
1
6
(x12+x22+…+x62−2×6+6)=
5
3
,进而求解即可;
(2)先由数据x1,x2,…x7的平均数为1,得出x1+x2+…+x7=1×7=7,而x1+x2+…+x6=6,所以x7=1;再根据
1
6
[(x1−1)2+(x2−1)2+…+(x6−1)2]=
5
3
,得出(x1−1)2+(x2−1)2+…+(x6−1)2=10,然后根据方差的计算公式即可求出这7个数据的方差.
浙教版初中数学八年级下册第三单元《数据分析初步》(困难)(含答案解析)
考试范围:第三单元; 考试时间:120分钟;总分:120分,
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 某同学使用计算器求30个数据的平均数时,错将其中一个数据75输入为15,那么所求出的平均数与实际平均数的差是( )
A. 2.5 B. 2 C. 1 D. −2
2. 为参加全市中学生足球赛.某中学从全校学生中选拔22名足球运动员组建校足球队,这22名运动员的年龄(岁)如下表所示,该足球队队员的平均年龄是( )
年龄(岁)
12
13
14
15
人数
7
10
3
2
A. 12岁 B. 13岁 C. 14岁 D. 15岁
3. 已知数据a1,a2,a3,a4,a5的平均数为k1;a6,a7,a8,a9,a10的平均数为k2.k1与k2的平均数为k,a1,a2,a3,…,a8,a9,a10的平均数为m,那么k与m的大小关系是( )
A. k>m B. k
A. 3.5 B. 3 C. 0.5 D. −3
5. 已知数据4,4,6,6,8,a的中位数是5,如果这组数据有唯一的众数,那么a的值( )
A. 4 B. 6 C. 8 D. 4或6
6. 在期中考试中,随机抽取10名学生的数学绘制成折线统计图如图所示,则下列说法正确的是( )
A. 最高分为90分 B. 众数是5 C. 中位数是90分 D. 平均分是87.5分
7. 已知一组数据20,20,x,15的中位数与平均数相等,那么这组数据的中位数是( )
A. 15 B. 17.5 C. 20或15 D. 20或17.5
8. 为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,下列说法:①该班B等及B等以上占全班60%;②D等有4人,没有得满分的(按120分制);③成绩分数(按120分制)的中位数在第三组;④成绩分数(按120分制)的众数在第三组,其中正确的是( )
A. ①② B. ③④ C. ①③ D. ①③④
9. 一个民营企业10名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的是( )
人次
1
1
1
2
1
1
3
工资
13000
3300
6800
4500
3000
8000
2800
A. 标准差 B. 平均数 C. 众数 D. 中位数
10. 为了解当地气温变化情况,某研究小组记录了寒假期间连续4天的最高气温,结果如下(单位:℃):−1,−3,−1,5.下列结论错误的是( )
A. 平均数是0 B. 中位数是−1 C. 众数是−1 D. 方差是6
11. 已知一组数据x1,x2,x3,…,xn的方差为2,则另一组数据3x1,3x2,3x3,…,3xn的方差为 ( )
A. 4 B. 8 C. 16 D. 18
12. 已知样本x1,x2,x3的方差是S2,那么样本3x1,3x2,3x3的方差是( )
A. 3S2 B. 9S2 C. S2 D. S2+3
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13. 十个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个整数,并把自己想好的数如实告诉他两旁的两个人,然后每人将他两旁的人告诉他的数计算出平均数并报出来.已知每个人报的结果如图所示,那么报“3”的人自己心里想的数是______.
14. 某水果店销售11元,18元,24元三种价格的水果,根据水果店一个月这三种水果销售量的统计图(如图),可计算出该店当月销售出水果的平均价格是____元.
15. 某校九年级(1)班40名同学期末考试成绩统计表如下.
成绩x(单位:分)
60≤x<70
70≤x<80
80≤x<90
90≤x≤100
人数
4
14
16
6
下列结论:①成绩的中位数在80≤x<90;②成绩的众数在80≤x<90;③成绩的平均数可能为70;④成绩的极差可能为40.其中所有正确结论的序号是____.
16. 若40个数据的平方和是56,平均数是22,则这组数据的方差______.
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
如图,给出了我国从1998年~2002年每年教育经费投入的情况.
(1)由图可见,1998年~2002年这五年内,我国教育经费投入呈现出______趋势;
(2)根据图中所给数据,求我国1998年~2002年教育经费的年平均数;
(3)如果我国的教育经费从2002年的5480亿元增加到2004年的7891亿元,那么这两年的教育经费平均增长率为多少?(结果精确到0.01)
18. (本小题8.0分)
如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题
(1)这个班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称
白开水
瓶装矿泉水
碳酸饮料
非碳酸饮料
平均价格(元/瓶)
0
2
3
4
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名班委干部(其中有两位班长记为a,b,其余三位记为c,d,e)中随机抽取2名班委干部作良好习惯监督员,请用列表法或画树状图的方法求出恰好抽到2名班长的概率.
19. (本小题8.0分)
附加题:为保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总重量为460克;第二天收集1号电池2节,5号电池3节,总重量为240克.
(1)求1号和5号电池每节分别重多少克?
(2)学校环保小组为估算四月份收集废电池的总重量,他们随意抽取了该月某5天每天收集废电池的数量,如下表:
1号电池(单位:节)
29
30
32
28
31
5号电池(单位:节)
51
53
47
49
50
分别计算两种废电池的样本平均数;并由此估算该月(30天)环保小组收集废电池的总重量是多少千克?
20. (本小题8.0分)
为了了解某中学学生的身高情况,随机对该校男、女生的身高进行抽样调查.抽取的样本中,男、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
组别
男女生身高(cm)
A
150≤x<155
B
155≤x<160
C
160≤x<165
D
165≤x<170
E
170≤x<175
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在______组(填组别序号),女生身高在B组的
有______人;
(2)在样本中,身高在170≤x<175之间的共有______人,人数最多的是______组(填组别序号)
(3)已知该校共有男生500人,女生480人,请估计身高在160≤x<170之间的学生有多少人?
21. (本小题8.0分)
某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元,问平均每人捐款是多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)一一记录下来,则在这组数据中,众数是多少?
22. (本小题8.0分)
某中学有15位学生利用暑假参加社会实践活动,到某公司销售部做某种商品的销售员,销售部为帮助学生制定合理的周销售定额,统计了这15位学生某周的销售量如下:
周销售量(件)
450
130
60
50
40
35
人数
1
1
3
5
3
2
(1)求这15位学生周销售量的平均数、中位数、众数;
(2)假设销售部把每位学生的周销售定额规定为80件,你认为是否合理?为什么?如果不合理,请你从表中选一个较合理的周销售量作为周销售定额,并说明理由.
23. (本小题8.0分)
郴州市飞天山旅游景区上山的一条小路上,有一些断断续续的台阶,如图是其中的甲、乙两段台阶的示意图(每级台阶旁的数字为该级台阶高度,单位为cm).请你用所学过的有关统计知识(平均数、中位数、方差等)回答下列问题:
(1)求甲段台阶高度的中位数和乙段台阶高度的众数;
(2)试问甲、乙哪段台阶更方便游客行走?在台阶数量不变的情况下,如果要将不方便行走的该段台阶进行整修,请你提出合理的整修建议.
24. (本小题8.0分)
一次期中考试中,A,B,C,D,E五位同学的数学、英语成绩有如下信息:
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70
2
英语
88
82
94
85
76
85
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩−平均成绩)÷成绩标准差.从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
25. (本小题8.0分)
已知一组数据x1,x2,⋯,x6的平均数为1,方差为53.
(1)求x12+x22+⋯+x62的值;
(2)若在这组数据中加入另一个数据x7,重新计算,平均数无变化,求这7个数据的方差(结果用分数表示).
答案和解析
1.【答案】D
【解析】解:求30个数据的平均数时,错将其中一个数据75输入为15,即使总和减少了60,
那么由此求出的这组数据的平均数与实际平均数的差是−6030=−2;
故选:D.
利用平均数的定义可得.将其中一个数据75输入为15,也就是数据的和少了60,其平均数就少了60除以30,从而得出答案.
本题考查平均数的性质,求数据的平均值和方差是研究数据常做的,平均值反映数据的平均水平,而方差反映数据的波动大小,从两个方面可以准确的把握数据的情况.
2.【答案】B
【解析】解:该足球队队员的平均年龄是12×7+13×10+14×3+15×222=13(岁),
故选:B.
直接利用加权平均数的定义计算可得.
本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
3.【答案】C
【解析】解:∵数据a1,a2,a3,a4,a5的平均数为k1,
∴a1+a2+a3+a4+a5=5k1,
∵a6,a7,a8,a9,a10的平均数为k2,
∴a6+a7+a8+a9+a10=5k2,
∴a1+a2+a3+a4+a5+a6+a7+a8+a9+a10=5k1+5k2,
∴a1,a2,a3,…,a8,a9,a10的平均数为5k1+5k210=k1+k22=m,
∵k1与k2的平均数为k,
∴k=k1+k22,
∴k=m;
故选:C.
先分别求出数据a1,a2,a3,a4,a5和a6,a7,a8,a9,a10的和,根据平均数的计算公式求出a1,a2,a3,…,a8,a9,a10的平均数,再与a1,a2,a3,…,a8,a9,a10的平均数为m进行比较,即可得出答案.
此题考查了加权平均数,用到的知识点是加权平均数的计算公式,关键是根据加权平均数求出总数.
4.【答案】D
【解析】
【分析】
本题考查算术平均数,解题的关键是明确算术平均数的计算方法.根据题意可以得到求出的平均数与实际平均数之间的差值,本题得以解决.
【解答】
解:∵(105−15)÷30=90÷30=3,
∴求出的平均数与实际平均数的差是−3,
故选D.
5.【答案】A
【解析】解:∵4,4,6,6,8,a这组数据有唯一的众数,且4和6都出现两次
∴有a=4或a=6两种情况
当a=4时,这组数据为:4,4,4,6,6,8,中位数为:4+62=5 满足题意.
当a=6时,这组数据为:4,4,6,6,6,8,中位数为:6+62=6≠5,不满足题意,所以a=6舍去.
∴a=4,
故选A.
本题考查了众数和中位数,一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则最中间两个数据的平均数就是这组数据的中位数.
解答本题的关键是熟练掌握中位数和众数的定义.
6.【答案】C
【解析】解:(1)最高分是95分不是90分.
(2)根据众数、中位数的定义可知,众数是90,中位数也是90.
所以正确答案应选C.
故选:C.
认真阅读题意,分析折线图,运用中位数、众数定义来做即可.
考查折线统计图的认识,众数、中位数的定义,关键是对折线统计图的理解和众数、中位数定义的理解.
7.【答案】D
【解析】
【分析】
本题结合平均数考查了确定一组数据的中位数的能力.涉及到分类讨论思想,较难,要明确中位数的值与大小排列顺序有关,一些学生往往对这个概念掌握不清楚,计算方法不明确而解答不完整.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数,因为中位数的值与大小排列顺序有关,而此题中x的大小位置未定,故应该分类讨论x所处的所有位置情况:从小到大(或从大到小)排列在中间(在第二位或第三位结果不影响);结尾;开始的位置.
【解答】
解:(1)将这组数据从大到小的顺序排列后20,20,x,15,处于中间位置的那个数是20,x,
那么由中位数的定义可知,(20+x)÷2=(20+20+x+15)÷4,
x=15,符合题意;中位数为:(20+15)=17.5
(2)将这组数据从大到小的顺序排列后20,20,15,x,中位数是(20+15)÷2=17.5,
此时平均数是(20+20+x+15)÷4=17.5,
x=15,符合题意;
(3)将这组数据从大到小的顺序排列后x,20,20,15,中位数是20,
平均数(20+20+x+15)÷4=20,
x=25,符合题意;
所以中位数是20或17.5.
故选D.
8.【答案】C
【解析】
【分析】
本题考查的是众数,中位数有关知识,根据百分比,中位数,众数的定义对每个问题分别解答,即可确定选项.
【解答】
解:①28+8+44+20+24+8+4×100%=60%,正确,
②D等有4人,但看不出其具体的份数,错误,
③该班共有6人,在D等,C等的义工24人,所以中位数在第三组,正确,
④虽然第三组的人数多,但成绩分数不确定,所以众数不确定,错误.
故选C.
9.【答案】D
【解析】
【分析】
此题主要考查了平均数以及中位数和众数的定义求法和标准差的意义,正确把握相关定义是解题关键.分别利用平均数以及中位数和众数的定义求法和标准差的意义分别分析得出答案.
【解答】
解:平均数为:(13000+3300+6800+4500×2+3000+8000+2800×3)÷10=5150,
中位数是:(3300+4500)÷2=3900,
众数是:2800,
标准差反映的是数据的波动大小,无法反映这些员工月平均工资水平,只有中位数3900,能够较好反映这些员工月平均工资水平.
故选D.
10.【答案】D
【解析】
【分析】
此题考查了方差、平均数、中位数及众数的知识,属于基础题,掌握各部分的定义及计算方法是解题关键.
根据平均数的计算公式、中位数、众数的定义以及方差公式分别对每一项进行分析即可.
【解答】
解:平均数=(−1−3−1+5)÷4=0,
把这些数从小到大排列为:−3,−1,−1,5,
则中位数是−1;
∵数据−1出现两次最多,
∴众数为−1,
方差=14[(5−0)2+2(−1−0)2+(−3−0)2]=9.
故选:D.
11.【答案】D
【解析】
【分析】
此题考查了方差,若一组数据中的各个数据都加上或减去同一个数后得到的新数据的方差与原数据的方差相等;若一组数据中的各个数据都扩大或缩小几倍,则新数据的方差扩大或缩小其平方倍.根据方差的性质,即可计算出3x1,3x2,3x3,…,3xn的方差.
【解答】
解:∵x1,x2,x3,…,xn的方差为2,
又∵一组数据中的各个数据都扩大几倍,则新数据的方差扩大其平方倍,
∴3x1,3x2,3x3,…,3xn的方差为32×2=18,
故选D.
12.【答案】B
【解析】
【分析】
本题考查方差的定义.可以推广到一般的情况即样本中如果每个数据都加上一个数x,则平均值为x+x ,方差不变.如果样本中每个数据都乘以一个数n,这平均值为nx,方差为n2⋅S2.
显然本题样本中的每个数据都乘以3,则平均值为3x,代入方差公式可以求得本题的方差.
【解答】
解:由题意可知:
x1、x2、x3的方差S2=13x1−x2+x2−x2+x3−x2.
样本3x1、3x2、3x3平均值为3x,
则方差S22=133x1−3x2+3x2−3x2+3x3−3x2
=139x1−x2+9x2−x2+9x3−x2
=3x1−x2+x2−x2+x3−x2
=9S2.
故选:B.
13.【答案】−2
【解析】解:设报3的人心里想的数是x,
则报5的人心里想的数应是8−x,
于是报7的人心里想的数是12−(8−x)=4+x,
报9的人心里想的数是16−(4+x)=12−x,
报1的人心里想的数是20−(12−x)=8+x,
报3的人心里想的数是4−(8+x)=−4−x,
所以得x=−4−x,
解得x=−2.
故答案为:−2.
先设报3的人心里想的数,利用平均数的定义表示报5的人心里想的数;报7的人心里想的数;报9的人心里想的数;报1的人心里想的数,最后建立方程,解方程即可.
本题考查了一元一次方程的应用,解答此题的关键是列出方程.
14.【答案】15.3
【解析】解:该店当月销售出水果的平均价格是11×60%+18×15%+24×25%=15.3(元),
故答案为:15.3.
根据加权平均数的计算方法,分别用单价乘以相应的百分比,计算即可得解.
本题考查扇形统计图及加权平均数,解题的关键是掌握扇形统计图直接反映部分占总体的百分比大小及加权平均数的计算公式.
15.【答案】①④
【解析】
【分析】
本题考查了中位数、众数、平均数和极差的概念,根据中位数、众数、平均数和极差的概念分别进行解答,即可得出答案.
【解答】
解:∵共有40名同学,最中间的数是第20和21个数的平均数,
∴成绩的中位数在80≤x<90,
故①正确;
∵无法判断成绩的众数具体是多少,
∴成绩的众数无法判断,
故②不正确;
∵60≤x<70的人数只有4人,∴这40名同学的平均成绩不能为70,故③不正确;
成绩的极差可能为100−60=40,故④正确;
故答案为①④.
16.【答案】0.9
【解析】解:由方差的计算公式可得:
S2=1n[(x1−x−)2+(x2−x−)2+…+(xn−x−)2]
=1n[x12+x22+…+xn2+nx−2−2x−(x1+x2+…+xn)]
=1n[x12+x22+…+xn2+nx−2−2nx−2]=1n[x12+x22+…+xn2]−x−2=5640−12
=1.4−0.5
=0.9.
故填0.9.
根据方差的公式计算即可.方差S2=1n[(x1−x−)2+(x2−x−)2+…+(xn−x−)2].
本题考查方差的计算:一般地设n个数据,x1,x2,…xn的平均数为x−,则方差S2=1n[x12+x22+…+xn2]−x−2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
17.【答案】逐年增长
【解析】解:(1)根据图表可知我国教育经费投入呈现出趋势逐年增长趋势;
(2)根据图表我国教育经费平均数=(2949+3349+3849+4638+5480)÷5=4053亿元;
(3)设这两年的教育经费的平均增长率为x,
则5480(1+x)2=7891
解得x1≈0.20 x2≈−2.2(舍去)(结果精确到0.01)
∴x=0.20=20%.
故答案为(1)逐年增长;
(2)我国1998年~2002年教育经费的年平均数为4053亿元;
(3)教育经费平均增长率为20%.
(1)从图中可以我国从1998年~2002年每年教育经费投入一年比一年高,所以呈现逐年增长的趋势;
(2)我国从1998年~2002年每年教育经费投入分别是2949亿元,3349亿元,3849亿元,4638亿元,5480亿元,所以教育经费的年平均数为(2949+3349+3849+4638+5480)÷5=4053亿元;
(3)第三问考查数量平均变化率问题,解题的关键是正确列出一元二次方程.原来的数量为a,平均每次增长或降低的百分率为x的话,经过第一次调整,就调整到a×(1±x),再经过第二次调整就是a×(1±x)(1±x)=a(1±x)2.增长用“+”,下降用“−”.
本题主要考查的知识点:(1)平均数的求法;(2)涉及一元二次方程的平均变化率的求解.
18.【答案】解:(1)这个班级的学生人数为15÷30%=50(人),
选择C饮品的人数为50−(10+15+5)=20(人),
补全图形如下:
(2)10×0+15×2+20×3+5×450=2.2(元),
答:该班同学每天用于饮品的人均花费是2.2元;
(3)列表如下:
a
b
c
d
e
a
---
(b,a)
(c,a)
(d,a)
(e,a)
b
(a,b)
---
(c,b)
(d,b)
(e,b)
c
(a,c)
(b,c)
---
(d,c)
(e,c)
d
(a,d)
(b,d)
(c,d)
---
(e,d)
e
(a,e)
(b,e)
(c,e)
(d,e)
---
由列表知共有20种等可能结果,其中恰好抽到2名班长的有2种结果,
所以恰好抽到2名班长的概率为220=110.
【解析】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
(1)由B饮品的人数及其所占百分比可得总人数,再根据各饮品的人数之和等于总人数求出C的人数即可补全图形;
(2)根据加权平均数的定义计算可得;
(3)列表得出所有等可能结果,从中找到符合条件的结果,再根据概率公式计算可得.
19.【答案】解:(1)设1号电池每节重x克,5号电池每节重y克,
根据题意得4x+5y=4602x+3y=240
解之得x=90y=20.
(2)∵x−1号=29+30+32+28+315=30(节);x−5号=51+53+47+49+505=50(节)
∴总重量=(30×90+50×20)×30=111(千克).
答:(1)1号和5号电池每节分别重90克,20克;
(2)两种废电池的样本平均数分别为30节,50节.该月(30天)环保小组收集废电池的总重量是111千克.
【解析】根据题意列出方程组求出1号电池和5号电池的重量,然后再利用平均数求出电池的总重量.
解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.学会用样本估计总体的方法也是解决此题的关键.
20.【答案】D 12 10 C
【解析】解:(1)∵在样本中,男生共有2+4+8+12+14=40人,
∴中位数是第20和第21人的平均数,
∴男生身高的中位数落在D组,
女生身高在B组的人数有40×(1−35%−20%−15%−5%)=12人,
故答案为:D、12;
(2)在样本中,身高在170≤x<175之间的人数共有8+40×5%=10人,
∵A组人数为2+40×20%=10人,B组人数为4+12=16人,C组人数为12+40×35%=26人,D组人数为14+40×10%=18人,E组人数为8+40×5%=10人,
∴C组人数最多,
故答案为:10、C;
(3)500×12+1440+480×(35%+10%)=541(人),
故估计身高在160≤x<170之间的学生约有541人.
(1)先求出男生总人数,再根据中位数的定义解答即可,总女生总人数乘以B组的百分比可得;
(2)将位于这一小组内的频数相加,分别计算出各组人数之和即可求得结果;
(3)分别用男、女生的人数乘以对应的百分比,相加即可得解.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
21.【答案】解:(1)参加这次夏令营活动的初中生共有200×(1−10%−20%−30%)=80人;
(2)小学生、高中生和大学生的人数为200×20%=40,200×30%=60,200×10%=20,
所以平均每人捐款=40×5+80×10+60×15+20×20200=11.5(元);
(3)因为初中生最多,所以众数为10(元).
【解析】(1)参加这次夏令营活动的初中生所占比例是:1−10%−20%−30%=40%,就可以求出人数.
(2)小学生、高中生和大学生的人数为200×20%=40,200×30%=60,200×10%=20,根据平均数公式就可以求出平均数.
(3)因为初中生最多,所以众数为初中生捐款数.
本题为统计题,考查了扇形图、加权平均数和众数的含义.提高了学生的综合应用能力,解题时要细心.
22.【答案】解:(1)这15位学生周销售量的平均数=(450×1+130×1+60×3+50×5+40×3+35×2)÷15=80,
中位数为50,众数为50;
(2)不合理.因为15人中有13人销售量达不到80,周销售额定为50较合适,因为50是众数也是中位数.
【解析】(1)根据加权平均数的定义、中位数的定义和众数的定义求解;
(2)由于前面两人的周销售量与其他人相差太大,它们对平均数影响较大,这样用众数中位数50作为周销售定额比较合理.
此题考查了学生对中位数,众数,平均数的掌握情况.它们都是反映数据集中趋势的指标.
23.【答案】解:(1)甲段台阶高度的中位数是15,乙段台阶高度的众数是15;
(2)乙段台阶更方便游客行走,
因为甲路段台阶高度的平均数是15,
所以按每级台阶为15cm的高度进行整修.
【解析】(1)根据中位数和和众数的定义即可求解;
(2)由于要方便游客行走,要重新整修上山的小路,对于这两段台阶路,在台阶数不变的情况下,利用方差的定义即可解决问题.
此题主要考查了方差在实际生活中的应用,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
24.【答案】解:(1)数学平均分是:15×(71+72+…+70)=70分,
英语标准差为:15[(88−85)2+(82−85)2+(94−85)2+(85−85)2+(76−85)2=36=6;
(2)∵数学标准分=71−702=22,英语标准分=88−856=0.5,22>0.5,
∴数学更好.
【解析】(1)由平均数、标准差的公式进行计算即可;
(2)代入公式:标准分=(个人成绩−平均成绩)÷成绩标准差计算,再比较即可.
本题考查的是标准差的计算,计算标准差需要先算出方差,计算方差的步骤是:①计算数据的平均数x−;②计算偏差,即每个数据与平均数的差;③计算偏差的平方和;④偏差的平方和除以数据个数.标准差即方差的算术平方根;注意标准差和方差一样都是非负数.
25.【答案】解:(1)∵数据x1,x2,⋯,x6的平均数为1,
∴x1+x2+⋯+x6=1×6=6,
又∵方差为53,
∴s2=16[(x1−1)2+(x2−1)2+⋯+(x6−1)2]
=16[x12+x22+⋯+x62−2(x1+x2+⋯+x6)+6]
=16(x12+x22+⋯+x62−2×6+6)
=16(x12+x22+⋯+x62)−1=53,
∴x12+x22+⋯+x62=16.
(2)∵数据x1,x2,⋯,x7的平均数为1,
∴x1+x2+⋯+x7=1×7=7,
∵x1+x2+⋯+x6=6,
∴x7=1,
∵16[(x1−1)2+(x2−1)2+⋯+(x6−1)2]=53,
∴(x1−1)2+(x2−1)2+⋯+(x6−1)2=10,
∴s′2=17[(x1−1)2+(x2−1)2+⋯+(x7−1)2]
=17×[10+(1−1)2]
=107.
【解析】
【分析】本题考查了平均数与方差的意义.平均数是指在一组数据中所有数据之和再除以数据的个数.一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.计算公式是:s2=
1
n
[(x1−
x
)2+(x2−
x
)2+…+(xn−
x
)2].
(1)先由数据x1,x2,…x6的平均数为1,得出x1+x2+…+x6=1×6=6,再根据方差为
5
3
,得到S2=
1
6
[(x1−1)2+(x2−1)2+…+(x6−1)2]=
5
3
,利用完全平方公式求出
1
6
(x12+x22+…+x62−2×6+6)=
5
3
,进而求解即可;
(2)先由数据x1,x2,…x7的平均数为1,得出x1+x2+…+x7=1×7=7,而x1+x2+…+x6=6,所以x7=1;再根据
1
6
[(x1−1)2+(x2−1)2+…+(x6−1)2]=
5
3
,得出(x1−1)2+(x2−1)2+…+(x6−1)2=10,然后根据方差的计算公式即可求出这7个数据的方差.
相关资料
更多









