2022学年杭州市源清中学高一数学12月月考试卷

这是一份2022学年杭州市源清中学高一数学12月月考试卷，共7页。试卷主要包含了选择题，填空题，解做题，附加题等内容，欢迎下载使用。
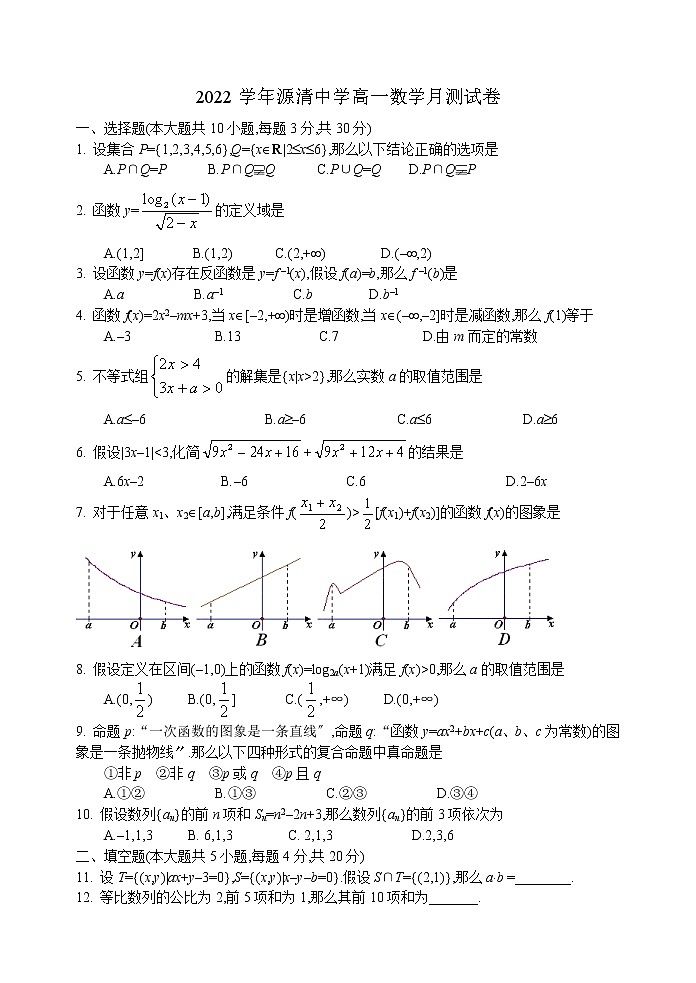
2022学年源清中学高一数学月测试卷一、选择题(本大题共10小题,每题3分,共30分)1. 设集合P={1,2,3,4,5,6},Q={xR|2x6},那么以下结论正确的选项是A.P∩Q=P　　　B.P∩QQ      C.P∪Q=Q　　D.P∩QP2. 函数y=的定义域是A.(1,2]       B.(1,2)      C.(2,+)        D.(–,2) 3. 设函数y=f(x)存在反函数是y=f –1(x),假设f(a)=b,那么f –1(b)是A.a　　　　　B.a–1　　　　　C.b　　　　D.b–14. 函数f(x)=2x2–mx+3,当x[–2,+)时是增函数,当x(–,–2]时是减函数,那么f(1)等于A.–3            B.13           C.7            D.由m而定的常数5. 不等式组的解集是{x|x>2},那么实数a的取值范围是A.a–6                 B.a–6             C.a6             D.a66. 假设|3x–1|<3,化简+的结果是A.6x–2       　　B.–6　　　　　　　C.6　　　　　　　　　　D.2–6x7. 对于任意x1、x2[a,b],满足条件f()>[f(x1)+f(x2)]的函数f(x)的图象是8. 假设定义在区间(–1,0)上的函数f(x)=log2a(x+1)满足f(x)>0,那么a的取值范围是A.(0,)  B.(0,]       C.(,+∞)  D.(0,+∞)9. 命题p:“一次函数的图象是一条直线〞,命题q:“函数y=ax2+bx+c(a、b、c为常数)的图象是一条抛物线〞.那么以下四种形式的复合命题中真命题是①非p　②非q　③p或q　④p且qA.①②  　　    B.①③ 　　     C.②③ 　　     D.③④10. 假设数列{an}的前n项和Sn=n2–2n+3,那么数列{an}的前3项依次为A.–1,1,3  B. 6,1,3        C. 2,1,3      D.2,3,6二、填空题(本大题共5小题,每题4分,共20分)11. 设T={(x,y)|ax+y–3=0},S={(x,y)|x–y–b=0}.假设S∩T={(2,1)},那么ab =________.12. 等比数列的公比为2,前5项和为1,那么其前10项和为_______.13. 1992年底世界人口到达54.8亿,假设人口的年平均增长率为1%,经过x年后世界人口数为 y亿,那么y与x的函数解析式为_________.14. a、b是两个命题,如果a是b的充分条件,那么a是b的_______条件.(填“充分条件〞、或“必要条件〞、或“充要条件〞)15. 假设函数y=ax与y= –在(0,+∞)上都是减函数,那么函数y=ax2+bx在(0,+∞)上是单调递_______函数.〔填“增函数〞或“减函数〞〕三、解做题(本大题共5小题,每题10分,共50分.解容许写出文字说明、证实过程或演算步骤)16. U=R,A={x||x–2|>1},B={x|0},求A∩B,A∪B,(∁UA)∪B. 17. 在逐项递增的等差数列｛an｝中,a1+a4+a7=15,a2a4a6=45,求其通项an. 18. 函数.(Ⅰ)画出函数的简图；(Ⅱ)求该函数的值域〔仅由图象指出其值域得2分〕. 19. 某摩托车生产企业,上年度生产摩托车的投入本钱为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆. 本年度为适应市场需求,方案提升产品档次,适当增加投入本钱. 假设每辆车投入本钱增加的比例为x(0<x<1),那么出厂价相应的提升比例为0.75x,同时预计年销售量增加的比例为0.6x.(Ⅰ)写出本年度预计的年利润y与投入增加的比例x的关系式;(Ⅱ)为使本年度的年利润比上年有所增加,问投入本钱增加的比例x应在什么范围内. 20. f(x)=log4(2x+3–x2).(Ⅰ)求f(x)定义域；(Ⅱ)求f(x)的单调区间；(Ⅲ)求f(x)的最大值,并求取最大值时x的值. 四、附加题(本大题共2小题,每题10分,共20分)21. a<0,设p:实数x满足x2–4ax+3a2<0；q:实数x满足x2–x–60或x2+2x–8>0. 假设p是q的必要不充分条件,求a的取值范围. 22. 假设关于x的方程4x+(a+3)2x+5=0至少有一个实根在区间[1,2]内,求实数a的取值范围.
2022学年源清中学高一数学月测试卷答卷 一、选择题(本大题共10小题,每题3分,共30分) 题号12345678910答案           二、填空题(本大题共5小题,每题4分,共20分) 11._________;12.______________;13.________________;14.__________;15.____________ 三、解做题(本大题共5小题,每题10分,共50分)16. U=R,A={x||x–2|>1},B={x|0},求A∩B,A∪B,(∁UA)∪B.            17. 在逐项递增的等差数列｛an｝中,a1+a4+a7=15,a2a4a6=45,求其通项an.  
18. 函数.(Ⅰ)画出函数的简图；(Ⅱ)求该函数的值域〔仅由图象指出其值域得2分〕.             19. 某摩托车生产企业,上年度生产摩托车的投入本钱为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆. 本年度为适应市场需求,方案提升产品档次,适当增加投入本钱. 假设每辆车投入本钱增加的比例为x(0<x<1),那么出厂价相应的提升比例为0.75x,同时预计年销售量增加的比例为0.6x.(Ⅰ)写出本年度预计的年利润y与投入增加的比例x的关系式;(Ⅱ)为使本年度的年利润比上年有所增加,问投入本钱增加的比例x应在什么范围内. 
20. f(x)=log4(2x+3–x2).(Ⅰ)求f(x)定义域；(Ⅱ)求f(x)的单调区间；(Ⅲ)求f(x)的最大值,并求取最大值时x的值.                四、附加题(本大题共2小题,每题10分,共20分)21. a<0,设p:实数x满足x2–4ax+3a2<0；q:实数x满足x2–x–60或x2+2x–8>0. 假设p是q的必要不充分条件,求a的取值范围. 
22. 假设关于x的方程4x+(a+3)2x+5=0至少有一个实根在区间[1,2]内,求实数a的取值范围.
参考答案：题号12345678910答案DBABBCDACC11. 1         12. 33           13. y=54.81.01x   14. 必要条件  15. 减函数16. A∩B={x|x<1或x>3},A∪B={x|x1或x>2},(∁UA)∪B=R17.an=2n–318.(0,1]19.(1)y=–60x2+20x+200(2)0<x<20.(1)(–1,3)  (2) f(x)的减区间是(1,3),增区间是(–1,1)  (3)当x=1时,f(x)取最大值1.21.a–4或a<022.