6.2 方程的简单变形 华师版七年级数学下册原创新授课件

这是一份6.2 方程的简单变形 华师版七年级数学下册原创新授课件，共15页。
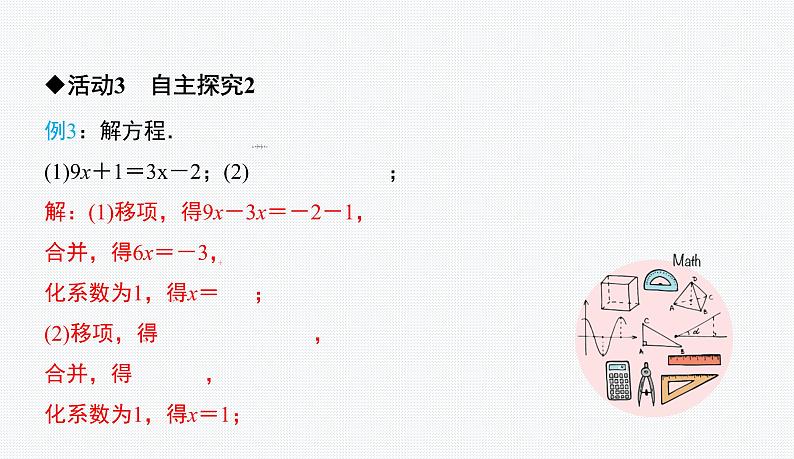
第六章　一元一次方程课题　方程的简单变形一、学习目标二、学习重难点1．运用方程的变形规律熟练解方程．2．理解解方程的步骤，掌握移项变号规则．通过解方程过程的探讨，使学生学会解方程的步骤．理解解方程的步骤，掌握移项变号规则． 活动1 旧知回顾三、情境导入1．等式的基本性质是什么？用字母怎么表示．答：等式的基本性质1：等式两边都加上(或都减去)同一个数或同一个整式，所得的结果仍是等式．等式的基本性质2：等式两边都乘以(或都除以)同一个数(除数不能为0)，所得的结果仍是等式．2．用等式的基本性质解方程：2a＋3＝a＋1.解：等式的两边都加上－a－3，得a＝－2.如果a＝b，那么ac＝bc， ＝ (c≠0)．如果a＝b，那么a＋c＝b＋c，a－c＝b－c. 活动1 自主探究1四、自学互研1．由等式的性质可以得到方程变形的规则：2．移项：3．将未知数的系数化为1：4．解方程的过程，都是将方程进行适当的变形，得到x＝a的形式．将方程中的某些项改变符号后，从方程的一边移到另一边，像这样的形叫做移项．将方程的两边都除以未知数的系数，这样的变形叫做将未知数的系数化为1.(1)方程两边都加上(或都减去)同一个数或同一个整式，方程的解不变；(2)方程两边都乘以(或都除以)同一个不等于0的数，方程的解不变． 活动2 合作探究1例1：下列变形中属于移项的是 (　　)A．由3x＝1得x＝ B．由 ＝2得x＝4C．由2x＋1＝0得2x＝－1 D．由3x－2＝0得2－3x＝0分析：注意移项的定义：从一边移到另一边，必须变号．而不是简单的变形．C例2：解方程．(1)x－1＝2 016；(2)5x＝4x－2；(3) ；(4)0.5x＝x－1.解：(1)移项，得x＝2 016＋1，∴x＝2 017；(2)移项，得5x－4x＝－2，∴x＝－2；(3)系数化为1，得 ，∴x＝ ；(4)移项，得0.5x－x＝－1，∴－0.5x＝－1，∴化系数为1，得x＝2.活动3 自主探究2例3：解方程． (1)9x＋1＝3x－2；(2) ；解：(1)移项，得9x－3x＝－2－1，合并，得6x＝－3，化系数为1，得x＝ ；(2)移项，得 ，合并，得 ，化系数为1，得x＝1；(3)2.4x＋2.4－1.4x＝3x；解：移项，得2.4x－1.4x－3x＝－2.4，合并，得－2x＝－2.4，化系数为1，得x＝1.2.典例1 ：解下列方程：（1）x－5＝7；（2）4x＝3x－4.解（1）两边都加上5，得x＝7＋5，即x＝12.(2)两边都减去3x，得4x－3x＝-4，即x＝-4.典例2 ：解下列方程：(2)方程两边都除以 （或都乘以 ），得即（1）-5x=2；（2） x=解（1）方程两边否除以-5，得x= -x＝x＝ ÷ ＝ ×活动4 合作探究2例4：解方程：3x－3＝2x－3.小明同学是这样解的：方程两边都加上3，得3x＝2x，方程两边都除以x，得3＝2，所以此方程无解．小明同学的解答是否正确？说明理由．解：不正确．将原方程变形为3x＝2x后，方程两边不能都除以x，还应再移项，得x＝0.所以方程的解是x＝0.练 习解下列方程:44 x+64=328解:44 x=328-6444 x=26444 x 264=4444x=6.由44 x+64=328移项，得即两边都除以44，得 活动5完成《名师测控》手册《精英新课堂》手册 （1）一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项. （2）移项的依据是等式的性质1.1.移项2.解形如“a x+b=c x + d”的方程的一般步骤：(1)移项；(2)合并同类项；(3)化未知数的系数为1. 活动6 课堂小结五、作业布置与教学反思1．作业布置 对应课时练习．2．教学反思