2023高考数学二轮复习专题33 直线的方程（解析版）

这是一份2023高考数学二轮复习专题33 直线的方程（解析版），共45页。

专题33 直线的方程
【考点预测】
知识点一：直线的倾斜角和斜率
1．直线的倾斜角
若直线与轴相交，则以轴正方向为始边，绕交点逆时针旋转直至与重合所成的角称为直线的倾斜角，通常用表示
（1）若直线与轴平行（或重合），则倾斜角为
（2）倾斜角的取值范围
2．直线的斜率
设直线的倾斜角为，则的正切值称为直线的斜率，记为
（1）当时，斜率不存在；所以竖直线是不存在斜率的
（2）所有的直线均有倾斜角，但是不是所有的直线均有斜率
（3）斜率与倾斜角都是刻画直线的倾斜程度，但就其应用范围，斜率适用的范围更广（与直线方程相联系）
（4）越大，直线越陡峭
（5）倾斜角与斜率的关系

当时，直线平行于轴或与轴重合；
当时，直线的倾斜角为锐角，倾斜角随的增大而增大；
当时，直线的倾斜角为钝角，倾斜角随的增大而减小；
3．过两点的直线斜率公式
已知直线上任意两点，，则
（1）直线的斜率是确定的，与所取的点无关．
（2）若，则直线的斜率不存在，此时直线的倾斜角为90°
4．三点共线．
两直线的斜率相等→三点共线；反过来，三点共线，则直线的斜率相等（斜率存在时）或斜率都不存在．
知识点二：直线的方程
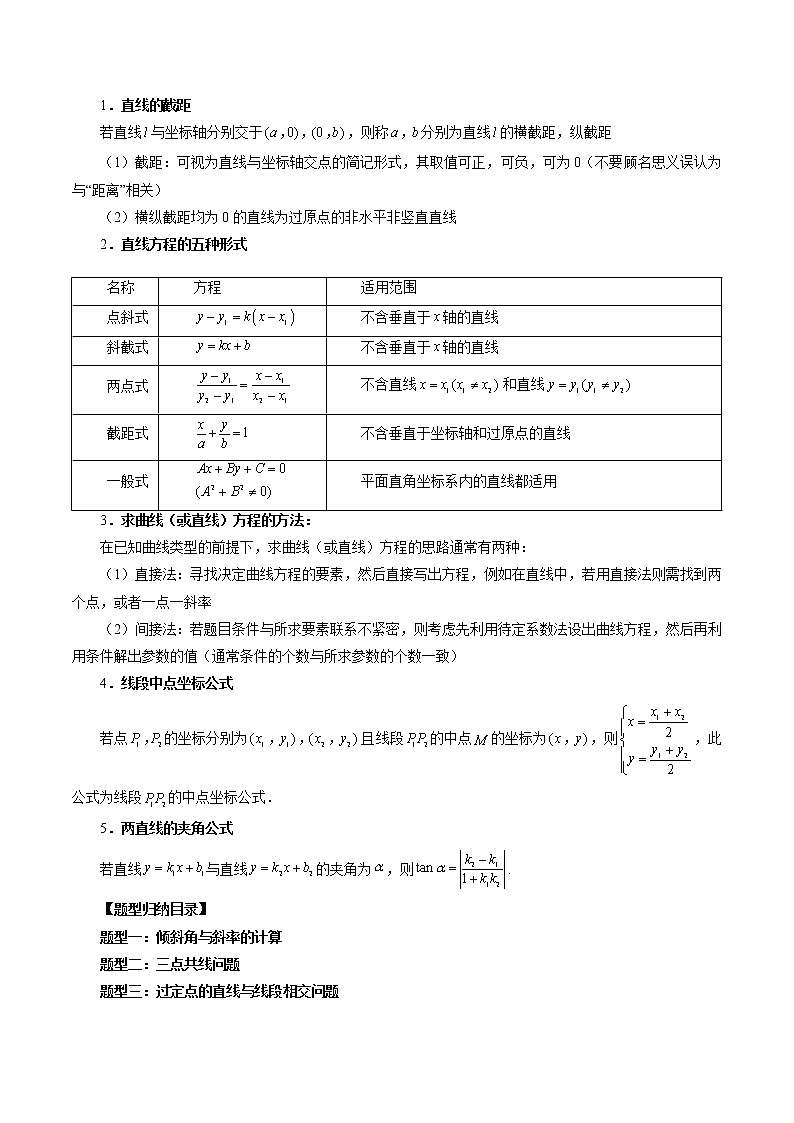
1．直线的截距
若直线与坐标轴分别交于，则称分别为直线的横截距，纵截距
（1）截距：可视为直线与坐标轴交点的简记形式，其取值可正，可负，可为0（不要顾名思义误认为与“距离”相关）
（2）横纵截距均为0的直线为过原点的非水平非竖直直线
2．直线方程的五种形式
名称
方程
适用范围
点斜式

不含垂直于轴的直线
斜截式

不含垂直于轴的直线
两点式

不含直线和直线
截距式

不含垂直于坐标轴和过原点的直线
一般式

平面直角坐标系内的直线都适用
3．求曲线（或直线）方程的方法：
在已知曲线类型的前提下，求曲线（或直线）方程的思路通常有两种：
（1）直接法：寻找决定曲线方程的要素，然后直接写出方程，例如在直线中，若用直接法则需找到两个点，或者一点一斜率
（2）间接法：若题目条件与所求要素联系不紧密，则考虑先利用待定系数法设出曲线方程，然后再利用条件解出参数的值（通常条件的个数与所求参数的个数一致）
4．线段中点坐标公式
若点的坐标分别为且线段的中点的坐标为，则，此公式为线段的中点坐标公式．
5．两直线的夹角公式
若直线与直线的夹角为，则.
【题型归纳目录】
题型一：倾斜角与斜率的计算
题型二：三点共线问题
题型三：过定点的直线与线段相交问题
题型四：直线的方程
题型五：直线与坐标轴围成的三角形问题
题型六：两直线的夹角问题
题型七：直线过定点问题
题型八：轨迹方程
题型九：中点公式

【典例例题】
题型一：倾斜角与斜率的计算
例1．（2022·全国·高三专题练习）求经过（其中）、两点的直线的倾斜角的取值范围．
【解析】由题意，当时，倾斜角，
当时，，即倾斜角为锐角；
综上得：．
例2．（2022·全国·高三专题练习）过点的直线的倾斜角为（       ）
A． B． C．1 D．
【答案】A
【解析】过A、B的斜率为，则该直线的倾斜角为，
故选：A．
例3．（2022·全国·高三专题练习）若，且为第二象限角，则角的终边落在直线（       ）上.
A． B． C． D．
【答案】B
【解析】由为第二象限角可得，则，
则角的终边落在直线即上.
故选：B.
例4．（2022·全国·高三专题练习）如图，设直线，，的斜率分别为，，，则，，的大小关系为（       ）

A． B．
C． D．
【答案】A
【解析】由斜率的定义可知，.
故选：A．
例5．（2022·全国·高三专题练习）若一次函数所表示直线的倾斜角为，则的值为（       ）．
A． B． C． D．
【答案】D
【解析】的斜率为即

故选：D．
例6．（2022·全国·高三专题练习）设直线的斜率为，且，则直线的倾斜角的取值范围是（       ）
A． B．
C． D．
【答案】A
【解析】因为直线的斜率为，且，
，因为，
.
故选：A.
例7．（2022·全国·高三专题练习）已知直线的方程为，则直线
的倾斜角范围是（       ）
A． B．
C． D．
【答案】B
【解析】由直线的方程为，
所以，
即直线的斜率，由.
所以 ，又直线的倾斜角的取值范围为，
由正切函数的性质可得：直线的倾斜角为.
故选：B
例8．（2022·全国·高三专题练习）设直线的方程是倾斜角为.若，则的取值范围是（       ）
A． B．
C． D．
【答案】B
【解析】直线的方程是倾斜角为，
当时，直线的斜率不存在，则；
当时，.
若，则，求得；
若，则，求得.
综上可得，的取值范围为.
故选：B.
例9．（多选题）（2022·全国·高三专题练习）下列四个命题中，错误的有（       ）
A．若直线的倾斜角为，则
B．直线的倾斜角的取值范围为
C．若一条直线的倾斜角为，则此直线的斜率为
D．若一条直线的斜率为，则此直线的倾斜角为
【答案】ACD
【解析】因为直线的倾斜角的取值范围是，即，所以，
当时直线的斜率，故A、C均错误；B正确；
对于D：若直线的斜率，此时直线的倾斜角为，故D错误；
故选：ACD
例10．（2022·全国·高三专题练习）已知直线l经过点，两点，则直线l的斜率为______；若，则直线l的倾斜角的取值范围为______．
【答案】          或.
【解析】由题易知直线l的斜率存在，故.
则，当且仅当，即时，等号成立.
所以或，即直线l的倾斜角的取值范围是或.
故答案为：；或.
例11．（2022·全国·高三专题练习）若直线的倾斜角为α，则sin2α的值为___________.
【答案】
【解析】由题可知，，
则.
故答案为：.
【方法技巧与总结】
正确理解倾斜角的定义，明确倾斜角的取值范围，熟记斜率公式，根据该公式求出经过两点的直线斜率，当时，直线的斜率不存在，倾斜角为，求斜率可用，其中
为倾斜角，由此可见倾斜角与斜率相互关联，不可分割．牢记“斜率变化分两段，是其分界，遇到斜率要谨记，存在与否要讨论”．这可通过画正切函数在上的图像来认识．
题型二：三点共线问题
例12．（2022·全国·高三专题练习）若三点共线，则a的值为_________．
【答案】
【解析】由三点共线
故

故答案为：.
例13．（2022·全国·高三专题练习）若，，三点共线，则（       ）
A． B． C． D．
【答案】A
【解析】由于、、三点共线，
则，即，解得.
故选：A.
例14．（2022·北京·高三期末）已知、、三点共线，则的值为（       ）
A． B． C． D．
【答案】C
【解析】
利用可得出关于的等式，由此可求得实数的值.
【详解】
由于、、三点共线，则，即，解得.
故选：C.
【方法技巧与总结】
斜率是反映直线相对于轴正方向的倾斜程度的，直线上任意两点所确定的方向不变，即在同一直线上任意不同的两点所确定的斜率相等．这正是利用斜率可证三点共线的原因．
题型三：过定点的直线与线段相交问题
例15．（2022·全国·高三专题练习）经过点作直线l，且直线l与连接点，
的线段总有公共点，求直线l的倾斜角和斜率k的取值范围．
【解析】因为，，由与线段相交，

所以，
所以或，
由于在及均为增函数，
所以直线的倾斜角的范围为：.
故倾斜角的范围为，斜率k的范围是.
例16．（2022·全国·高三专题练习）已知直线：，点，，若直线与线段相交，则的取值范围为（       ）
A． B． C． D．
【答案】C
【解析】直线方程变形得：.
由得，∴直线恒过点，
，，
由图可知直线的斜率的取值范围为：或，
又，
∴或，即或，
又时直线的方程为，仍与线段相交，
∴的取值范围为.
故选：C.

例17．（2022·陕西·西安中学高三阶段练习（理））已知点在直线上，且满足，则的取值范围为_______．
【答案】
【解析】如图，作出直线及，它们的交点为，
直线上满足的点在点右下方，
，又直线的斜率为，，
由图可得的范围是．
故答案为：．

例18．（2022·全国·高三专题练习）已知，，点是线段（包括端点）上的动点，则的取值范围是 ________．
【答案】[1，2]
【解析】设，则可以看成过点与坐标原点的直线的斜率.
当点在线段上由点运动到点时，直线的斜率由增大到，如图所示.

又，，所以，即的取值范围是[1，2].
故答案为：[1，2]
例19．（2022·全国·高三专题练习）点在函数的图象上，当时，的取值范围是（       ）
A． B．
C． D．
【答案】B
【解析】因为点在函数的图象上，
所以时， ；当时，；
故设
而可看作函数的图象上的点与点 （-1，-2）连线的斜率，
故时，,
而 ,所以
故选：B.
例20．（2022·全国·高三专题练习）已知两点，，直线过点且与线段相交，则直线的斜率的取值范围是（       ）
A． B．或 C． D．
【答案】B
【解析】如下图示，

当直线过A时，，
当直线过B时，，
由图知：或.
故选：B
【方法技巧与总结】
一般地，若已知，过点作垂直于轴的直线，过点的任一直线的斜率为，则当与线段不相交时，夹在与之间；当与线段相交时，在与的两边．
题型四：直线的方程
例21．（2022·全国·高三专题练习）下列四个命题中真命题有_________个．
①经过定点的直线都可以用方程表示；
②经过任意两点的直线都可以用方程表示；
③不经过原点的直线都可以用方程表示；
④经过定点的直线都可以用方程表示．
【答案】1
【解析】①由于直线过定点，当直线斜率存在时，可用方程表示，
当直线斜率不存在时，方程是，①不正确；
②当时，经过任意两个不同的点的直线方程是，满足方程，
当时，经过任意两个不同的点的直线的斜率是，
则直线方程是，整理得，②正确；
③当直线斜率不存在时，不经过原点的直线方程是，不可以用方程表示，
当直线的斜率存在时，不经过原点的直线可以用方程表示，③不正确；
④当直线斜率不存在时，经过点的直线方程是，不可以用方程表示，
当直线的斜率存在时，经过点的直线可以用方程表示，④不正确，
所以给定的4个命题中，真命题只有1个.
故答案为：1
例22．（2022·全国·高三专题练习）设直线l过点，在两坐标轴上的截距的绝对值相等，则满足题设的直线l的条数为______条．
【答案】3
【解析】当坐标轴截距为0时，设方程为，
将代入得：，所以方程为；
当坐标轴截距不为0时，设方程为，
则有，解得：，或，
从而方程为或
所以满足题设的直线l的条数为3条.
故答案为：3
例23．（2022·全国·高三专题练习）已知直线的倾斜角为，且经过点，则直线的方程为（       ）
A． B． C． D．
【答案】C
【解析】由题意知：直线的斜率为，则直线的方程为.
故选：C.
例24．（2022·全国·高三专题练习）过两点和的直线在y轴上的截距为（       ）
A． B． C． D．
【答案】C
【解析】由题可知直线方程为：，即，
令x=0，则，故直线在y轴上的截距为.
故选：C.
例25．（2022·全国·高三专题练习）已知直线过点，，则直线的方程为（       ）
A． B． C． D．
【答案】C
【解析】由直线的两点式方程可得，
直线l的方程为，即．
故选：C．
例26．（2022·江苏·高三专题练习）已知直线和直线都过点，则过点和点的直线方程是（       ）
A． B． C． D．
【答案】A
【解析】把坐标代入两条直线和,得
,,
,
过点,的直线的方程是：,
,则,
,,
所求直线方程为：．
故选 ：A.
例27．（2022·全国·高三专题练习）已知直线在两坐标轴上的截距相等，则实数（       ）
A．1 B． C．或1 D．2或1
【答案】D
【解析】当时，直线，此时不符合题意，应舍去；
当时，直线，在轴与轴上的截距均为0，符合题意；
当且，由直线可得：横截距为，纵截距为.
由，解得：.
故的值是2或1.
故选：D
例28．（2022·全国·高三专题练习）过点且与两坐标轴上的截距相等的直线共有（       ）
A．1条 B．2条 C．3条 D．4条
【答案】B
【解析】①当直线的两坐标轴上的截距为0时，设直线方程为，由题意有，则，∴直线方程为满足条件；
②当直线的两坐标轴上的截距不为0时，设的方程为．把点代入直线方程得．解得，从而直线方程为.
故满足条件的直线方程为和．
故选：B．
例29．（2022·北京西城·高三阶段练习（理））已知直线不通过第一象限，则实数的取值范围__________．
【答案】
【解析】
由题意得直线恒过定点，且斜率为，
∵直线不通过第一象限，
∴，解得，
故实数的取值范围是．
答案：
例30．（2022·全国·高三专题练习）若直线l的方程中，，，则此直线必不经过（       ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
【答案】C
【解析】由，，，
知直线斜率，在轴上截距为，
所以此直线必不经过第三象限.
故选：C
例31．（2022·福建·莆田二中高三开学考试）直线经过第一、二、四象限，则（       ）
A．， B．，
C．， D．，
【答案】C
【解析】因为直线经过第一、二、四象限，则该直线的斜率，可得，
该直线在轴上的截距，可得.
故选：C.
例32．（多选题）（2022·全国·高三专题练习）过点且在两坐标轴上截距相等的直线方程为（       ）
A． B． C． D．
【答案】AC
【解析】当截距为0时，过点和原点，直线方程为，即，
当截距不为0时，设直线方程为，可得，
∴，所以直线方程为,
故选：AC.
例33．（多选题）（2022·全国·高三专题练习）过点，并且在两轴上的截距互为相反数的直线方程为（       ）
A． B．
C． D．
【答案】AB
【解析】若直线过原点，则直线的方程为，
将点代入得，所以直线方程为，即；
若直线不过原点，根据题意，设直线方程为，
将点代入得，故直线的方程为；
所以直线的方程为：或．
故选：AB．
例34．（2022·全国·高三专题练习）已知直线的倾斜角为，且在轴上的截距为，则直线的方程为（　　）
A． B．
C． D．
【答案】C
【解析】因为直线的倾斜角为，所以直线的斜率，
又直线在轴上的截距为，所以直线的方程为；
故选：C
【方法技巧与总结】
要重点掌握直线方程的特征值（主要指斜率、截距）等问题；熟练地掌握和应用直线方程的几种形式，尤其是点斜式、斜截式和一般式．
题型五：直线与坐标轴围成的三角形问题
例35．（2022·江苏·高三专题练习）在平面直角坐标系中，直线与坐标轴分别交于点，，则下列选项中错误的是（       ）
A．存在正实数使得△面积为的直线l恰有一条
B．存在正实数使得△面积为的直线l恰有二条
C．存在正实数使得△面积为的直线l恰有三条
D．存在正实数使得△面积为的直线l恰有四条
【答案】A
【解析】由题意，直线与轴、轴交点分别为，，
∴，作出其图象如图所示，


由图知，当时，有两解；当时，有三解；当时，有四解.
故选：A
例36．（2022·全国·高三专题练习）已知过定点直线在两坐标轴上的截距都是正值，且截距之和最小，则直线的方程为（       ）
A． B． C． D．
【答案】C
【解析】直线可变为，所以过定点，又因为直线在两坐标轴上的截距都是正值，可知，
令，所以直线与轴的交点为，
令，所以直线与轴的交点为，
所以，
当且仅当即时取等，所以此时直线为：.
故选：C.
例37．（2022·全国·高三专题练习）已知直线l经过点P(4，3)，且与x轴正半轴交于点A，与y轴正半轴交于点B，O为坐标原点.
（1）若点O到直线l的距离为4，求直线l的方程；
（2）求△OAB面积的最小值.
【解析】】（1）由题意可设直线的方程为，即，
则，解得．
故直线的方程为，即；
（2）直线的方程为，
，，依题意，解得，
则的面积为．
则（当且仅当时，等号成立）．
故面积的最小值为．
例38．（2022·江苏·高二专题练习）已知点、，设过点的直线l与的边AB交于点M（其中点M异于A、B两点），与边OB交于N（其中点N异于O、B两点），若设直线l的斜率为k．
(1)试用k来表示点M和N的坐标；
(2)求的面积S关于直线l的斜率k的函数关系式；
(3)当k为何值时，S取得最大值？并求此最大值．
【解析】(1)由已知得直线l斜率存在，设．
由，得；又，所以.
由，得．
(2).
(3)设，则．
，
当且仅当时，等号成立．
例39．（2022·湖北孝感·高二期中）已知直线的方程为点的坐标为.
(1)证明：直线一定经过第一象限；
(2)设直线与轴､轴分别交于，两点，当点到直线的距离取得最大值时，求的面积.
【解析】(1)直线：，整理可得：，
∴直线恒过和的交点，即直线恒过定点在第一象限，
∴直线一定经过第一象限；
(2)由（1）可得：直线恒过定点，
当与垂直时，到直线的距离最大，为，
又，故直线的斜率为，即，可得，
直线的方程为：，
令得：；令得：，即，，
∴，
∴.
例40．（2022·全国·高二专题练习）设直线的方程为．
(1)若在两坐标轴上的截距相等，求的一般式方程；
(2)若与轴正半轴的交点为，与轴负半轴的交点为，求为坐标原点）面积的最小值．
【解析】(1)对于直线的方程为，
当直线经过原点时，，求得，此时它的方程为；
当直线不经过原点时，它的方程即，由于它两坐标轴上的截距相等，
故有，求得，它的方程为，
综上可得，的一般式方程为，或．
(2)因为，令，则，令，则，所以，，
与轴正半轴的交点为，与轴负半轴的交点为，
的横坐标，的纵坐标，求得．
所以
，当且仅当时取等号，
故为坐标原点）面积的最小值为6．
例41．（2022·江苏·高二专题练习）直线，相交于点，其中.
（1）求证：、分别过定点、，并求点、的坐标；
（2）求的面积；
（3）问为何值时，最大？
【解析】（1）在直线的方程中令可得，则直线过定点，
在直线的方程中令可得，则直线过定点；
（2）联立直线、的方程，解得，即点.
，
，
，所以，；
（3）且，因此，当时，取得最大值，即.
例42．（2022·江苏·苏州中学高二期中）已知，为实数，过原点分别作直线，的垂线，垂足分别为， .
（1）若，且直线与轴、轴交于,两点，当面积最小时，求实数的值；
（2）若直线过点，设直线与的交点为，求证：点在一条直线上.
【解析】（1）
直线，
令，
令，
，
，
当时，，
面积最小时，实数的值为；
（2）原点的直线距离为，
同理原点的直线距离为，所以为圆的切线，
为切点，直线过点，且直线与相交于，
不在轴上，设，
所以直线化为，整理得，
同理方程为，设与的交点为，
所以有，
所以直线方程为，且过点，
，即点在直线上.
例43．（2022·江苏·高二课时练习）过点作直线l分别与x，y轴正半轴交于点A，B.
(1)若是等腰直角三角形，求直线l的方程；
(2)对于①最小，②面积最小，若选择___________作为条件，求直线l的方程.
【解析】(1)因为过点作直线l分别与x，y轴正半轴交于点A、B，且是等腰直角三角形，
所以直线l的倾斜角为，
所以直线l的斜率为，
所以直线l的方程为，即；
(2)设，，直线l的方程为，代入点可得，
若选①：，当且仅当时等号成立，
此时直线l的斜率，
所以直线l的方程为，即；
若选②：由，可得，当且仅当时等号成立，
所以，即面积最小为4，
此时直线l的斜率，
所以直线l的方程为，即.
例44．（2022·安徽省亳州市第一中学高二阶段练习）已知直线过点.
(1)若直线在两坐标轴上的截距相等，求直线的方程；
(2)若直线与x，y轴分别交于A，B两点且斜率为负，O为坐标原点，求的最小值.
【解析】(1)当直线过原点时，
则直线的方程为在两坐标轴上的截距相等；
当直线不过原点时，设直线l的方程为，
将点代入得，解得，
所以直线的方程为，
综上所述直线的方程为或；
(2)设直线的方程为，
当时，，
当时，，
故，
当且仅当，即时取等号，
所以的最小值为.
例45．（2022·全国·高二）过点作直线分别交轴、轴的正半轴于，两点．
(1)当取最小值时，求出最小值及直线的截距式方程；
(2)当取最小值时，求出最小值及直线的截距式方程．
【解析】(1)根据题意可设直线l的方程为,则,
直线l过点,,
又(当且仅当,即时取等号),
,即,
的最小值为8,此时直线l的截距式方程为.
(2)由（1）可知,,则,



(当且仅当,即时取等号).
的最小值为4,此时直线l的截距式方程为.
例46．（2022·浙江·绍兴一中高二期中）如图，过点的直线l交x轴，y轴正半轴于A､B两点，求使：

(1)面积最小时l的方程；
(2)最小时l的方程.
【解析】(1)设直线的方程为，
直线过点，
．
，
．．
当且仅当，即，时，取最小值4，
此时直线的方程为，即．
(2)由，得，
变形得，

．
当且仅当，，即，时，取最小值4．
此时直线的方程为．
例47．（2022·黑龙江·哈尔滨市第六中学校高二期中）直线l过点，且分别与轴正半轴交于、B两点，O为原点.
(1)当面积最小时，求直线l的方程；
(2)求的最小值及此时直线l的方程.
【解析】(1)设直线，且
∵直线过点
则
当且仅当即时取等号
所以的最小值为，
直线1即.
(2)由
∴，
当且仅当即时取等号，
∴此时直线,
故的最小值为9，此时直线l的方程.
例48．（2022·江苏省苏州第十中学校高二阶段练习）已知直线：．
（1）求经过的定点坐标；
（2）若直线交轴负半轴于点，交轴正半轴于点．
①的面积为，求的最小值和此时直线的方程；
②当取最小值时，求直线的方程．
【解析】（1）由可得：，
由可得，所以经过的定点坐标；
（2）直线：，
令可得；令，可得，
所以，
由可得：，
①的面积
，
当且仅当即时等号成立，的最小值为，
此时直线的方程为：即；
②设直线的倾斜角为，则，可得，，
所以，
令，
因为，可得，，
，
将两边平方可得：，
所以，
所以，
因为在上单调递增，所以
，所以，此时，
可得，所以，
所以直线的方程为.
【方法技巧与总结】
（1）由于已知直线的倾斜角（与斜率有关）及直线与坐标轴围成的三角形的面积（与截距有关），因而可选择斜截式直线方程，也可选用截距式直线方程，故有“题目决定解法”之说．
（2）在求直线方程时，要恰当地选择方程的形式，每种形式都具有特定的结论，所以根据已知条件恰当地选择方程的类型往往有助于问题的解决．例如：已知一点的坐标，求过这点的直线方程，通常选用点斜式，再由其他条件确定该直线在y轴上的截距；已知截距或两点，选择截距式或两点式．在求直线方程的过程中，确定的类型后，一般采用待定系数法求解，但要注意对特殊情况的讨论，以免遗漏．
题型六：两直线的夹角问题
例49．（2022·全国·高三专题练习）直线与的夹角为________．
【答案】
【解析】直线的斜率，即倾斜角满足，
直线的斜率，即倾斜角满足，
所以，
所以，
又两直线夹角的范围为，
所以两直线夹角为，
故答案为：.
例50．（2022·全国·高三专题练习）已知等腰三角形两腰所在直线的方程分别为与，原点在等腰三角形的底边上，则底边所在直线的斜率为___________.
【答案】3
【解析】直线的斜率，直线的斜率，
设底边所在直线为，
由题意，与的夹角等于与的夹角，
于是有，即，
化简得，解得或，
因为原点在等腰三角形的底边上，所以.
故答案为：3.
例51．（2022·上海·高三专题练习）两条直线，的夹角平分线所在直线的方程是________．
【答案】
【解析】因为直线的倾斜角为，的倾斜角为，且
由解得两直线的交点坐标为，所以可设两直线夹角平分线所在直线的方程为：．
∴，解得，即两直线夹角平分线所在直线的方程为：．
故答案为：．
例52．（2022·全国·高三专题练习）已知直线，，若直线l过且与直线m､n在第一象限围成一个等腰锐角三角形，则直线l的斜率是（       ）
A． B． C． D．2
【答案】A
【解析】根据题意，设直线的斜率为，
直线，，两直线相交于点，设，
点在直线上，直线与直线相交于点，
为等腰锐角三角形，
则，则，
故必为顶点，必有
则有，
必有，解可得：或，
则，
故选：．

例53．（2022·全国·高三专题练习（文））若等腰直角三角形一条直角边所在直线的斜率为，则斜边所在直线的斜率为（       ）
A．或2 B．或3 C．或4 D．或5
【答案】C
【解析】因为等腰直角三角形一条直角边所在直线的斜率为，即，
设其倾斜角为，则，
因为斜边与直角边的倾斜角相差45°，则斜边的倾斜角为或，
所以，
，
所以斜边所在直线的斜率为或4．
故选：C．
【方法技巧与总结】
若直线与直线的夹角为，则.
题型七：直线过定点问题
例54．（2022·浙江·高三专题练习）直线经过的定点坐标是______．
【答案】
【解析】把直线的方程改写成：，
由方程组，解得：，所以直线总过定点，
故答案为：
例55．（2022·上海市中国中学高三期中）动直线，恒过的定点是________
【答案】
【解析】∵，
∴
∴，解得：x＝2，y＝2．即方程（a∈R）所表示的直线恒过定点（2，2）．
故答案为：．
例56．（2022·浙江·高三专题练习）已知实数m，n满足，则直线必过定点________________．
【答案】
【解析】由已知得，
代入直线得，
即，
由，解得，
直线必过定点，
故答案为:.
例57．（2022·上海·高三专题练习）对任意的实数，，直线恒经过的一个定点的坐标是________．
【答案】
【解析】由直线整理得
对任意的实数，，直线恒经过的一个定点.
所以，解得
由点代入直线，
满足
所以点在直线上，
即直线恒过定点
故答案为:
例58．（2022·河北·沧县中学高三阶段练习）已知直线恒过定点A，点A在直线上，其中m、n均为正数，则的最小值为（       ）
A．4 B． C．8 D．
【答案】C
【解析】由，得．
∴直线恒过定点，即，
∵点A在直线上，∴，
∴，
当且仅当，即时取等号．∴的最小值为：8．
故选:C．
例59．（2022·陕西·西北工业大学附属中学二模（理））已知向量，，且.若点的轨迹过定点，则这个定点的坐标是（       ）
A． B．
C． D．
【答案】A
【解析】因为，故，整理得到：，
故定点为：.
故选：A.
【方法技巧与总结】
合并参数
题型八：轨迹方程
例60．（2022·全国·高三专题练习）已知，，动点M与A，B两点连线的斜率分别为、，若，求动点M的轨迹方程
【解析】设，则，，又，
∴，
当，且时，恒成立；当时，；
综上，M的轨迹方程为(且)或().
例61．（2022·全国·高三专题练习）过点作两条互相垂直的直线，若交轴于点，交轴于点，求线段的中点的轨迹方程.

【解析】设M（x，y），连结MP，则A（2x，0），B（0，2y），
∵l1⊥l2，∴△PAB为直角三角形，

化简，得x＋2y－5＝0，此即M的轨迹方程.
综上可知，点M的轨迹方程为x＋2y－5＝0.
例62．（2022·全国·高三专题练习）已知是坐标原点，.若点满足，其中，且，求点的轨迹方程.
【解析】设，则，，


即，解得


即
例63．（2022·全国·高三专题练习）直线＝1与x，y轴交点的连线的中点的轨迹方程是________．
【答案】x＋y＝1(x≠0，x≠1)
【解析】
【详解】
直线＋＝1与x，y轴的交点为A(a,0)，B(0,2－a)，
设AB的中点为M(x，y)，
则x＝，y＝1－，
消去a，得x＋y＝1．
∵a≠0且a≠2，∴x≠0且x≠1．
例64．（2022·全国·高三专题练习）在平面直角坐标系中，设三角形ABC的顶点坐标分别为，点在线段OA上（异于端点），设均为非零实数，直线分别交于点E，F，一同学已正确算出的方程：，请你求OF的方程：__________________________．
【答案】
【解析】由截距式可得直线，直线，两式相减得，显然直线AB与CP的交点F满足此方程，又原点O也满足此方程，故为所求的直线OF的方程．
例65．（2022·全国·高三专题练习）直角坐标系中，已知两点，，点满足，其中，且．则点的轨迹方程为（       ）
A． B． C． D．
【答案】A
【解析】由，且λ+μ＝1，
得，
∴，即，则C、A、B三点共线．
设C（x，y），则C在AB所在的直线上，
∵A（2，1），B（4，5），
∴AB所在直线方程为 ，整理得：．
故的轨迹方程为：．
故选：A
【方法技巧与总结】
（1）直接法：寻找决定曲线方程的要素，然后直接写出方程，例如在直线中，若用直接法则需找到两个点，或者一点一斜率
（2）间接法：若题目条件与所求要素联系不紧密，则考虑先利用待定系数法设出曲线方程，然后再利用条件解出参数的值（通常条件的个数与所求参数的个数一致）
题型九：中点公式
例66．（2022·全国·高三专题练习（理））过点P(0,1)作直线l，使它被直线l1：2x＋y－8＝0和l2：x－3y＋10＝0截得的线段被点P平分，则直线l的方程为_________．
【答案】x＋4y－4＝0
【解析】
设l1与l的交点为A(a,8－2a)，求得关于的对称点坐标，利用对称点在直线上求得，即得点坐标，从而得直线方程．
【详解】
设l1与l的交点为A(a,8－2a)，则由题意知，点A关于点P的对称点B(－a,2a－6)在l2上，
代入l2的方程得－a－3(2a－6)＋10＝0，解得a＝4，
即点A(4,0)在直线l上，所以直线l的方程为x＋4y－4＝0.
故答案为：x＋4y－4＝0.
例67．（2022·全国·高三专题练习）过点P(0，1)作直线l，使它被直线l1：和l2：截得的线段恰好被点P平分，求直线l的方程.
【解析】设l1与l的交点为A(a，8-2a)，则由题意知，点A关于点P的对称点B(-a，2a-6)在l2上，
代入l2的方程得:-a-3(2a-6)＋10＝0，解得a＝4，
即点A(4，0)在直线l上，
∴直线l的方程为即x＋4y-4＝0.
例68．（2022·全国·高三专题练习）已知直线 ：过定点，若直线被直线和轴截得的线段恰好被定点平分，求的值.
【解析】
则直线过定点

设直线与直线交于点，与轴交于点，依题意为中点
在中令，则，即
所以，
即，将其代入直线中可得
解之得
【方法技巧与总结】
若点的坐标分别为且线段的中点的坐标为，则
【过关测试】
一、单选题
1．（2022·全国·高三专题练习）若图中的直线l1，l2，l3的斜率分别为k1，k2，k3，则（　　）

A．k1＜k2＜k3 B．k3＜k1＜k2
C．k3＜k2＜k1 D．k1＜k3＜k2
【答案】D
【解析】直线l1的倾斜角α1是钝角，故k1＜0.
直线l2与l3的倾斜角α2与α3均为锐角，且α2＞α3，所以0＜k3＜k2，
因此k1＜k3＜k2.
故选:D.
2．（2022·全国·高三专题练习）直线的倾斜角为（       ）
A．30° B．45° C．60° D．135°
【答案】A
【解析】直线的倾斜角为，
所以直线的斜率为，因为，
则.
故选：A.
3．（2022·全国·高三专题练习）直线过点，其倾斜角为，现将直线绕原点O逆时针旋转得到直线，若直线的倾斜角为，则的值为（       ）
A． B． C．2 D．-2
【答案】B
【解析】由题，，直线的倾斜角为，故
故选：B
4．（2022·上海市实验学校模拟预测）已知点与点在直线的两侧，给出以下结论：
①；
②当时，有最小值，无最大值；
③；
④当且时，的取值范围是.
正确的个数是（       ）
A．1 B．2 C．3 D．4
【答案】B
【解析】将代入有，
而与在的两侧，则，①错误；

由上知：且，则在直线上方与y轴右侧部分，
所以，故无最值，②错误；
由上图知：在直线左上方，则，③正确；
由过且且，即在直线上方与y轴右侧部分，
而表示与连线的斜率，由图知：，④正确.
故选：B
5．（2022·全国·高三专题练习）已知，，三个数成等差数列，直线恒过定点，且在直线上，其中，则的最小值为（       ）
A． B． C．2 D．4
【答案】B
【解析】易知，则，整理得，由解得，
则，则，即，又，则，
则，
当且仅当即时取等，故的最小值为.
故选：B.
6．（2022·全国·高三专题练习）直线过点，且轴正半轴､轴正半轴交于两点，当面积最小时，直线的方程是（       ）
A． B．
C． D．
【答案】C
【解析】根据题意，直线不与轴垂直，则其斜率存在，设为， 则，
因此，直线，
令则有，则，
令则有，则.
因此，

当且仅当即时取等（舍去），
故面积最小值为4，此时，即.
故选：C.
7．（2022·全国·高三专题练习）已知集合，集合，，则的取值范围是（       ）
A． B．且
C．且 D．且且
【答案】C
【解析】集合表示直线上去掉点所构成的两条射线，
在方程中，令可得，
集合表示过定点且斜率存在的直线，
由得两直线斜率不同，则，解得．
故选：C.
8．（2022·河南·高三阶段练习（理））已知直线过定点，直线过定点，与的交点为，则面积的最大值为（       ）
A． B．
C．5 D．10
【答案】C
【解析】由直线的方程是得直线过定点，同理直线方程为，即，所以定点，
又，所以，即在以为直径的圆上，
，由圆的性质知点到的距离最大值等于圆半径，即，
所以面积的最大值为．
故选：C．
二、多选题
9．（2022·湖南·长沙一中高三阶段练习）设直线系：，则下面四个命题正确的是（       ）
A．直线系中包含倾斜角为和的直线
B．点到直线系中的所有直线的距离恒为定值
C．直线系中能构成三角形的任意三条直线所围成的三角形面积都相等
D．存在点不在直线系中的任意一条直线上
【答案】ABD
【解析】当时，直线系：，倾斜角为；当时，直线系：，倾斜角为，故A正确；
点到直线系中的所有直线的距离为，故B正确；
因为点到直线系中的所有直线的距离恒为定值1，
所以直线系中的所有直线均为圆的切线，
取其中4条直线分别为，，，
如图所示，直线所围成的与的面积不相等，故C错；
存在点不在直线系中的任意一条直线上，D正确．
故选：ABD

10．（2022·江苏·高三阶段练习）已知两点，，曲线C上存在点P满足，则曲线的方程可以是（       ）
A． B．
C． D．
【答案】BC
【解析】

由，知点一定在AB的垂直平分线上，
，
因为线段AB的中点坐标为，
所以的方程为.
则满足条件的曲线要与有交点.
与平行，故无交点，选项A错误；
是圆心为，半径的圆，圆心到直线的距离为，故直线与圆相交，故B正确；
把直线与双曲线进行联立，，得，，
所以与双曲线存在交点.故选项C正确；
将直线的方程代入，得，方程无实数解.
故抛物线与直线无交点.故选项D错误；
故选：BC.
11．（2022·重庆·模拟预测）已知直线的方程为，则下列说法中正确的是（       ）
A．当变化时，直线始终经过第二、第三象限
B．当变化时，直线恒过一个定点
C．当变化时，直线始终与抛物线相切
D．当在内变化时，直线可取遍第一象限内所有点
【答案】AC
【解析】由题斜率时，轴截距，此时直线经过第一、第二、第三象限；
斜率时，轴截距，此时直线经过第二、第三、第四象限；故A正确；
当变化时，直线显然不恒过一个定点，故B错误；
联立方程，可得，所以，所以直线与抛物线只有一个交点，
又，所以当变化时，直线始终与抛物线相切，故C正确；
当时，，当且仅当时取等号，所以当在内变化时，直线不可以取遍第一象限内所有点，故D错误．
故选：AC.
12．（2022·江苏·扬州中学高三阶段练习）以下命题正确的是（       ）
A．若直线的倾斜角为，则其斜率为
B．已知，，三点不共线，对于空间任意一点，若，则，，，四点共面
C．不经过原点的直线都可以用方程表示
D．若点在线段（）上运动，则的最大值为
【答案】BD
【解析】对于A：因为倾斜角的取值范围为，当，斜率不存在，故A错误；
对于B：由，，三点不共线，对于空间任意一点，若，则，即，则，，，四点共面，故B正确；
对于C：平行于轴或轴的直线不能用方程表示，故C错误；
对于D：因为点在线段上运动，所以，因为，所以，，所以，故的最大值为，故D正确；
故选：BD
三、填空题
13．（2022·全国·高三专题练习）设直线l过点，在两坐标轴上的截距的绝对值相等，则满足题设的直线l的条数为______条．
【答案】3
【解析】当坐标轴截距为0时，设方程为，
将代入得：，所以方程为；
当坐标轴截距不为0时，设方程为，
则有，解得：，或，
从而方程为或
所以满足题设的直线l的条数为3条.
故答案为：3
14．（2022·全国·高三专题练习）已知直线l被两条直线和截得的线段的中点为，则直线l的一般式方程为______．
【答案】
【解析】设直线l的斜率为，因为直线l过，
所以直线方程为，
由，
由，由题意可知：是截得的线段的中点，
所以，即，
故答案为：
15．（2022·上海市延安中学高三阶段练习）直线：与直线：夹角的正切值为______．
【答案】．
【解析】直线：的斜率为，直线：的斜率为，
设直线：与直线：的夹角为，则，
故答案为：．
16．（2022·上海虹口·二模）设，，三条直线：，：，：，则与的交点到的距离的最大值为_________.
【答案】
【解析】因为，所以，
而直线：即过定点，
：即过定点，
所以与的交点在以为直径的圆上，
圆方程为，即，
所以到的距离的最大值为．
故答案为：．
四、解答题
17．（2022·全国·高三专题练习）求经过（其中）、两点的直线的倾斜角的取值范围．
【解析】由题意，当时，倾斜角，
当时，，即倾斜角为锐角；
综上得：．
18．（2022·全国·高三专题练习）已知直线：，，，若直线与线段恒有公共点，求的取值范围.
【解析】
故直线过定点
如下图所示：

，
若直线与线段恒有公共点，则或
即
19．（2022·全国·高三专题练习（文））已知的斜边为，且.求：
(1)直角顶点的轨迹方程；
(2)直角边的中点的轨迹方程.
【解析】(1)设，因为三点不共线，所以，
因为，所以，
又因为，所以，
整理得，即，
所以直角顶点的轨迹方程为.
(2)设，
因为，是线段的中点，
由中点坐标公式得，所以，
由（1）知，点的轨迹方程为，
将代入得，即
所以动点的轨迹方程为.
20．（2022·全国·高三专题练习）根据所给条件求直线的方程：
（1）过点P(－2，4)且斜率k＝3；
（2）直线过点(－3，4)，且在两坐标轴上的截距之和为12.
【解析】（1）由题设知，直线l的方程为y－4＝3(x＋2)，即3x－y＋10＝0.
（2）由题设知：横、纵截距均不为0，故可设直线方程为.
∵直线过点(－3，4)，
∴，解得a＝－4或9.
故所求直线方程为4x－y＋16＝0或x＋3y－9＝0.
21．（2022·全国·高三专题练习）已知直线与直线的交点为.
（1）若直线过点，且点和点到直线的距离相等，求直线的方程；
（2）若直线过点且与轴和轴的正半轴分别交于，两点，的面积为，求直线的方程．
【解析】（1）由 得 即交点．
由直线过点，且点和点到直线的距离相等，
可知或过的中点．
当由得，
所以直线的方程为即.
当直线过的中点时，直线的方程为.
综上所述：直线的方程为或．
(2)由题可知直线的横、纵截距，都存在，且，，
则.又直线过点，的面积为，
所以，解得，
故直线的方程为，即.
22．（2022·全国·高三专题练习）已知，，，求的最大值.
【解析】将变形，得，
显见是直线（，）过定点.
如图.

设
显然有：，，
，，其中.
∴
故







，
当且仅当，即时，取得最大值.