

2022-2023学年上海市曹杨中学高二上学期期中数学试题(解析版)
展开2022-2023学年上海市曹杨中学高二上学期期中数学试题
一、单选题
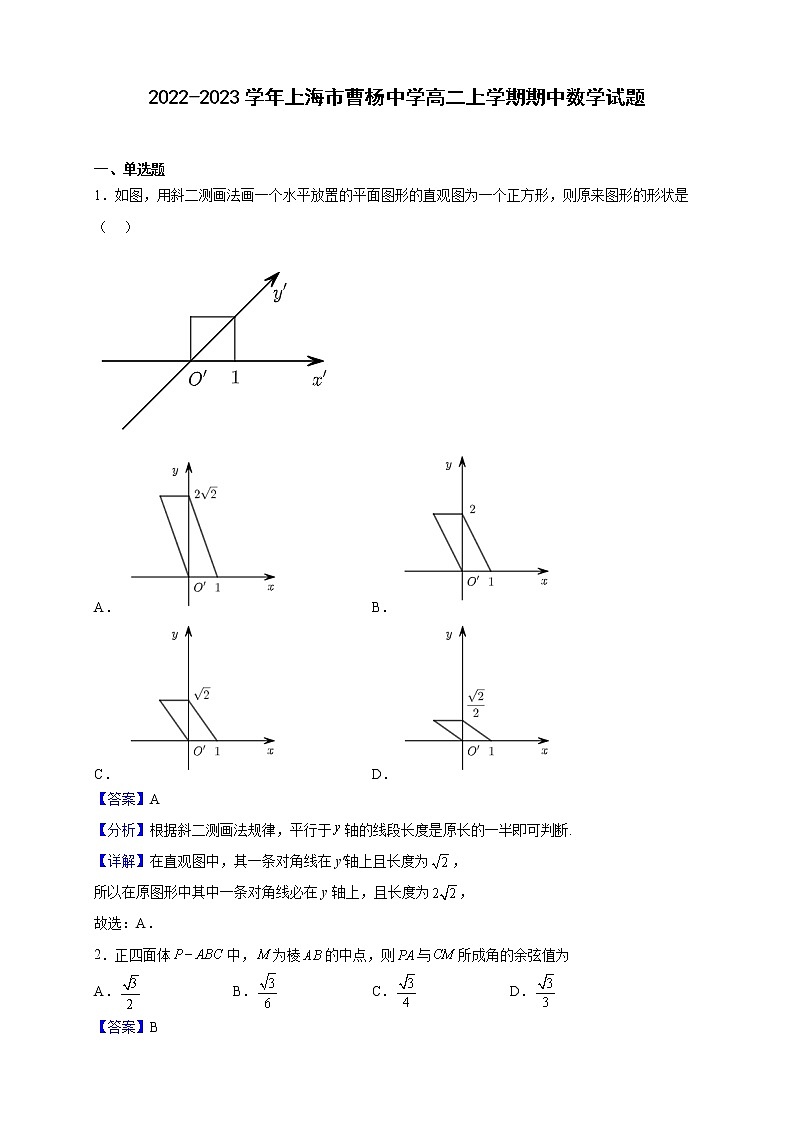
1.如图,用斜二测画法画一个水平放置的平面图形的直观图为一个正方形,则原来图形的形状是( )
A. B.
C. D.
【答案】A
【分析】根据斜二测画法规律,平行于轴的线段长度是原长的一半即可判断.
【详解】在直观图中,其一条对角线在y′轴上且长度为,
所以在原图形中其中一条对角线必在y轴上,且长度为,
故选:A.
2.正四面体中,为棱的中点,则与所成角的余弦值为
A. B. C. D.
【答案】B
【详解】试题分析:如图,
取中点 ,连接.为与所成的角(或所成角的补角),设,则,由余弦定理得:∴ ;故选B.
【解析】异面直线及其所成的角.
【方法点睛】过空间任意一点引两条直线分别平行于两条异面直线,它们所成的锐角(或直角)就是异面直线所成的角.求两条异面直线所成角的大小一般方法是通过平行移动直线,把异面问题转化为共面问题来解决.
3.已知m、n为不同的直线,为不同的平面.则下列命题中错误的是( )
A.m,n是内两相交直线,则与相交的充要条件是m,n至少有一条与相交;
B.m,n为异面直线,过空间任一点P,一定能作一条直线l与m,n都垂直;
C.与l都不垂直,则m与n一定不垂直;
D.m,n为异面直线、过空间任一点P,一定能作一条直线l与m,n都相交.
【答案】D
【分析】根据点线面的位置关系对选项一一判断即可.
【详解】对A,若与相交,设交线为,所以m,n至少有一条与相交,故m,n至少有一条与相交;
若m,n至少有一条与相交,则与相交;故A正确;
对B,因为m,n为异面直线,故作直线,且与相交,设,过空间任一
点P,一定能作一条直线l与垂直,所以一定能作一条直线l与m,n都垂直,B正确;
对C,由于设且,则,故
假设,又,与相交,且,则,故与已知矛盾,
所以m与n一定不垂直,C正确;
对D,设且,当时,不能作一条直线l与m,n都相交,故D错误;
故选:D.
4.在三棱锥中,平面;记直线与直线所成的角为,直线与平面所成的角为,二面角的平面角为,则( )
A. B.
C. D.
【答案】A
【分析】先得到三棱锥的每一个面都是直角三角形,然后可得与平面所成的角,二面角的平面角,在直角三角形中算出他们的余弦值,利用向量法计算直线与直线所成的角为的余弦值,然后比较大小.
【详解】令,
由平面,且平面
,又,,
面
三棱锥的每一个面都是直角三角形.
与平面所成的角,
二面角的平面角,
由已知可得,
,
,
又,
则
所以,又均为锐角,
故选:A.
二、填空题
5.如果异面直线、所成角为,那么的取值范围是_____________.(用弧度表示)
【答案】.
【分析】用异面直线所成角的定义判断.
【详解】过空间任意一点引两条直线分别平行于两条异面直线,它们所成的锐角(或直角)就是异面直线所成的角,故两异面直线所成角的范围是.
故答案为:.
6.若的夹角为,则___________.
【答案】0.5
【分析】先求出,进而由求出答案.
【详解】因为的夹角为,所以,于是.
故答案为:.
7.正四棱柱的底面边长为10,侧面积为40,则这个棱柱的体积为_____________.
【答案】100
【分析】根据侧面积公式求出棱柱的高,根据底面边长求出底面积,代入体积公式得出体积.
【详解】设棱柱的底面边长为,高为,
则,侧面积,解得.
正四棱柱的体积.
故答案为:100.
8.圆柱的轴截面是正方形,且面积为16,则圆柱的侧面积为_____________.
【答案】
【分析】根据圆柱的轴截面几何性质可得圆柱的底面半径与高度,从而可求圆柱的侧面积.
【详解】解:圆柱的轴截面是正方形,且面积为16,则该圆柱的底面直径为4,高为4
即底面半径,高
所以圆柱的侧面积.
故答案为:.
9.体积为64的正方体的顶点都在同一球面上,则该球的表面积为_____________.
【答案】
【分析】根据正方体的体积公式,求得棱长,结合球与正方体的对称性,求正方体的体对角线,可得球的半径,利用球的表面积公式,可得答案.
【详解】设正方体的棱长为,则体积,即,
易知正方体的体对角线为外接球的直径,设外接球的半径为,则,即,
故该球的表面积.
故答案为:.
10.如图是长方体被一平面截得的几何体,四边形为截面,则四边形的形状为________.
【答案】平行四边形
【详解】∵平面ABFE∥平面CDHG,平面EFGH∩平面ABFE=EF,平面EFGH∩平面CDHG=HG,∴EF∥HG.同理,EH∥FG,∴四边形EFGH是平行四边形.
【解析】面面平行的性质定理的运用.
11.将一个边长为2的正三角形以其一边所在直线为旋转轴旋转一周,所得几何体的表面积为_____________.
【答案】
【分析】根据正三角形绕一边所在直线为旋转轴旋转一周,得到几何体是两个同底的圆锥求解.
【详解】如图所示:正三角形绕AB所在直线为旋转轴旋转一周,得到几何体是两个同底的圆锥,
圆锥的底面半径为,
所以所得几何体的表面积为,
故答案为:
12.己知A,B,C三点都在体积为的球O的表面上,若,则球心O到平面ABC的距离为_____________.
【答案】3
【分析】根据球的体积公式可得球的半径,结合条件可得的外接圆的半径,然后根据球的性质即得.
【详解】设球的半径为R,则,
解得,
设的外接圆的半径为,因为,
所以,即,
∴球心到平面的距离.
故答案为:3.
13.如图,平行六面体的底面是边长为1的正方形,且,,则线段的长为_________.
【答案】
【分析】以、、为基底表示出,再根据数量积的运算律计算可得.
【详解】解:因为,
所以
,所以.
故答案为:
14.边长为5的正方形EFGH是圆柱的轴截面,则从点E沿圆柱的侧面到相对顶点G的最短距离为________.
【答案】
【分析】作出圆柱的侧面展开图,利用勾股定理即可求解.
【详解】如图,矩形E1F1GH是圆柱沿着其母线EF剪开半个侧面展开而得到的,
则从点E沿圆柱的侧面到相对顶点G的最短距离为.
由题意可知GH=5,,
所以
所以从点E沿圆柱的侧面到相对顶点G的最短距离是.
故答案为:.
15.设异面直线a、b所成的角为,经过空间一点O有且只有两条直线与异面直线a、b成等角,则的取值范围为_____________.
【答案】
【分析】先作出直线所成角,再结合图象以及对称性求得的取值范围.
【详解】过作,则所成的角即异面直线所成角,
确定一个平面,过作,
过作直线和直线分别平分形成的两个对顶角,
当过的直线在平面内旋转时,与所成的角为,且;
当过的直线在平面内旋转时,与所成的角为,且;
结合对称性可知:若经过空间一点O有且只有两条直线与异面直线a、b成等角,
则的取值范围为.
故答案为:
16.如图,已知棱长为2的正方体中,点在线段上运动,给出下列结论:
①异面直线与所成的角范围为;
②平面平面;
③点到平面的距离为定值;
④存在一点,使得直线与平面所成的角为.
其中正确的结论是___________.
【答案】②③
【解析】数形结合说明异面直线与所成的角的范围为,故①错误;证明平面,所以平面平面,故②正确;点到平面的距离为定值,且等于的,即,故③正确;与平面所成的角为,最大值为,故④不正确.
【详解】对于①,当在点时,,
异面直线与所成的角最大为,
当在点时,异面直线与所成的角最小为,
所以异面直线与所成的角的范围为,故①错误;
对于②,如图,因为平面,所以,同理,又因为平面,所以平面,所以平面平面,故②正确;
对于③,因为平面,平面,所以平面,所以点到平面的距离为定值,且等于的,即,故③正确;
对于④,直线与平面所成的角为,,
当时,最小,最大,最大值为,故④不正确,
故答案为:②③.
【点睛】关键点睛:解答本题的关键是判断命题①④的真假,它们都是求空间的角,它们都是利用数形结合的方法求空间角的最值,对于数形结合的这种数学思想要注意灵活运用.
三、解答题
17.
(1)请用文字语言叙述异面直线的判定定理;
(2)把(1)中的定理写成“已知:...,求证:...”的形式,并用反证法证明.
【答案】(1)见解析;
(2)见解析.
【分析】(1)将判定定理用文字表述即可;
(2)根据(1)中的前提和结论可得定理的形式,利用反证法可证该结论.
【详解】(1)
异面直线的判定定理:平面外一点与平面内一点的连线与平面内不过该点直线是异面直线.
(2)(1)中的定理写成“已知:...,求证:...”的形式如下:
,求证:为异面直线.
证明:若不为异面直线,则共面于,故
而,故为同一平面,而,故,
这与矛盾,故为异面直线.
18.如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离.
【答案】(1)证明见解析;
(2).
【分析】(1)证明、,由线面垂直的判定定理可证明平面,即证;
(2)由勾股定理求出△ACD1各个边长,设点到平面的距离为,由即可求解.
【详解】(1)因为平面,平面,
所以,
因为四边形是矩形,,
所以四边形是正方形,
所以,
又平面,平面,,
所以平面,又因为平面,
所以.
(2)因为,,为的中点,
所以,,,,
所以,,
设点到平面的距离为,
由可得:,
即,
解得:,
所以点E到面ACD1的距离为.
19.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3.
(1)请估算出堆放的米约有多少斛?
(2)若要建造一个底部直径为4尺的家用圆柱形储粮仓,试问储粮仓的高至少为多少尺,才可以将这堆米全部放入?(结果均保留整数)
【答案】(1);
(2)储粮仓的高至少为3尺,才可以将这堆米全部放入.
【分析】(1)根据米堆底部的弧长可求出圆锥的底面半径,再根据圆锥的体积公式求出米堆的体积,从而可求解;
(2)根据圆柱的体积公式列式求解即可.
【详解】(1)设圆锥底面半径为,则,所以,
所以米堆的体积为.
故堆放的米约为.
(2)设储粮仓的高为,则,所以尺.
所以储粮仓的高至少为3尺,才可以将这堆米全部放入.
20.如图,四面体ABCD中,AD、BD、CD两两垂直,且,过AB上的动点E(不同于A、B两点)作平行于AD、BC的平面,分别交棱BD、CD、AC于F、G、H三点.
(1)求异面直线EF与AC所成角的大小;
(2)若E为AB中点,求点E到直线CD的距离;
(3)若直线CE与平面ABD所成角的正切值为,求此时直线AB与平面CDE所成角的大小.
【答案】(1);
(2);
(3).
【分析】(1)利用线面平行的性质证得,再由异面直线所成角的定义计算作答.
(2)根据给定条件,证明平面,求出DE长即可作答.
(3)根据给定条件,确定点E的位置,再求线面角的大小作答.
【详解】(1)因平面,平面,平面平面,则,
因此是异面直线EF与AC所成的角,而,有,即,
所以异面直线EF与AC所成角的大小为.
(2)因平面,则平面,连接DE,如图,
平面,因此,即DE长为点E到直线CD的距离,而E为AB中点,
中,,
所以点E到直线CD的距离为.
(3)由(2)知,平面,是直线CE与平面ABD所成的角,而,
即有, 得,而的斜边AB上的高,
因此DE是的斜边AB上的高,即,由平面,平面,得,
平面CDE,于是得平面CDE,
所以直线AB与平面CDE所成角的大小为.
21.如图,在正四棱锥中,,分别为的中点,平面与棱的交点为.
(1)求异面直线与所成角的大小;
(2)求平面与平面所成锐二面角的大小;
(3)求点的位置.
【答案】(1)
(2)
(3)点的位置为线段PC靠近P的三等分点.
【分析】(1)作出辅助线,找到异面直线与所成的角是∠OEA(或补角),利用余弦定理求出;
(2)作出辅助线,找到平面与平面所成锐二面角为,经过计算得到;
(3)证明出A、Q、G三点共线,利用第二问的求出的,和题干中的条件确定点的位置.
【详解】(1)连接AC,BD,相交于点O,
因为四边形ABCD是正方形,所以O是正方形的中心,连接PO,
因为四棱锥是正四棱锥,则PO⊥底面ABCD,连接OE,
因为为的中点,所以EO是△PBD的中位线,所以EO∥PD,
∠OEA(或补角)即为异面直线与所成角的大小,
因为正四棱锥中,,所以△PAB是等边三角形,
所以,由勾股定理得:,所以,
因为,E为PB的中点,所以,
在△AOE中,由余弦定理得:,
所以异面直线与所成角的大小为
(2)连接EF,与OP相交于点Q,则Q为OP,EF的中点,
因为分别为的中点,所以EF是三角形PBD的中位线,所以EF∥BD,
因为平面ABCD,平面ABCD,所以EF∥平面ABCD,
设平面与平面相交于直线,故EF∥∥DB,连接QA,
则因为AE=AF,所以AQ⊥EF,又因为OA⊥BD,
故∠QAO即为平面与平面所成锐二面角,其中,,所以,故,
即平面与平面所成锐二面角的大小为
(3)延长AQ,则由两平面相交的性质可得AQ一定过点G,
过点G作GM∥PO交AC于点M,因为PO⊥底面ABCD,所以GM⊥底面ABCD,
设GM=CM=x,则AM=4-x,由第二问知:,
所以,即,解得:,
故,所以点的位置为线段PC靠近P的三等分点.
2022-2023学年上海市曹杨中学高二下学期期中数学试题含答案: 这是一份2022-2023学年上海市曹杨中学高二下学期期中数学试题含答案,共12页。试卷主要包含了填空题,单选题,解答题等内容,欢迎下载使用。
2022-2023学年上海市曹杨第二中学高二上学期期末数学试题含解析: 这是一份2022-2023学年上海市曹杨第二中学高二上学期期末数学试题含解析,共16页。试卷主要包含了填空题,单选题,解答题等内容,欢迎下载使用。
2022-2023学年上海市曹杨第二中学高一上学期期中数学试题(解析版): 这是一份2022-2023学年上海市曹杨第二中学高一上学期期中数学试题(解析版),共11页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












