2023年高考数学二轮复习重点基础练习：专题四 考点12 函数模型及其应用（B卷）

这是一份2023年高考数学二轮复习重点基础练习：专题四 考点12 函数模型及其应用（B卷），共8页。试卷主要包含了有一组试验数据如下表所示等内容，欢迎下载使用。
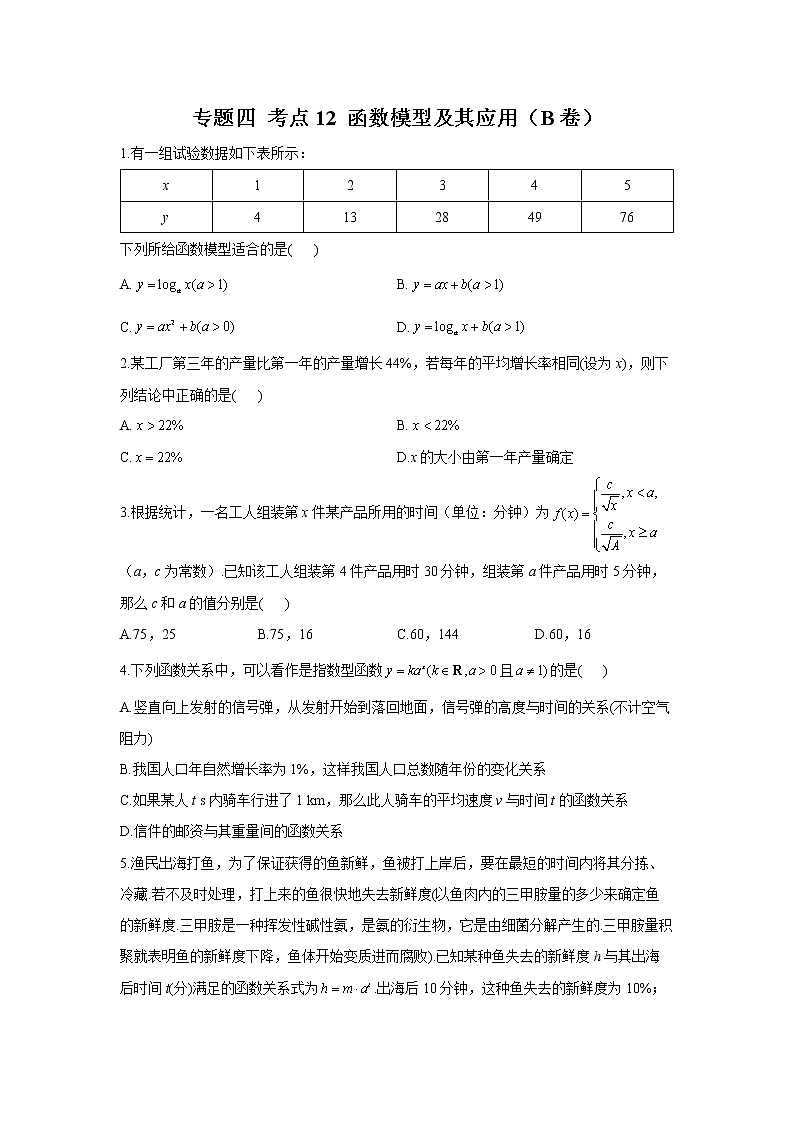
专题四 考点12 函数模型及其应用（B卷）1.有一组试验数据如下表所示：x12345y413284976下列所给函数模型适合的是(   )A.  B.C.  D.2.某工厂第三年的产量比第一年的产量增长44%，若每年的平均增长率相同(设为x)，则下列结论中正确的是(   )A.  B.C.  D.x的大小由第一年产量确定3.根据统计，一名工人组装第x件某产品所用的时间（单位：分钟）为（a，c为常数）.已知该工人组装第4件产品用时30分钟，组装第a件产品用时5分钟，那么c和a的值分别是(   )
A.75，25 B.75，16 C.60，144 D.60，164.下列函数关系中，可以看作是指数型函数且的是(   )A.竖直向上发射的信号弹，从发射开始到落回地面，信号弹的高度与时间的关系(不计空气阻力)
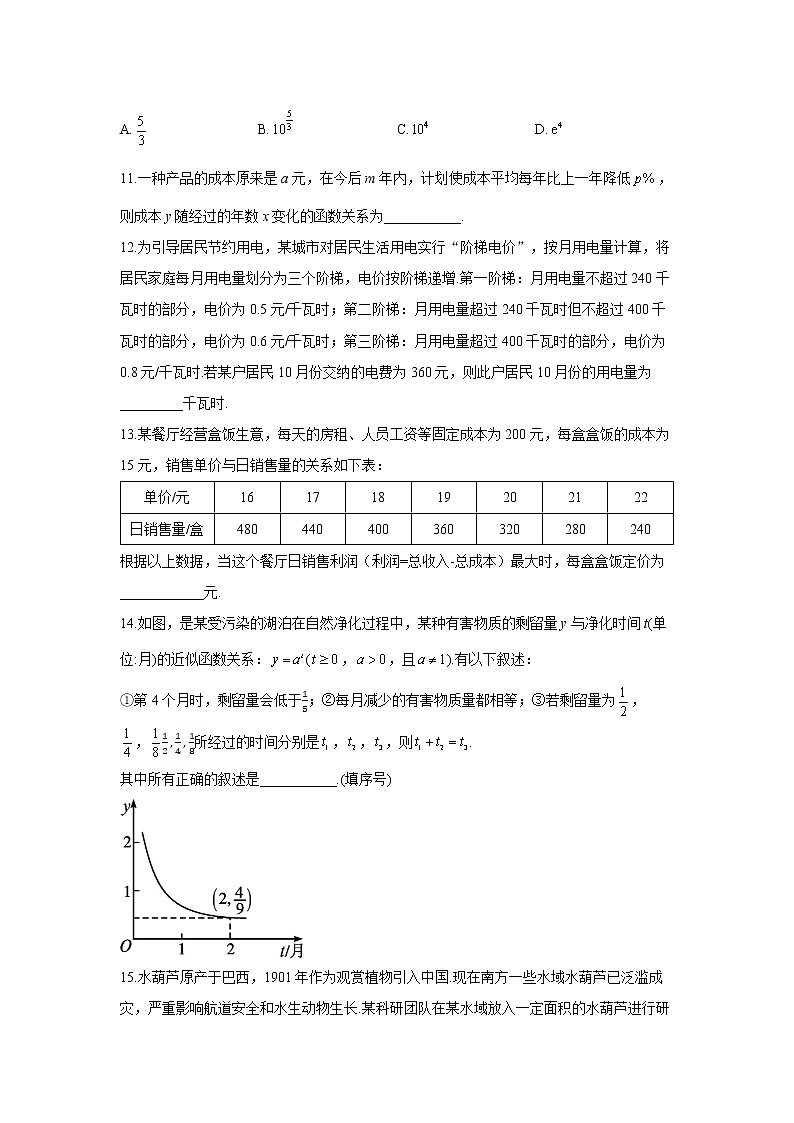
B.我国人口年自然增长率为1%，这样我国人口总数随年份的变化关系C.如果某人t s内骑车行进了1 km，那么此人骑车的平均速度v与时间t的函数关系D.信件的邮资与其重量间的函数关系5.渔民出海打鱼，为了保证获得的鱼新鲜，鱼被打上岸后，要在最短的时间内将其分拣、冷藏.若不及时处理，打上来的鱼很快地失去新鲜度(以鱼肉内的三甲胺量的多少来确定鱼的新鲜度.三甲胺是一种挥发性碱性氨，是氨的衍生物，它是由细菌分解产生的.三甲胺量积聚就表明鱼的新鲜度下降，鱼体开始变质进而腐败).已知某种鱼失去的新鲜度h与其出海后时间t(分)满足的函数关系式为.出海后10分钟，这种鱼失去的新鲜度为10%；出海后20分钟，这种鱼失去的新鲜度为20%.若不及时处理，则这种鱼从出海到失去全部新鲜度经过了(已知，结果取整数)(   )A.33分 B.43分 C.50分 D.56分6.某地由于人们健康水平的不断提高，某种疾病的患病率正以每年的比例降低.若要求患病率低于当前患病率的，则至少需要经过的时间为(   )(参考数据：，)A.4年 B.5年 C.6年 D.7年7.我国古代著名的思想家庄子在《庄子·天下篇》中说：“一尺之棰，日取其半，万世不竭.”用现代语言叙述为：一尺长的木棒，每天取其一半，永远也取不完.这样，每天剩下的部分都是前天的一半.如果把“一尺之棰”看成单位“1”，那么x天后剩下的部分y与x的函数关系式为(   )A. B. C. D.8.中国的5G技术处于领先地位，5G技术的数学原理之一便是著名的香农公式：.它表示：在受噪声干扰的信道中，最大信息传递速度C取决于信道带宽W，信道内信号的平均功率S，信道内部的高斯噪声功率N的大小，其中叫作信噪比.当信噪比比较大时，公式中真数中的1可以忽略不计.按照香农公式，若不改变带宽W，而将信噪比从1000提升至4000，则C大约增加了（附：）(   )A.10% B.20% C.50% D.100%9.在一定的储存温度范围内，某食品的保鲜时间y（单位：小时）与储存温度x（单位：℃）之间满足函数关系（为自然对数的底数，k，b为常数），若该食品在0℃时的保鲜时间为120小时，在30℃时的保鲜时间为15小时，则该食品在20℃时的保鲜时间为(   )A.30小时 B.40小时 C.50小时 D.80小时10.当强度为x的声音对应的等级为分贝时，有 (其中为常数).装修时电钻发出的声音约为100分贝，普通室内谈话的声音约为60分贝.则装修时电钻发出的声音强度与普通室内谈话的声音强度的比值为(   )A. B. C. D.11.一种产品的成本原来是a元，在今后m年内，计划使成本平均每年比上一年降低，则成本y随经过的年数x变化的函数关系为___________.12.为引导居民节约用电，某城市对居民生活用电实行“阶梯电价”，按月用电量计算，将居民家庭每月用电量划分为三个阶梯，电价按阶梯递增.第一阶梯：月用电量不超过240千瓦时的部分，电价为0.5元/千瓦时；第二阶梯：月用电量超过240千瓦时但不超过400千瓦时的部分，电价为0.6元/千瓦时；第三阶梯：月用电量超过400千瓦时的部分，电价为0.8元/千瓦时.若某户居民10月份交纳的电费为360元，则此户居民10月份的用电量为_________千瓦时.13.某餐厅经营盒饭生意，每天的房租、人员工资等固定成本为200元，每盒盒饭的成本为15元，销售单价与日销售量的关系如下表：单价/元16171819202122日销售量/盒480440400360320280240根据以上数据，当这个餐厅日销售利润（利润=总收入-总成本）最大时，每盒盒饭定价为____________元.14.如图，是某受污染的湖泊在自然净化过程中，某种有害物质的剩留量y与净化时间t(单位:月)的近似函数关系：(，，且).有以下叙述：①第4个月时，剩留量会低于；②每月减少的有害物质量都相等；③若剩留量为，，所经过的时间分别是，，，则.其中所有正确的叙述是___________.(填序号)15.水葫芦原产于巴西，1901年作为观赏植物引入中国.现在南方一些水域水葫芦已泛滥成灾，严重影响航道安全和水生动物生长.某科研团队在某水域放入一定面积的水葫芦进行研究，发现其蔓延速度越来越快，经过2个月覆盖面积为18 ，经过3个月覆盖面积为27 .现水葫芦覆盖面积y(单位：)与经过时间个月的关系有两个函数模型与可供选择.(1)试判断哪个函数模型更合适，并求出该模型的解析式；(2)求原先投放的水葫芦的面积并求约经过几个月该水域中水葫芦面积是当初投放的1000倍.(参考数据：，，，)
答案以及解析1.答案：C解析：通过题中所给数据可知，随着x的增大，y的增长速度越来越快，而A，D中的函数增长速度越来越慢，B中的函数增长速度保持不变，故选C.2.答案：B解析：由题意设第一年的产量为a，则第三年的产量为，解得.故选B.3.答案：C解析：显然，则由题意可得解得故选C.4.答案：B解析：A：竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系是二次函数关系；B：我国人口年自然增长率为1%，这样我国人口总数随年份的变化关系是指数型函数关系；C：如果某人t s内骑车行进了1 km，那么此人骑车的平均速度v与时间t的函数关系是反比例函数关系；D：信件的邮资与其重量间的函数关系是一次函数关系.故选B.5.答案：B解析：依题设有解得，，故.令，得，故(分).6.答案：B解析：假设至少需要经过的时间为x(单位：年)，由题意得，两边取以为底的对数得，.因为，所以，.故选B.7.答案：D解析：由题意可得，剩下的部分依次为，，，…，因此x天后剩下的部分y与x的函数关系式为，故选D.8.答案：B解析：将信噪比从1000提升至4000时，C增加了，故C大约增加了20%，故选B.9.答案：A解析：由题意可得解得，所以当时，.故选A.10.答案：C解析：设装修时电钻发出的声音强度为，普通室内谈话的声音强度为.由题意得所以装修时电钻发出的声音强度与普通室内谈话的声音强度的比值为.11.答案：(，且)解析：由成本经过x年降低到y元，得(，且).12.答案：580解析：设某户居民一个月的用电量为x千瓦时，电费为元，则当时，；当时，；当时，.故根据10月份此户居民交纳的电费可知，此户居民用到了第三阶梯电量，令，得.所以此户居民10月份的用电量为580千瓦时.13.答案：21.5解析：由题表信息可知，销售单价为16元时，日销售量为480盒，销售单价每增加1元，日销售量减少40盒，设销售单价为x元，则日销售量为盒，设这个餐厅的日销售利润为y元，则，所以当时，y取得最大值，最大值为1490，即每盒盒饭定价为21.5元时，日销售利润最大.14.答案：①③解析：由图象可知，当时，，即，解得.故.所以当时，有害物质的剩留量为，所以①正确.
第一个月的减少量为；第二个月的减少量为，显然两者不同，所以②错误.
③由已知，，，所以.即，所以，故③正确.15.解析：(1)应选函数，(2)原先投放的水葫芦的面积为8 ，约经过17个月该水域中水葫芦面积是当初投放的1000倍解析：(1)函数中，y随x的增长而增长，速度越来越快，函数中，y随x的增长而增长，速度越来越慢，依题意应选函数.则有解得.(2)由(1)知，当时，.设经过x个月该水域中水葫芦面积是当初投放的1000倍，则有，.故原先投放的水葫芦的面积为8 ，约经过17个月该水域中水葫芦面积是当初投放的1000倍.