2023年高考数学二轮复习重点基础练习：专题四 考点10 函数的图象（A卷）

专题四 考点10 函数的图象（A卷）

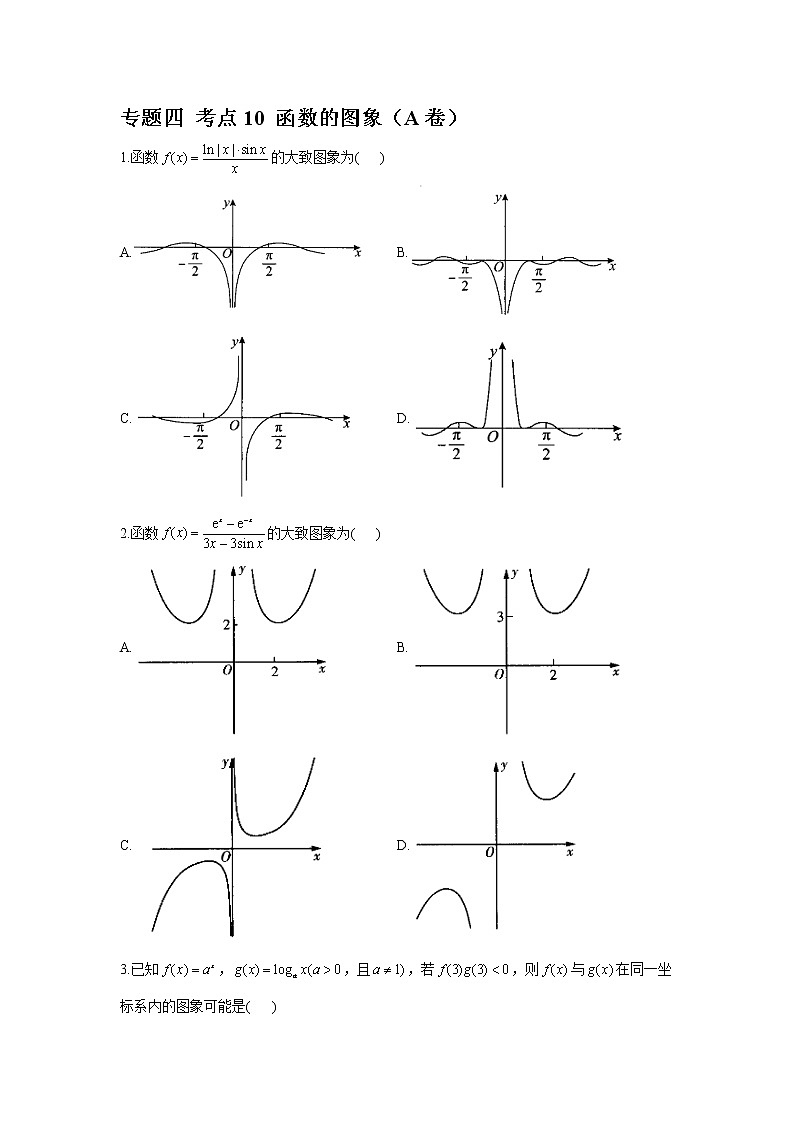
1.函数的大致图象为(   )

A. B.

C. D.

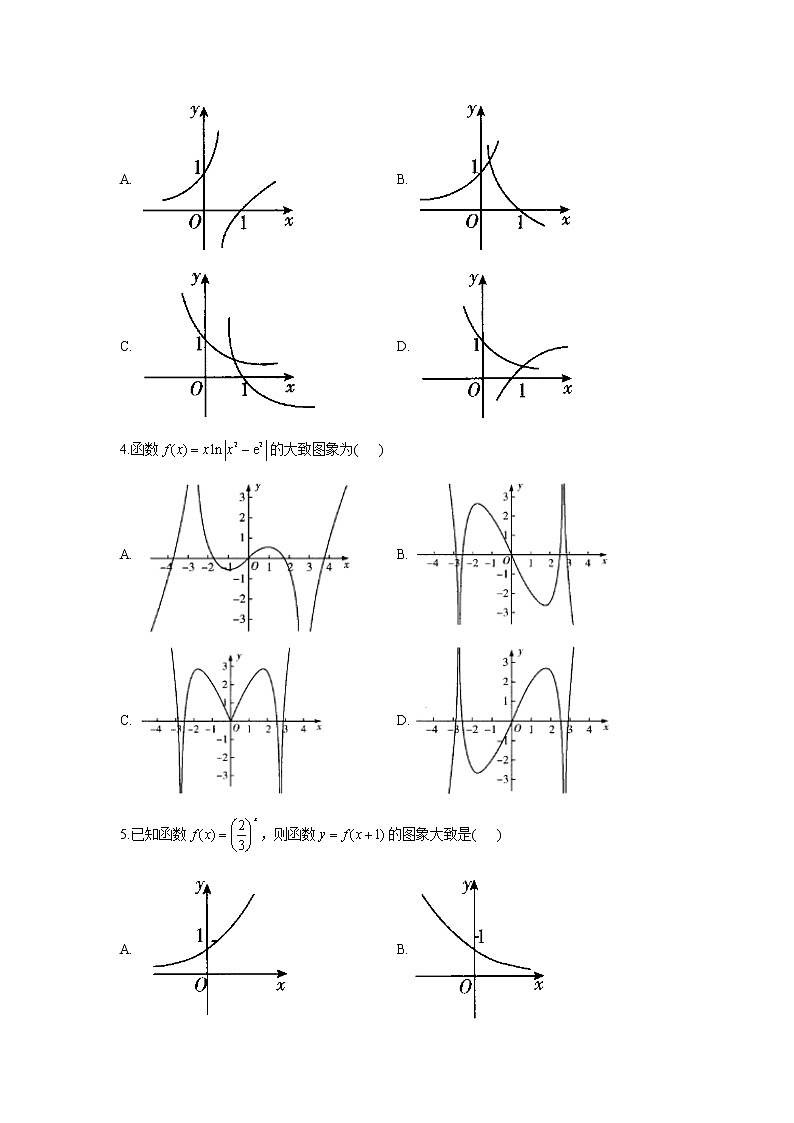
2.函数的大致图象为(   )

A. B.

C. D.

3.已知，，且，若，则与在同一坐标系内的图象可能是(   )

A. B.

C. D.

4.函数的大致图象为(   )

A. B.

C. D.

5.已知函数，则函数的图象大致是(   )

A. B.

C. D.

6.函数在上的图象大致是(   )

A. B.

C. D.

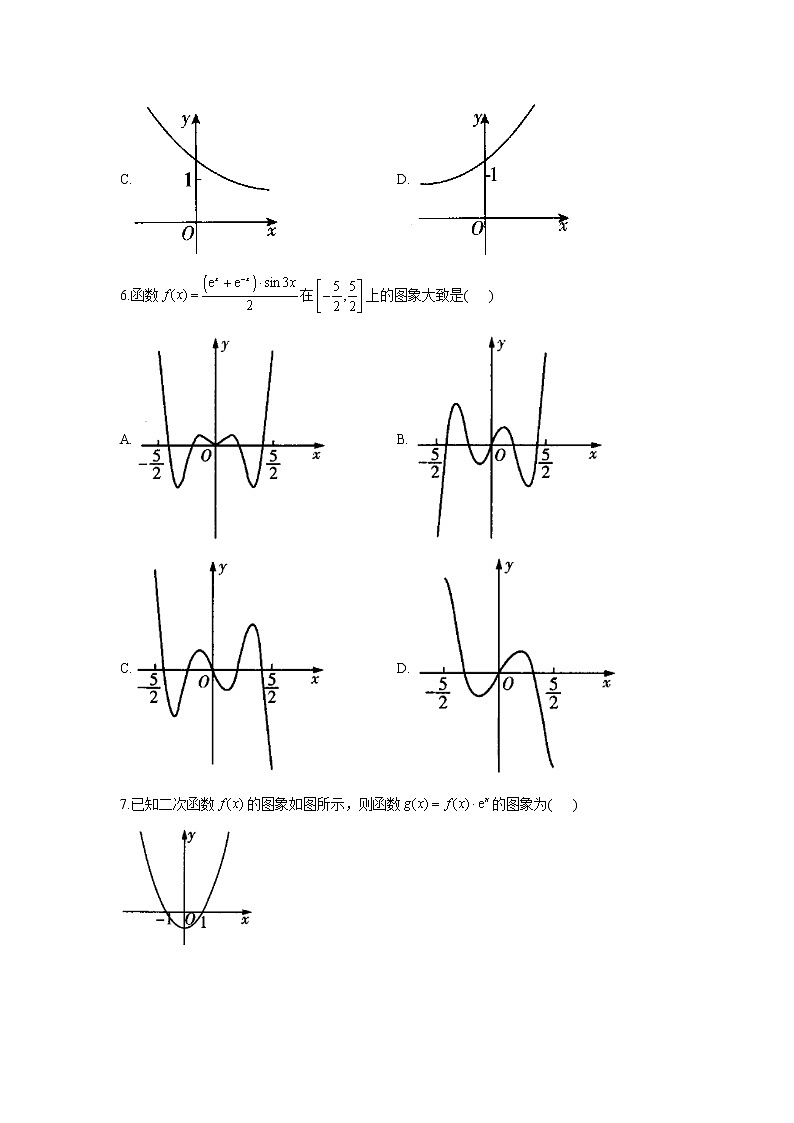
7.已知二次函数的图象如图所示，则函数的图象为(   )

A. B.

C. D.

8.函数的图象大致是(   )

A. B.

C. D.

9.函数的图象可能是(   )

A. B.

C. D.

10.函数在区间上的图象可能是(   )

A. B.

C. D.

11.函数（且）的大致图象是(   )

A. B.

C. D.

12.函数的大致图象是(   )

A. B.

C. D.

13.函数的图象是(   )

A. B.

C. D.

14.某高三学生于2020年9月第二个周末乘高铁赴济南参加全国高中数学联赛（山东省赛区）的比赛活动.早上他乘坐出租车从家里出发，离开家不久，发现身份证忘在家里了，于是回到家取上身份证，然后乘坐出租车以更快的速度赶往高铁站，令x（单位：分钟）表示他离开家的时间，y（单位：千米）表示离开家的距离，其中等待红绿灯及在家取身份证的时间忽略不计，出租车匀速行驶，则下列图象中与上述事件吻合最好的是(   )

A. B.

C. D.

15.函数在的图象大致为(   )

A. B.

C. D.

答案以及解析

1.答案：A

解析：由题，函数的定义域为，，所以函数为偶函数，图象关于y轴对称，故排除C；当时，，故排除D；当时，，故排除B.故选A.

2.答案：A

解析：因为函数的定义域为，，所以为偶函数，排除选项C，D；因为，所以排除选项B.故选A.

3.答案：C

解析：由指数函数和对数函数的单调性知，函数与，且在上的单调性相同，可排除B，D.再由关系式可排除A，故选C.

4.答案：D

解析：由题得函数的定义域为，且，

所以函数为奇函数，排除选项C；

又，排除选项A，B.故选D.

5.答案：B

解析：函数是单调递减函数，将函数的图象向左平移1个单位长度即可得函数的图象，该函数图象与y轴的交点在的下方，只有B的图象符合，故选B.

6.答案：B

解析：，是奇函数，排除A.当时，，排除C.由得，又，或或，在上有5个零点，排除D.故选B.

7.答案：A

解析：由函数的图象结合题意知，当或时，；当时，，由选项可知选A.

8.答案：A

解析：当时，单调递增，所以在上单调递增，排除B，C；当时，，则在上单调递减，所以在上单调递减，排除D.选A.

9.答案：A

解析：易知函数的定义域关于原点对称，且，

则函数是奇函数，图象关于原点对称，排除B，D；

，排除C，故选A.

10.答案：A

解析：令，则，又其定义域为，关于原点对称，故为奇函数，其图象关于原点对称，排除C，D.当时，，，故，排除B.故选A.

11.答案：C

解析：依题意，由此判断出正确的选项为C.故选C.

12.答案：B

解析：法一：由题可知，当时，，其图象可由函数的图象向右平移1个单位得到；当时，，其图象可由函数的图象先关于y轴做翻折变换，再向左平移1个单位得到，结合选项可知B正确.故选B.

法二：易知的定义域为，又，所以是偶函数，因此C，D错误.

当时，，是上的增函数，故选B.

13.答案：B

解析：当时，，排除C，D；

当时，，又与的图象关于原点对称，故选B.

14.答案：C

解析：由题意知，该高三学生从家出发去高铁站，y是x的一次函数，且斜率为正；他返回家取身份证的过程中，y仍然是x的一次函数，斜率为负；他最后从家到高铁站，y仍然是x的一次函数，斜率为正值，且斜率比第一段的斜率大，结合图象可知，与题干中事件吻合最好的图象为C.故选C.

15.答案：B

解析：设，则，为奇函数，排除选项C；当时，，排除选项D；当时，，排除选项A.故选B.