2023年高考数学二轮复习重点基础练习：专题八 考点20 平面向量的概念、线性运算与基本定理（A卷）

这是一份2023年高考数学二轮复习重点基础练习：专题八 考点20 平面向量的概念、线性运算与基本定理（A卷），共6页。试卷主要包含了若O是内的一点，且，则O是的，在中，，若，则点P在，向量等内容，欢迎下载使用。
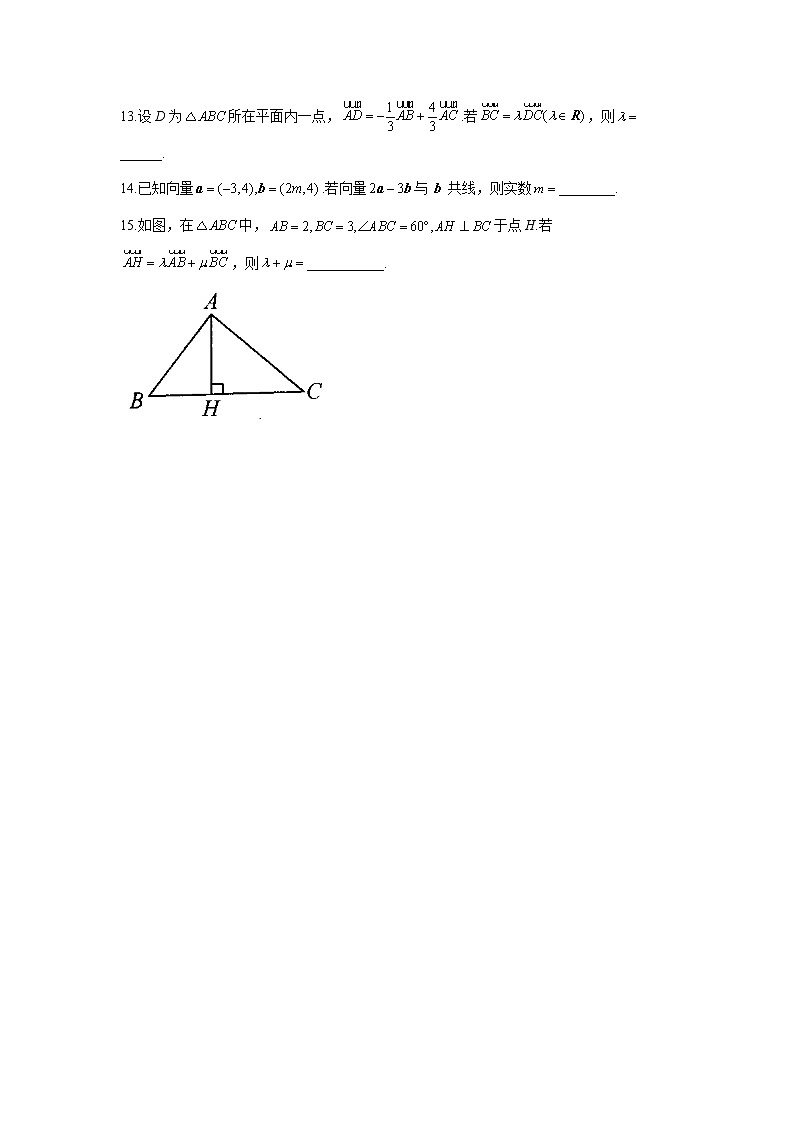
考点20 平面向量的概念、线性运算与基本定理（A卷）1.若，且，则四边形ABCD的形状为(   )A.平行四边形  B.矩形C.菱形  D.等腰梯形2.在平行四边形ABCD中，E为AC的三等分点(靠近点A)，连BE并延长，交AD于H，则(   )A. B. C. D.3.若O是内的一点，且，则O是的(   )A.重心 B.垂心 C.内心 D.外心4.在中，，若，则点P在(   )A.平分线所在直线上 B.线段AB垂直平分线上C.AB边所在直线上  D.AB边的中线上5.如图所示，在正方形ABCD中，E为AB的中点，F为CE的中点，则(   )A.  B.C.  D.6.设向量，且的方向相反，则x的值是(   )A.2 B.-2 C. D.07.向量.若A，B，C三点共线，则k的值为(   )A.-2 B.11 C.-2或11 D.2或-118.在四面体OABC中，点M，N分别为OA，BC的中点.若，且G，M，N三点共线，则(   )A. B. C. D.9.如图，两块全等的直角边长为1的等腰直角三角形拼在一起，若，则(   )A.  B.C.2  D.10.如图，在中，BE是AC边上的中线，O是BE边的中点.若，则(   )A.  B.C.  D.11.设a，b为单位向量，且，则______.12.已知实数x，y，向量不共线，若，则____，_____.13.设D为所在平面内一点，.若，则______.14.已知向量.若向量与共线，则实数________.15.如图，在中，于点H.若，则___________.
答案以及解析1.答案：C解析：由知四边形ABCD为平行四边形，由知平行四边形ABCD为菱形.2.答案：C解析：因为，所以，所以点H是线段AD的中点，所以.故选C.3.答案：A解析：是以为邻边的平行四边形的对角线，且过AB的中点，设AB的中点为D，则.又D为AB的中点，C，O，D三点共线，为的重心.4.答案：A解析：如图，，故四边形ODFE为菱形，OF是的平分线.因为，所以点P在平分线所在直线上.5.答案：D解析：根据题意得，又，所以.故选D.6.答案：B解析：由向量的方向相反，得，，解得或(舍去)，则x的值是-2.7.答案：C解析：，.因为A，B，C三点共线，所以，所以，整理得，解得或.8.答案：B解析：若G，M，N三点共线，则存在实数使得成立，所以，即，所以，所以.故选B.9.答案：A解析：由题意知，.所以，则.10.答案：D解析：在中，BE是AC边上的中线，.是BE边的中点，，故选D.11.答案：解析：因为a，b为单位向量，且，所以，所以.又因为，所以.12.答案：；解析：由已知得解得13.答案：-3解析：为所在平面内一点，，三点共线.又，即，则，解得.14.答案：解析：因为，所以，故.15.答案：解析：，，，故，故.