高考数学真题专项练习 专题15 平面向量的概念、线性运算、平面向量基本定理（解析版）

专题15 平面向量的概念、线性运算、平面向量基本定理

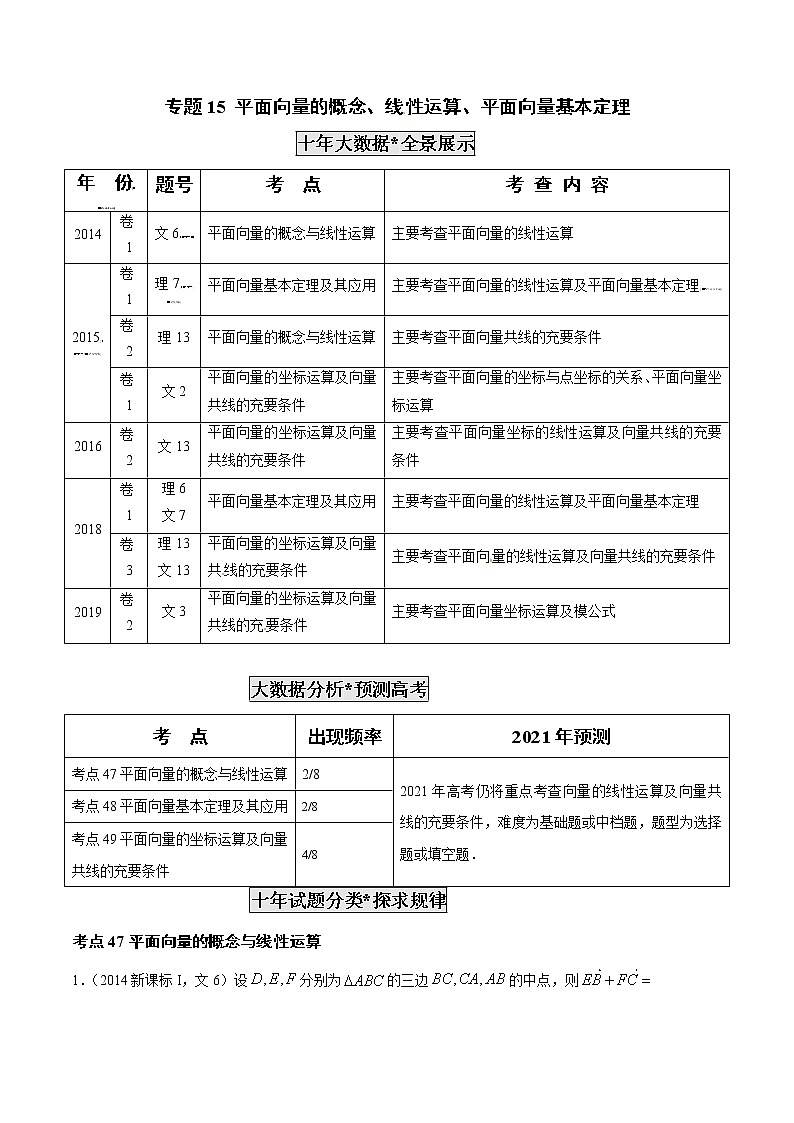
十年大数据*全景展示

大数据分析*预测高考

十年试题分类*探求规律

考点47平面向量的概念与线性运算

1．（2014新课标I，文6）设分别为的三边的中点，则

1.     B．       C．        D．

【答案】C

【解析】==，故选C．

2．（2014福建）在下列向量组中，可以把向量表示出来的是

A．      B． 

C．     D．

【答案】B

【解析】对于A，C，D，都有∥，所以只有B成立．

考点48平面向量基本定理及其应用

1．（2020江苏13）在中，，，，在边上，延长到，使得，若（为常数），则的长度是             ．

【答案】

【解析】由向量系数为常数，结合等和线性质可知，

故，，故，故．

在中，；在中，由正弦定理得，

即．

2．（2018•新课标Ⅰ，理6文7）在中，为边上的中线，为的中点，则　　

A． B． C． D．

【答案】A

【解析】在中，为边上的中线，为的中点，∴

，故选．

3．（2015新课标Ⅰ，理7）设D为ABC所在平面内一点，则（  ）

（A）  (B)

（C）   (D)

【答案】A

【解析】由题知=，故选A．

4．（2013广东）设是已知的平面向量且，关于向量的分解，有如下四个命题：

①给定向量，总存在向量，使；

②给定向量和，总存在实数和，使；

③给定单位向量和正数，总存在单位向量和实数，使；

④给定正数和，总存在单位向量和单位向量，使；

上述命题中的向量，和在同一平面内且两两不共线，则真命题的个数是

A．1 B．2         C．3         D．4

【答案】B

【解析】利用向量加法的三角形法则，易的①是对的；利用平面向量的基本定理，易的②是对的；以的终点作长度为的圆，这个圆必须和向量有交点，这个不一定能满足，③是错的；利用向量加法的三角形法则，结合三角形两边的和大于第三边，即必须，所以④是假命题．综上，本题选B．

5．（2017江苏）如图，在同一个平面内，向量，，的模分别为1，1，，与的夹角为，且，与的夹角为．若=+（，），则=         ．

【答案】3

【解析】由可得，，由=+得，即，两式相加得，，所以，所以．

6．（2013北京）向量a，b，c在正方形网格中的位置如图所示，若 (λ，μ∈R)，则=   ．

【答案】4

【解析】 如图建立坐标系，则，，．由，可得，∴

7．(2015北京)在中，点，满足，，若，则        ；       ．

【答案】 

【解析】由 =．所以，．

考点49平面向量的坐标运算及平面向量共线的充要条件

1．（2019•新课标Ⅱ，文3）已知向量，，则　　

A． B．2 C． D．50

【答案】A

【解析】，，，，，，，故选．

2．（2013辽宁）已知点，，则与向量同方向的单位向量为

A．     B．      C．     D．

【答案】A

【解析】，所以，这样同方向的单位向量是．

3．（2011广东）已知向量=（1，2），=（1，0），=（3，4）．若为实数， ，则=

 A．     B．     C．1   D．2

【答案】B

【解析】，由∥，得，解得

4．（2018•新课标Ⅲ，理13）已知向量，，．若，则　　．

【答案】

【解析】向量，，，，，

，解得．

5．(2016新课标，文13) 已知向量a=(m，4)，b=(3，−2)，且a∥b，则m=___________．  [来源：Z．xx．k．Com]

【答案】

【解析】因为a∥b，所以，解得．

6．（2015•新课标Ⅱ，理13）设向量，不平行，向量与平行，则实数　　．

【答案】

【解析】向量，不平行，向量与平行，，

，解得实数．

7．(2015江苏)已知向量，，若（R），

则 的值为___．

【答案】－3

【解析】由题意得：

8．(2014北京)已知向量、满足，，且()，则__．

【答案】

【解析】∵，∴可令，∵，∴，即，解得得．

9．（2014陕西）设，向量，，若，则

_______．

【答案】

【解析】∵，∴，∴，∵，∴．