安徽省阜阳市颍州区大田中学2022-2023学年八年级数学上学期期末模拟测试题 (含答案)

安徽省阜阳市颍州区大田中学2022-2023学年八年级数学上册期末模拟测试题（附答案）

一．选择题（满分30分）

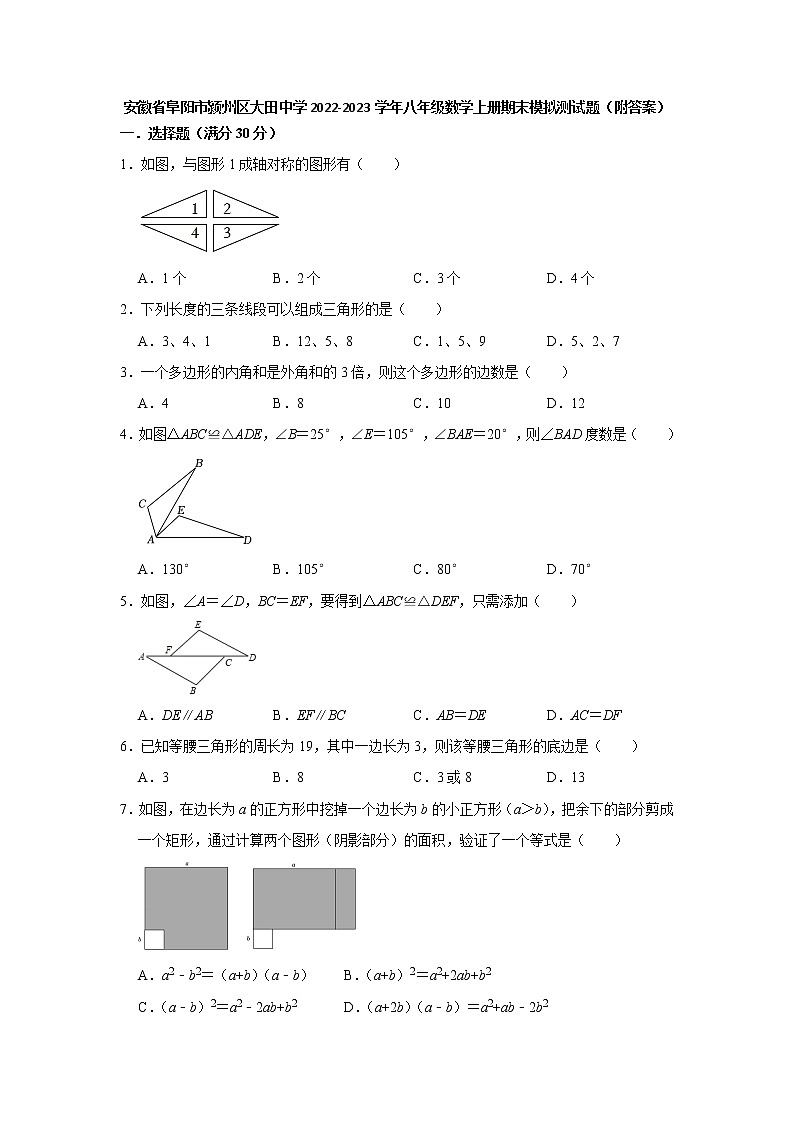
1．如图，与图形1成轴对称的图形有（　　）

A．1个 B．2个 C．3个 D．4个

2．下列长度的三条线段可以组成三角形的是（　　）

A．3、4、1 B．12、5、8 C．1、5、9 D．5、2、7

3．一个多边形的内角和是外角和的3倍，则这个多边形的边数是（　　）

A．4 B．8 C．10 D．12

4．如图△ABC≌△ADE，∠B＝25°，∠E＝105°，∠BAE＝20°，则∠BAD度数是（　　）

A．130° B．105° C．80° D．70°

5．如图，∠A＝∠D，BC＝EF，要得到△ABC≌△DEF，只需添加（　　）

A．DE∥AB B．EF∥BC C．AB＝DE D．AC＝DF

6．已知等腰三角形的周长为19，其中一边长为3，则该等腰三角形的底边是（　　）

A．3 B．8 C．3或8 D．13

7．如图，在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下的部分剪成一个矩形，通过计算两个图形（阴影部分）的面积，验证了一个等式是（　　）

A．a2﹣b2＝（a+b）（a﹣b）     B．（a+b）2＝a2+2ab+b2 

C．（a﹣b）2＝a2﹣2ab+b2     D．（a+2b）（a﹣b）＝a2+ab﹣2b2

8．下列从左到右的变形是因式分解的是（　　）

A．a2+a＝a（a+2） B．x2﹣4＝（x+4）（x﹣4） 

C．x3﹣x＝x（x+1）（x﹣1） D．x2+4x+1＝（x+2）2

9．若a≠b，则下列化简正确的是（　　）

A．＝ B．＝ C．＝ D．＝

10．在显微镜下测得一个病毒的直径为0.00000000205米，该数据用科学记数法表示为（　　）

A．0.205×10﹣8米 B．2.05×109米 

C．20.5×10﹣10米 D．2.05×10﹣9米

二．填空题（满分18分）

11．在△ABC中，若P为边BC延长线上的点，且∠A＝40°，∠B＝70°，则∠ACP的度数是　   　．

12．如图，在△ABC和△DEF中，∠A＝∠D＝90°，AB＝DF，若要用“斜边直角边（H．L．）”直接证明Rt△ABC≌Rt△DFE，则还需补充条件：　   　．

13．如图，∠BAC＝30°，P是∠BAC平分线上一点，PM∥AC，PD⊥AC，PD＝6，则△AMP的面积为 　   　．

14．（1）在有理数范围内分解因式：x4﹣7x2+1＝　   　．

（2）已知：x，y，z满足x+＝4，y+＝1，z+＝．则x＝　   　，y＝　   　，z＝　   　．

15．当x　   　时，分式有意义．

16．王小明腿有残疾，他的好朋友李阳非常关心他如图，李阳家到学校的路程是0.5km，到王小明家的路程是3km．李阳原来是步行上学．为让王小明每天准时到学校上课，他坚持骑小三轮车接送王小明，已知李阳骑小三轮车的速度是他步行速度的3倍，接送王小明上学要比他自己步行上学多用20min，求李阳步行速度和骑车速度各是多少？如果设李阳步行的速度为xkm/h，根据题意，可列方程为 　   　．

三．解答题（满分72分）

17．计算：

（1）x2•x5+x14÷x7．

（2）（﹣2x2y）2﹣2xy•（x3y）．

（3）|﹣3|+（﹣1）2020×（π﹣3）0﹣（﹣）﹣3．

（4）（﹣0.25）15×416．

18．分解因式：

①x2﹣6xy+9y2﹣1；

②（a+b）2+（a+b）（a﹣3b）．

19．解分式方程：

（1）；

（2）．

20．如图，点E是△ABC的边BC的延长线上的一点，证明：∠ACE＝∠A+∠B．

21．如图，AC与BD相交于点O，∠DBA＝∠CAB，∠1＝∠2．求证：∠CDA＝∠DCB．

22．如图，等边△ABC中，BD是边AC上的高，延长BC到点E，使CE＝CD，求证：BD＝DE．

23．如图1所示，边长为a的大正方形中有一个边长为b的小正方形，如图2是由图1中阴影部分拼成的一个长方形．

（1）请你分别表示出这两个图形中阴影部分的面积：　   　、　   　；

（2）请问以上结果可以验证哪个乘法公式？

（3）试利用这个公式计算：20222﹣2023×2021．

24．甲、乙两地相距1400km，从甲地到乙地乘高铁列车比乘特快列车少用9h，已知高铁列车的平均速度是特快列车的2.8倍．

（1）写出这一问题中的所有等量关系；

（2）如果设特快列车的平均速度为xkm，请列出关于x的方程；

（3）如果设小明同学乘高铁列车从甲地到乙地需yh，请列出关于y的方程．

参考答案

一．选择题（满分30分）

1．解：如图，与图形1成轴对称的图形有2和4共2个．

故选：B．

2．解：A、3+1＝4，不能构成三角形，故此选项不合题意；

B、5+8＞12，能构成三角形，故此选项符合题意；

C、5+1＜9，不能构成三角形，故此选项不合题意；

D、5+2＝7，不能构成三角形，故此选项不合题意．

故选：B．

3．解：设这个多边形是n边形，由题意得：

（n﹣2）×180°＝3×360°，

解得：n＝8，

故选：B．

4．解：∵△ABC≌△ADE，

∴∠D＝∠B＝25°，

∵∠E＝105°，

∴∠EAD＝180°﹣105°﹣25°＝50°，

∵∠BAE＝20°，

∴∠BAD＝∠EAB+∠EAD＝50°+20°＝70°，

故选：D．

5．解：A．∵DE∥AB，

∴∠A＝∠D，

由∠A＝∠D，BC＝EF不符合全等三角形的判定定理，不能推出△ABC≌△DEF，故本选项不符合题意；

B．∵EF∥BC，

∴∠EFC＝∠BCA，

∠A＝∠D，∠EFC＝∠BCA，BC＝EF，符合全等三角形的判定定理AAS，能推出△ABC≌△DEF，故本选项符合题意；

C．BC＝EF，AB＝DE，∠A＝∠D，不符合全等三角形的判定定理，能推出△ABC≌△DEF，故本选项不符合题意；

D．AC＝DF，BC＝EF，∠A＝∠D，不符合全等三角形的判定定理，不能推出△ABC≌△CDE，故本选项不符合题意；

故选：B．

6．解：（1）当3是腰长时，底边为19﹣3×2＝13，

此时3+3＝6＜13，不能组成三角形；

（2）当3是底边时，腰长为×（19﹣3）＝8，

此时3，8，8三边能够组成三角形．

所以等腰三角形的底边是3．

故选：A．

7．解：阴影部分的面积等于大正方形的面积减去小正方形的面积，为a2﹣b2，

也可以看作是长为（a+b），宽为（a﹣b）的长方形，为（a+b）（a﹣b），

∴a2﹣b2＝（a+b）（a﹣b）．

故选：A．

8．解：A．a2+a＝a（a+1），故本选项不符合题意；

B．x2﹣4＝（x+2）（x﹣2），故本选项不符合题意；

C．从左边到右边的变形属于因式分解，故本选项符合题意；

D．x2+4x+1≠（x+2）2，故本选项不符合题意；

故选：C．

9．解：A、≠，故A不符合题意；

B、≠，故B不符合题意；

C、≠，故C不符合题意；

D、＝，故D符合题意；

故选：D．

10．解：0.00000000205米，该数据用科学记数法表示为2.05×10﹣9米．

故选：D．

二．填空题（满分18分）

11．解：∵∠A＝40°，∠B＝70°，

∵∠ACP＝∠A+∠B＝40°+70°＝110°，

∴∠ACP＝110°，

故答案为：110°．

12．解：在Rt△ABC和Rt△DEF中，

，

∴Rt△ABC≌Rt△DEF（HL），

故答案为：BC＝EF．

13．解：过P点作PH⊥AB于H，如图，

∵AP平分∠BAC，

∴PH＝PD＝6，∠BAP＝∠CAP，

∵PM∥AC，

∴∠MPA＝∠CAP，∠HMP＝∠BAC＝30°，

∴∠MAP＝∠MPA，

∴MA＝MP，

在△PHM中，∵∠HMP＝30°，

∴MP＝2PH＝12，

∴MA＝MP＝12，

∴S△AMP＝×12×6＝36．

故答案为：36．

14．解：（1）x4﹣7x2+1＝（x4+2x2+1）﹣9x2

＝（x2+1）2﹣（3x）2

＝（x2+1+3x）（x2+1﹣3x）

故答案为：（x2+1+3x）（x2+1﹣3x）．

（2）x+＝4 ①，y+＝1②，z+＝③．

由①得，y＝④，

由③得，z＝﹣＝，即，＝⑤，

把④⑤代入②得，+＝1，

解得，x＝，代入①③得，

+＝4，z+＝，

解得，y＝，z＝，

故答案为：x＝，y＝，z＝．

15．解：当2x+3≠0时，分式有意义，

可得x≠．

故答案为：x≠．

16．解：设李阳步行速度为xkm/h，则骑车速度是3xkm/h，

根据题意可得：﹣＝，

即﹣＝，

故答案为：﹣＝．

三．解答题（满分72分）

17．解：（1）原式＝x7+x7＝2x7；

（2）原式＝4x4y2﹣2x4y2＝2x4y2；

（3）原式＝3+1×1+8＝3+1+8＝12；

（4）原式＝（﹣0.25）15×415×4＝（﹣0.25×4）15×4＝﹣1×4＝﹣4．

18．解：（1）原式＝（x﹣3y）2﹣1

＝（x﹣3y+1）（x﹣3y﹣1）；

（2）原式＝（a+b）（a+b+a﹣3b）

＝2（a+b）（a﹣b）．

19．解：（1）去分母得：2x+6＝3x，

解得：x＝6，

经检验x＝6是分式方程的解；

（2）去分母得：2﹣x﹣1＝0，

解得：x＝1，

经检验x＝1是增根，分式方程无解．

20．证明：在△ABC中，∠A+∠B+∠ACB＝180°，

∵∠ACE+∠ACB＝180°，

∴∠ACE＝∠A+∠B．

21．证明：如图所示：

在△ABD和△BAC中，

，

∴△ABD≌△BAC（AAS）

∴AD＝BC，BD＝AC，∠DAB＝∠CBA，

又∵∠DAB＝∠DAC+∠CAB，

∠CBA＝∠CBD+∠DBA，

∴∠DAC＝∠CBD，

在△DAC和△CBD中，

，

∴△DAC≌△CBD（SAS），

∴∠CDA＝∠DCB．

22．证明：∵等边△ABC中，BD是边AC上的高，

∴∠ABD＝∠CBD＝30°，∠ACB＝60°，

∵CE＝CD，

∴∠CDE＝∠CED＝30°，

∴∠DBC＝∠CED，

∴BD＝DE．

23．解：（1）∵大正方形的面积为a2，小正方形的面积为b2，

故图（1）阴影部分的面积为：a2﹣b2，图（2）阴影部分的面积为：（a+b）（a﹣b），

故答案为：a2﹣b2，（a+b）（a﹣b）；

（2）以上结果可以验证乘法公式：a2﹣b2＝（a+b）（a﹣b）；

（3）原式＝20222﹣（2022+1）（2022﹣1）

＝20222﹣（20222﹣1）

＝20222﹣20222+1

＝1．

24．解：（1）等量关系：①乘高铁列车＝甲地到乙地比乘特快列车﹣9；②高铁列车的平均行驶速度＝特快列车的平均速度×2.8；

（2）设特快列车的平均行驶速度为xkm/h，由题意得，

解得：x＝100，

经检验x＝100是原分式方程的解，2.8x＝280，

答：特快列车的平均行驶速度为100km/h，特高铁列车的平均行驶速度为280km/h，

∴关于x的方程为；

（3）设小明乘高铁列车从甲地到乙地需yh，由题意得，

解得：y＝5，

经检验y＝5是原分式方程的解，y+9＝14，

答：小明乘高铁列车从甲地到乙地需5h，小明乘高特快列车从甲地到乙地需14h，

∴关于y的方程为．