
还剩15页未读,
继续阅读
重庆市中考数学一轮复习-专题09 分式方程(讲义)
展开
2021年中考数学一轮专题复习
学案09 分式方程
中考命题说明
考点
课标要求
考查角度
1
分式方程的定义和相关概念
会解可化为一元一次方程的分式方程.
常以选择题、填空题、解答题的形式考查分式方程的定义和解法.
2
分式方程的实际应用
会解决分式方程的实际应用问题,能根据具体问题的实际意义,检验结果是否合理.
常以选择题、填空题的形式考查分式方程的列法,以列方程解应用题的形式考查解分式方程的基本思想和列方程解应用题的意识.
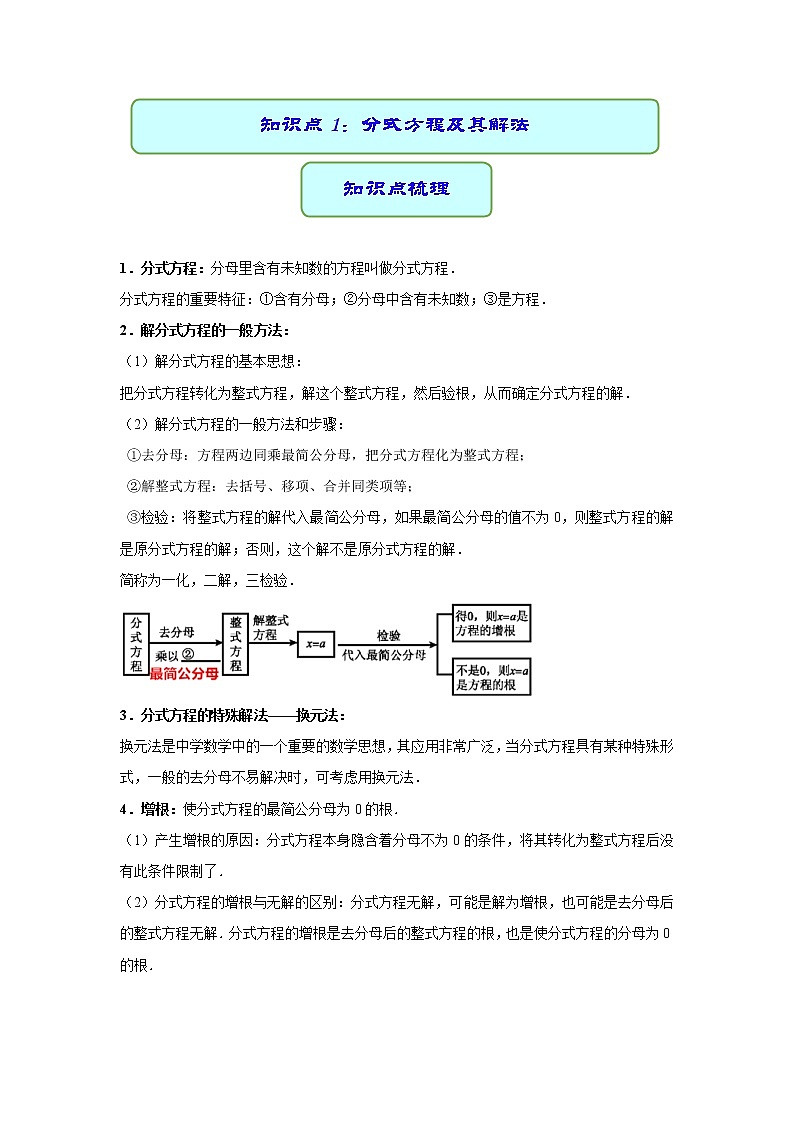
思维导图
知识点1:分式方程及其解法
知识点梳理
1.分式方程:分母里含有未知数的方程叫做分式方程.
分式方程的重要特征:①含有分母;②分母中含有未知数;③是方程.
2.解分式方程的一般方法:
(1)解分式方程的基本思想:
把分式方程转化为整式方程,解这个整式方程,然后验根,从而确定分式方程的解.
(2)解分式方程的一般方法和步骤:
①去分母:方程两边同乘最简公分母,把分式方程化为整式方程;
②解整式方程:去括号、移项、合并同类项等;
③检验:将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
简称为一化,二解,三检验.
3.分式方程的特殊解法——换元法:
换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法.
4.增根:使分式方程的最简公分母为0的根.
(1)产生增根的原因:分式方程本身隐含着分母不为0的条件,将其转化为整式方程后没有此条件限制了.
(2)分式方程的增根与无解的区别:分式方程无解,可能是解为增根,也可能是去分母后的整式方程无解.分式方程的增根是去分母后的整式方程的根,也是使分式方程的分母为0的根.
典型例题
【例1】下列各式中为分式方程的是( )
A. B. C. D.
【分析】根据分式方程的定义:分母里含有字母的方程叫做分式方程进行判断.
A、不是方程,故本选项错误;
B、方程的分母中含未知数x,所以它是分式方程.故本选项正确;
C、方程分母中不含未知数,所以它不是分式方程.故本选项错误;
D、方程的分母中不含未知数,所以它不是分式方程.故本选项错误;
故选B.
【答案】B.
【例2】若分式方程有增根,则这个增根是 .
【分析】根据分式方程有增根,让最简公分母为0确定增根,得到x-1=0,求出x的值即x=1.
【答案】x=1.
【例3】(2020•呼和浩特13/24)分式与的最简公分母是 ,方程的解是 .
【考点】解分式方程;最简公分母
【分析】根据最简公分母的定义得出结果,再解分式方程,检验,得解.
【解答】解:∵x2-2x=x(x-2),
∴分式与的最简公分母是x(x-2);
方程,
去分母得:2x2-8= x(x-2),
去括号得:2x2-8= x2-2x,
移项合并得:x2+2x-8=0,变形得:(x-2) (x+4)=0,
解得:x=2或x=-4,
∵当x=2时,x(x-2)=0,当x=-4时,x(x-2)≠0,
∴x=2是增根,
∴方程的解为:x=-4.
【点评】本题考查了最简公分母和解分式方程,解题的关键是掌握分式方程的解法.
知识点2:分式方程的应用
知识点梳理
1.分式方程实际应用的基本思路:
2.方法:一审:审清题意,弄清已知量和未知量;
二找:找出等量关系;
三设:设未知数;
四列:列出分式方程;
五解:解这个方程;
六验:检验,既要检验所求得的解是不是所列分式方程的解,又要检验所求得的解是否符合实际问题的要求(双检验);
七答:写出答案.
在上述过程中,关键步骤是根据题意寻找“等量关系”,进而列出分式方程,求解时注意必须检验求出的值是不是所列分式方程的解,且是否符合实际意义.
典型例题
【例4】(2020•兴安盟•呼伦贝尔9/26)甲、乙两人做某种机械零件,已知甲做240个零件与乙做280个零件所用的时间相等,两人每天共做130个零件.设甲每天做x个零件,下列方程正确的是( )
A. B.
C. D.
【考点】由实际问题抽象出分式方程
【分析】设甲每天做x个零件,根据甲做240个零件与乙做280个零件所用的时间相同,列出方程即可.
【解答】解:设甲每天做x个零件,根据题意得:
,
故选:A.
【点评】此题考查了由实际问题抽象出分式方程,找到关键描述语,找到等量关系是解决问题的关键.本题用到的等量关系为:工作时间=工作总量÷工作效率.
【例5】(2020•吉林17/26)甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.求乙每小时做零件的个数.
【考点】分式方程的应用
【分析】设乙每小时做x个零件,甲每小时做(x+6)个零件,根据时间=总工作量÷工作效率,即可得出关于x的分式方程,解之并检验后即可得出结论.
【解答】解:设乙每小时做x个零件,甲每小时做(x+6)个零件,
根据题意得:,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴x+6=18.
答:乙每小时做12个零件.
【点评】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
巩固训练
1.(2020•海南8/22)分式方程的解是
A. B. C. D.
2.(2020•包头14/26)分式方程=1的解是 .
3.(2020•重庆B卷10/26)若关于的一元一次不等式组的解集为,且关于的分式方程有非负整数解,则符合条件的所有整数的和为
A. B. C. D.0
4.(2020•重庆A卷10/26)若关于的一元一次不等式组的解集为;且关于的分式方程有正整数解,则所有满足条件的整数的值之积是( )
A.7 B. C.28 D.
5.(2020•上海2/25)用换元法解方程时,若设,则原方程可化为关于的方程是
A. B. C. D.
6.(2019·重庆市11/26)若关于x的一元一次不等式组的解集是x≤a,且关于y的分式方程﹣=1有非负整数解,则符合条件的所有整数a的和为( )
A.0 B.1 C.4 D.6
7.(2020•通辽18/26)解方程:.
8.(2020•陕西16/25)解分式方程:.
9.(2018·呼和浩特17(2)/25)解方程:+1=.
10.(2020•福建8/25)我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为株,则符合题意的方程是
A. B. C. D.
11.(2019•呼伦贝尔•兴安盟10/26)甲、乙两人分别从距目的地6千米和10千米的两地同时出发,乙的速度是甲的1.2倍,结果甲比乙早到20分钟.设甲的速度为千米时.根据题意,列方程正确的是
A. B. C. D.
12.(2018·通辽6/26)学校为创建“书香校园”,购买了一批图书.已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普书的数量比购买文学书的数量少100本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是x元,则可列方程为( )
A. B.
C. D.
13.(2018·巴彦淖尔7/24)小敏上月在某文具店正好用30元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小敏只比上次多用了6元钱,却比上次多买了8本,若设她上月买了x本笔记本,则根据题意可列方程为( )
A.﹣=1 B.﹣=1
C.﹣=1 D.﹣=1
14.甲、乙两辆汽车同时从A地出发,开往相距200 km的B地,甲、乙两车的速度之比是4∶5,结果乙车比甲车早30分钟到达B地,则甲车的速度为_________km/h.
15.(2020•赤峰22/26)甲、乙两支工程队修建二级公路,已知甲队每天修路的长度是乙队的2倍,如果两队各自修建公路500m,甲队比乙队少用5天.
(1)求甲,乙两支工程队每天各修路多少米?
(2)我市计划修建长度为3600m的二级公路,因工程需要,须由甲、乙两支工程队来完成.若甲队每天所需费用为1.2万元,乙队每天所需费用为0.5万元,求在总费用不超过40万元的情况下,至少安排乙队施工多少天?
16.(2020•广东23/25)某社区拟建,两类摊位以搞活“地摊经济”,每个类摊位的占地面积比每个类摊位的占地面积多2平方米.建类摊位每平方米的费用为40元,建类摊位每平方米的费用为30元.用60平方米建类摊位的个数恰好是用同样面积建类摊位个数的.
(1)求每个,类摊位占地面积各为多少平方米?
(2)该社区拟建,两类摊位共90个,且类摊位的数量不少于类摊位数量的3倍.求建造这90个摊位的最大费用.
17.(2018·兴安盟·呼伦贝尔19/26)一艘轮船在静水中的最大航速为,它以最大航速沿江顺流航行所用时间,与以最大航速逆流航行所用时间相等,江水的流速为多少?
18.(2018·包头23/26)某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
19.甲乙两人制作某种机械零件.已知甲每小时比乙多做3个,甲做96个所用时间与乙做84个所用时间相等,求甲乙两人每小时各做多少个零件?
巩固训练解析
1.(2020•海南8/22)分式方程的解是
A. B. C. D.
【考点】解分式方程
【分析】根据解分式方程的步骤进行计算即可.
【解答】解:去分母,得
,
移项合并同类项,得
.
检验:把代入,
所以原分式方程的解为:.
故选:C.
【点评】本题考查了解分式方程,解决本题的关键是掌握解分式方程的步骤.
2.(2020•包头14/26)分式方程=1的解是 .
【考点】解分式方程.
【答案】见试题解答内容
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:分式方程=1,
去分母得:3﹣x﹣x=x﹣2,
解得:x=,
经检验x=是分式方程的解.
故答案为:x=.
【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
3.(2020•重庆B卷10/26)若关于的一元一次不等式组的解集为,且关于的分式方程有非负整数解,则符合条件的所有整数的和为
A. B. C. D.0
【考点】一元一次不等式组的整数解;分式方程的解;解一元一次不等式组
【分析】不等式组整理后,根据已知解集确定出的范围,分式方程去分母转化为正整数方程,由分式方程有非负整数解,确定出的值,求出之和即可.
【解答】解:不等式组整理得:,
由解集为,得到,即,
分式方程去分母得:,即,
解得:,
由为非负整数,且,得到,,之和为,
故选:B.
【点评】此题考查了分式方程的解,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.
4.(2020•重庆A卷10/26)若关于的一元一次不等式组的解集为;且关于的分式方程有正整数解,则所有满足条件的整数的值之积是( )
A.7 B. C.28 D.
【考点】一元一次不等式组的整数解;分式方程的解;解一元一次不等式组
【分析】不等式组整理后,根据已知解集确定出的范围,分式方程去分母转化为正整数方程,由分式方程有非负整数解,确定出的值,求出之和即可.
【解答】解:不等式组整理得:,
由解集为,得到,
分式方程去分母得:,即,
解得:,
由为正整数解,且得到,7
,
故选:A.
【点评】此题考查了分式方程的解,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.
5.(2020•上海2/25)用换元法解方程时,若设,则原方程可化为关于的方程是
A. B. C. D.
【考点】换元法解分式方程
【分析】方程的两个分式具备倒数关系,设,则原方程化为,再转化为整式方程即可求解.
【解答】解:把代入原方程得:,转化为整式方程为.
故选:A.
【点评】考查了换元法解分式方程,换元法解分式方程时常用方法之一,它能够把一些分式方程化繁为简,化难为易,对此应注意总结能用换元法解的分式方程的特点,寻找解题技巧.
6.(2019·重庆市11/26)若关于x的一元一次不等式组的解集是x≤a,且关于y的分式方程﹣=1有非负整数解,则符合条件的所有整数a的和为( )
A.0 B.1 C.4 D.6
【考点】分式方程的解;解一元一次不等式组.
【分析】先解关于x的一元一次不等式组,再根据其解集是x≤a,得a小于5;再解分式方程,根据其有非负整数解,同时考虑增根的情况,得出a的值,再求和即可.
【解答】解:由不等式组得:
∵解集是x≤a,
∴a<5;
由关于y的分式方程﹣=1得2y﹣a+y﹣4=y﹣1
∴y=,
∵有非负整数解,
∴≥0,
∴5>a≥﹣3,
且a=﹣3,a=﹣1(舍,此时分式方程为增根),a=1,a=3
它们的和为1.
故选:B.
【点评】本题综合考查了含参一元一次不等式,含参分式方程得问题,需要考虑的因素较多,属于易错题.
7.(2020•通辽18/26)解方程:.
【考点】解分式方程
【分析】方程两边都乘以最简公分母把分式方程化为整式方程,然后解整式方程,再进行检验.
【解答】解:方程两边都乘以得,
,
解得,
检验:当时,,
所以是分式方程的解.
因此,原分式方程的解是.
【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
8.(2020•陕西16/25)解分式方程:.
【考点】解分式方程
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到的值,经检验即可得到分式方程的解.
【解答】解:方程,
去分母得:,
解得:,
经检验是分式方程的解.
【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
9.(2018·呼和浩特17(2)/25)解方程:+1=.
【考点】解分式方程.
【分析】根据解分式方程的步骤依次计算可得.
【解答】解:两边都乘以x﹣2,得:x﹣3+x﹣2=﹣3,
解得:x=1,
检验:x=1时,x﹣2=﹣1≠0,
所以分式方程的解为x=1.
【点评】本题主要考查实数的混合运算与解分式方程的能力,解题的关键是掌握解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.
10.(2020•福建8/25)我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为株,则符合题意的方程是
A. B. C. D.
【考点】由实际问题抽象出分式方程
【分析】根据单价总价数量结合少拿一株椽后剩下的椽的运费恰好等于一株椽的价钱,即可得出关于的分式方程,此题得解.
【解答】解:依题意,得:.
故选:A.
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
11.(2019•呼伦贝尔•兴安盟10/26)甲、乙两人分别从距目的地6千米和10千米的两地同时出发,乙的速度是甲的1.2倍,结果甲比乙早到20分钟.设甲的速度为千米时.根据题意,列方程正确的是
A. B. C. D.
【考点】由实际问题抽象出分式方程
【分析】设甲的速度为千米时,则乙的速度为千米时,根据时间路程速度结合甲比乙提前20分钟到达目的地,即可得出关于的分式方程,此题得解.
【解答】解:设甲的速度为千米时,则乙的速度为千米时,
根据题意得:.
故选:D.
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
12.(2018·通辽6/26)学校为创建“书香校园”,购买了一批图书.已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普书的数量比购买文学书的数量少100本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是x元,则可列方程为( )
A. B.
C. D.
【考点】由实际问题抽象出分式方程.
【分析】直接利用购买科普书的数量比购买文学书的数量少100本得出等式进而得出答案.
【解答】解:设科普类图书平均每本的价格是x元,则可列方程为:
.
故选:B.
【点评】此题主要考查了由实际问题抽象出分式方程,正确得出等量关系是解题关键.
13.(2018·巴彦淖尔7/24)小敏上月在某文具店正好用30元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小敏只比上次多用了6元钱,却比上次多买了8本,若设她上月买了x本笔记本,则根据题意可列方程为( )
A.﹣=1 B.﹣=1
C.﹣=1 D.﹣=1
【考点】由实际问题抽象出分式方程.
【分析】设她上月买了x本笔记本,则她本月买了(x+8)本笔记本,根据单价=总价÷数量结合每本比上月便宜1元,即可得出关于x的分式方程,此题得解.
【解答】解:设她上月买了x本笔记本,则她本月买了(x+8)本笔记本,
根据题意得:﹣=1.
故选:B.
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
14.甲、乙两辆汽车同时从A地出发,开往相距200 km的B地,甲、乙两车的速度之比是4∶5,结果乙车比甲车早30分钟到达B地,则甲车的速度为_________km/h.
【分析】设甲车的速度为x km/h,则乙车的速度为x km/h,
依题意,得:,解得:x=80,
经检验,x=80是原方程的解,且符合题意.故答案为:80.
【答案】80.
15.(2020•赤峰22/26)甲、乙两支工程队修建二级公路,已知甲队每天修路的长度是乙队的2倍,如果两队各自修建公路500m,甲队比乙队少用5天.
(1)求甲,乙两支工程队每天各修路多少米?
(2)我市计划修建长度为3600m的二级公路,因工程需要,须由甲、乙两支工程队来完成.若甲队每天所需费用为1.2万元,乙队每天所需费用为0.5万元,求在总费用不超过40万元的情况下,至少安排乙队施工多少天?
【考点】分式方程的应用;一元一次不等式的应用.有
【答案】(1)甲工程队每天修路100米,乙工程队每天修路50米;
(2)至少安排乙工程队施工32天.
【分析】(1)设乙工程队每天修路x米,则甲工程队每天修路2x米,根据工作时间=工作总量÷工作效率结合两队各自修建公路500m时甲队比乙队少用5天,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设安排乙工程队施工m天,则安排甲工程队施工(36﹣0.5m)天,根据总费用不超过40万元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.
【解答】解:(1)设乙工程队每天修路x米,则甲工程队每天修路2x米,
依题意,得: =5,
解得:x=50,
经检验,x=50是原方程的解,且符合题意,
∴2x=100.
答:甲工程队每天修路100米,乙工程队每天修路50米.
(2)设安排乙工程队施工m天,则安排甲工程队施工=(36﹣0.5m)天,
依题意,得:0.5m+1.2(36﹣0.5m)≤40,
解得:m≥32.
答:至少安排乙工程队施工32天.
【点评】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
16.(2020•广东23/25)某社区拟建,两类摊位以搞活“地摊经济”,每个类摊位的占地面积比每个类摊位的占地面积多2平方米.建类摊位每平方米的费用为40元,建类摊位每平方米的费用为30元.用60平方米建类摊位的个数恰好是用同样面积建类摊位个数的.
(1)求每个,类摊位占地面积各为多少平方米?
(2)该社区拟建,两类摊位共90个,且类摊位的数量不少于类摊位数量的3倍.求建造这90个摊位的最大费用.
【考点】分式方程的应用;一元一次不等式的应用
【分析】(1)设每个类摊位的占地面积为平方米,则每个类摊位占地面积为平方米,根据用60平方米建类摊位的个数恰好是用同样面积建类摊位个数的这个等量关系列出方程即可.
(2)设建摊位个,则建摊位个,结合“类摊位的数量不少于类摊位数量的3倍”列出不等式并解答.
【解答】解:(1)设每个类摊位的占地面积为平方米,则每个类摊位占地面积为平方米,
根据题意得:,
解得:,
经检验是原方程的解,
所以,
答:每个类摊位占地面积为5平方米,每个类摊位的占地面积为3平方米;
(2)设建摊位个,则建摊位个,
由题意得:,
解得,
建类摊位每平方米的费用为40元,建类摊位每平方米的费用为30元,
要想使建造这90个摊位有最大费用,所以要多建造类摊位,即取最大值22时,费用最大,
此时最大费用为:,
答:建造这90个摊位的最大费用是10520元.
【点评】本题考查了分式方程的应用和一元一次不等式的应用.解决本题的关键是读懂题意,找到符合题意的数量关系.
17.(2018·兴安盟·呼伦贝尔19/26)一艘轮船在静水中的最大航速为,它以最大航速沿江顺流航行所用时间,与以最大航速逆流航行所用时间相等,江水的流速为多少?
【考点】分式方程的应用
【分析】根据题意可得顺水速度为,逆水速度为,根据题意可得等量关系:以最大航速沿江顺流航行所用时间以最大航速逆流航行所用时间,根据等量关系列出方程求解即可.
【解答】解:设江水的流速为,
根据题意得:,
,
解得:.
经检验,是原方程的解.
答:江水的流速为.
【点评】此题主要考查了由实际问题抽象出分式方程,关键是正确理解题意,表示出顺水和逆水行驶速度,找出题目中等量关系,然后列出方程.
18.(2018·包头23/26)某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
【考点】一元一次方程的应用;分式方程的应用.
【分析】(1)设该商店3月份这种商品的售价为x元,则4月份这种商品的售价为0.9x元,根据数量=总价÷单价结合4月份比3月份多销售30件,即可得出关于x的分式方程,解之经检验即可得出结论;
(2)设该商品的进价为y元,根据销售利润=每件的利润×销售数量,即可得出关于y的一元一次方程,解之即可得出该商品的进价,再利用4月份的利润=每件的利润×销售数量,即可求出结论.
【解答】解:(1)设该商店3月份这种商品的售价为x元,则4月份这种商品的售价为0.9x元,
根据题意得:=﹣30,
解得:x=40,
经检验,x=40是原分式方程的解.
答:该商店3月份这种商品的售价是40元.
(2)设该商品的进价为y元,
根据题意得:(40﹣y)×=900,
解得:y=25,
∴(40×0.9﹣25)×=990(元).
答:该商店4月份销售这种商品的利润是990元.
【点评】本题考查了分式方程的应用以及一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找准等量关系,正确列出一元一次方程.
19.甲乙两人制作某种机械零件.已知甲每小时比乙多做3个,甲做96个所用时间与乙做84个所用时间相等,求甲乙两人每小时各做多少个零件?
【分析】设乙每小时做x个零件,则甲每小时做(x+3)个零件,根据等量关系:甲做96个所用时间与乙做84个所用时间相等,列出方程即可得解;
【答案】解:设乙每小时做x个零件,则甲每小时做(x+3)个零件,由题意得:
解得:x=21,
学案09 分式方程
中考命题说明
考点
课标要求
考查角度
1
分式方程的定义和相关概念
会解可化为一元一次方程的分式方程.
常以选择题、填空题、解答题的形式考查分式方程的定义和解法.
2
分式方程的实际应用
会解决分式方程的实际应用问题,能根据具体问题的实际意义,检验结果是否合理.
常以选择题、填空题的形式考查分式方程的列法,以列方程解应用题的形式考查解分式方程的基本思想和列方程解应用题的意识.
思维导图
知识点1:分式方程及其解法
知识点梳理
1.分式方程:分母里含有未知数的方程叫做分式方程.
分式方程的重要特征:①含有分母;②分母中含有未知数;③是方程.
2.解分式方程的一般方法:
(1)解分式方程的基本思想:
把分式方程转化为整式方程,解这个整式方程,然后验根,从而确定分式方程的解.
(2)解分式方程的一般方法和步骤:
①去分母:方程两边同乘最简公分母,把分式方程化为整式方程;
②解整式方程:去括号、移项、合并同类项等;
③检验:将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
简称为一化,二解,三检验.
3.分式方程的特殊解法——换元法:
换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法.
4.增根:使分式方程的最简公分母为0的根.
(1)产生增根的原因:分式方程本身隐含着分母不为0的条件,将其转化为整式方程后没有此条件限制了.
(2)分式方程的增根与无解的区别:分式方程无解,可能是解为增根,也可能是去分母后的整式方程无解.分式方程的增根是去分母后的整式方程的根,也是使分式方程的分母为0的根.
典型例题
【例1】下列各式中为分式方程的是( )
A. B. C. D.
【分析】根据分式方程的定义:分母里含有字母的方程叫做分式方程进行判断.
A、不是方程,故本选项错误;
B、方程的分母中含未知数x,所以它是分式方程.故本选项正确;
C、方程分母中不含未知数,所以它不是分式方程.故本选项错误;
D、方程的分母中不含未知数,所以它不是分式方程.故本选项错误;
故选B.
【答案】B.
【例2】若分式方程有增根,则这个增根是 .
【分析】根据分式方程有增根,让最简公分母为0确定增根,得到x-1=0,求出x的值即x=1.
【答案】x=1.
【例3】(2020•呼和浩特13/24)分式与的最简公分母是 ,方程的解是 .
【考点】解分式方程;最简公分母
【分析】根据最简公分母的定义得出结果,再解分式方程,检验,得解.
【解答】解:∵x2-2x=x(x-2),
∴分式与的最简公分母是x(x-2);
方程,
去分母得:2x2-8= x(x-2),
去括号得:2x2-8= x2-2x,
移项合并得:x2+2x-8=0,变形得:(x-2) (x+4)=0,
解得:x=2或x=-4,
∵当x=2时,x(x-2)=0,当x=-4时,x(x-2)≠0,
∴x=2是增根,
∴方程的解为:x=-4.
【点评】本题考查了最简公分母和解分式方程,解题的关键是掌握分式方程的解法.
知识点2:分式方程的应用
知识点梳理
1.分式方程实际应用的基本思路:
2.方法:一审:审清题意,弄清已知量和未知量;
二找:找出等量关系;
三设:设未知数;
四列:列出分式方程;
五解:解这个方程;
六验:检验,既要检验所求得的解是不是所列分式方程的解,又要检验所求得的解是否符合实际问题的要求(双检验);
七答:写出答案.
在上述过程中,关键步骤是根据题意寻找“等量关系”,进而列出分式方程,求解时注意必须检验求出的值是不是所列分式方程的解,且是否符合实际意义.
典型例题
【例4】(2020•兴安盟•呼伦贝尔9/26)甲、乙两人做某种机械零件,已知甲做240个零件与乙做280个零件所用的时间相等,两人每天共做130个零件.设甲每天做x个零件,下列方程正确的是( )
A. B.
C. D.
【考点】由实际问题抽象出分式方程
【分析】设甲每天做x个零件,根据甲做240个零件与乙做280个零件所用的时间相同,列出方程即可.
【解答】解:设甲每天做x个零件,根据题意得:
,
故选:A.
【点评】此题考查了由实际问题抽象出分式方程,找到关键描述语,找到等量关系是解决问题的关键.本题用到的等量关系为:工作时间=工作总量÷工作效率.
【例5】(2020•吉林17/26)甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.求乙每小时做零件的个数.
【考点】分式方程的应用
【分析】设乙每小时做x个零件,甲每小时做(x+6)个零件,根据时间=总工作量÷工作效率,即可得出关于x的分式方程,解之并检验后即可得出结论.
【解答】解:设乙每小时做x个零件,甲每小时做(x+6)个零件,
根据题意得:,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴x+6=18.
答:乙每小时做12个零件.
【点评】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
巩固训练
1.(2020•海南8/22)分式方程的解是
A. B. C. D.
2.(2020•包头14/26)分式方程=1的解是 .
3.(2020•重庆B卷10/26)若关于的一元一次不等式组的解集为,且关于的分式方程有非负整数解,则符合条件的所有整数的和为
A. B. C. D.0
4.(2020•重庆A卷10/26)若关于的一元一次不等式组的解集为;且关于的分式方程有正整数解,则所有满足条件的整数的值之积是( )
A.7 B. C.28 D.
5.(2020•上海2/25)用换元法解方程时,若设,则原方程可化为关于的方程是
A. B. C. D.
6.(2019·重庆市11/26)若关于x的一元一次不等式组的解集是x≤a,且关于y的分式方程﹣=1有非负整数解,则符合条件的所有整数a的和为( )
A.0 B.1 C.4 D.6
7.(2020•通辽18/26)解方程:.
8.(2020•陕西16/25)解分式方程:.
9.(2018·呼和浩特17(2)/25)解方程:+1=.
10.(2020•福建8/25)我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为株,则符合题意的方程是
A. B. C. D.
11.(2019•呼伦贝尔•兴安盟10/26)甲、乙两人分别从距目的地6千米和10千米的两地同时出发,乙的速度是甲的1.2倍,结果甲比乙早到20分钟.设甲的速度为千米时.根据题意,列方程正确的是
A. B. C. D.
12.(2018·通辽6/26)学校为创建“书香校园”,购买了一批图书.已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普书的数量比购买文学书的数量少100本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是x元,则可列方程为( )
A. B.
C. D.
13.(2018·巴彦淖尔7/24)小敏上月在某文具店正好用30元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小敏只比上次多用了6元钱,却比上次多买了8本,若设她上月买了x本笔记本,则根据题意可列方程为( )
A.﹣=1 B.﹣=1
C.﹣=1 D.﹣=1
14.甲、乙两辆汽车同时从A地出发,开往相距200 km的B地,甲、乙两车的速度之比是4∶5,结果乙车比甲车早30分钟到达B地,则甲车的速度为_________km/h.
15.(2020•赤峰22/26)甲、乙两支工程队修建二级公路,已知甲队每天修路的长度是乙队的2倍,如果两队各自修建公路500m,甲队比乙队少用5天.
(1)求甲,乙两支工程队每天各修路多少米?
(2)我市计划修建长度为3600m的二级公路,因工程需要,须由甲、乙两支工程队来完成.若甲队每天所需费用为1.2万元,乙队每天所需费用为0.5万元,求在总费用不超过40万元的情况下,至少安排乙队施工多少天?
16.(2020•广东23/25)某社区拟建,两类摊位以搞活“地摊经济”,每个类摊位的占地面积比每个类摊位的占地面积多2平方米.建类摊位每平方米的费用为40元,建类摊位每平方米的费用为30元.用60平方米建类摊位的个数恰好是用同样面积建类摊位个数的.
(1)求每个,类摊位占地面积各为多少平方米?
(2)该社区拟建,两类摊位共90个,且类摊位的数量不少于类摊位数量的3倍.求建造这90个摊位的最大费用.
17.(2018·兴安盟·呼伦贝尔19/26)一艘轮船在静水中的最大航速为,它以最大航速沿江顺流航行所用时间,与以最大航速逆流航行所用时间相等,江水的流速为多少?
18.(2018·包头23/26)某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
19.甲乙两人制作某种机械零件.已知甲每小时比乙多做3个,甲做96个所用时间与乙做84个所用时间相等,求甲乙两人每小时各做多少个零件?
巩固训练解析
1.(2020•海南8/22)分式方程的解是
A. B. C. D.
【考点】解分式方程
【分析】根据解分式方程的步骤进行计算即可.
【解答】解:去分母,得
,
移项合并同类项,得
.
检验:把代入,
所以原分式方程的解为:.
故选:C.
【点评】本题考查了解分式方程,解决本题的关键是掌握解分式方程的步骤.
2.(2020•包头14/26)分式方程=1的解是 .
【考点】解分式方程.
【答案】见试题解答内容
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
【解答】解:分式方程=1,
去分母得:3﹣x﹣x=x﹣2,
解得:x=,
经检验x=是分式方程的解.
故答案为:x=.
【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
3.(2020•重庆B卷10/26)若关于的一元一次不等式组的解集为,且关于的分式方程有非负整数解,则符合条件的所有整数的和为
A. B. C. D.0
【考点】一元一次不等式组的整数解;分式方程的解;解一元一次不等式组
【分析】不等式组整理后,根据已知解集确定出的范围,分式方程去分母转化为正整数方程,由分式方程有非负整数解,确定出的值,求出之和即可.
【解答】解:不等式组整理得:,
由解集为,得到,即,
分式方程去分母得:,即,
解得:,
由为非负整数,且,得到,,之和为,
故选:B.
【点评】此题考查了分式方程的解,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.
4.(2020•重庆A卷10/26)若关于的一元一次不等式组的解集为;且关于的分式方程有正整数解,则所有满足条件的整数的值之积是( )
A.7 B. C.28 D.
【考点】一元一次不等式组的整数解;分式方程的解;解一元一次不等式组
【分析】不等式组整理后,根据已知解集确定出的范围,分式方程去分母转化为正整数方程,由分式方程有非负整数解,确定出的值,求出之和即可.
【解答】解:不等式组整理得:,
由解集为,得到,
分式方程去分母得:,即,
解得:,
由为正整数解,且得到,7
,
故选:A.
【点评】此题考查了分式方程的解,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.
5.(2020•上海2/25)用换元法解方程时,若设,则原方程可化为关于的方程是
A. B. C. D.
【考点】换元法解分式方程
【分析】方程的两个分式具备倒数关系,设,则原方程化为,再转化为整式方程即可求解.
【解答】解:把代入原方程得:,转化为整式方程为.
故选:A.
【点评】考查了换元法解分式方程,换元法解分式方程时常用方法之一,它能够把一些分式方程化繁为简,化难为易,对此应注意总结能用换元法解的分式方程的特点,寻找解题技巧.
6.(2019·重庆市11/26)若关于x的一元一次不等式组的解集是x≤a,且关于y的分式方程﹣=1有非负整数解,则符合条件的所有整数a的和为( )
A.0 B.1 C.4 D.6
【考点】分式方程的解;解一元一次不等式组.
【分析】先解关于x的一元一次不等式组,再根据其解集是x≤a,得a小于5;再解分式方程,根据其有非负整数解,同时考虑增根的情况,得出a的值,再求和即可.
【解答】解:由不等式组得:
∵解集是x≤a,
∴a<5;
由关于y的分式方程﹣=1得2y﹣a+y﹣4=y﹣1
∴y=,
∵有非负整数解,
∴≥0,
∴5>a≥﹣3,
且a=﹣3,a=﹣1(舍,此时分式方程为增根),a=1,a=3
它们的和为1.
故选:B.
【点评】本题综合考查了含参一元一次不等式,含参分式方程得问题,需要考虑的因素较多,属于易错题.
7.(2020•通辽18/26)解方程:.
【考点】解分式方程
【分析】方程两边都乘以最简公分母把分式方程化为整式方程,然后解整式方程,再进行检验.
【解答】解:方程两边都乘以得,
,
解得,
检验:当时,,
所以是分式方程的解.
因此,原分式方程的解是.
【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
8.(2020•陕西16/25)解分式方程:.
【考点】解分式方程
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到的值,经检验即可得到分式方程的解.
【解答】解:方程,
去分母得:,
解得:,
经检验是分式方程的解.
【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
9.(2018·呼和浩特17(2)/25)解方程:+1=.
【考点】解分式方程.
【分析】根据解分式方程的步骤依次计算可得.
【解答】解:两边都乘以x﹣2,得:x﹣3+x﹣2=﹣3,
解得:x=1,
检验:x=1时,x﹣2=﹣1≠0,
所以分式方程的解为x=1.
【点评】本题主要考查实数的混合运算与解分式方程的能力,解题的关键是掌握解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.
10.(2020•福建8/25)我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为株,则符合题意的方程是
A. B. C. D.
【考点】由实际问题抽象出分式方程
【分析】根据单价总价数量结合少拿一株椽后剩下的椽的运费恰好等于一株椽的价钱,即可得出关于的分式方程,此题得解.
【解答】解:依题意,得:.
故选:A.
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
11.(2019•呼伦贝尔•兴安盟10/26)甲、乙两人分别从距目的地6千米和10千米的两地同时出发,乙的速度是甲的1.2倍,结果甲比乙早到20分钟.设甲的速度为千米时.根据题意,列方程正确的是
A. B. C. D.
【考点】由实际问题抽象出分式方程
【分析】设甲的速度为千米时,则乙的速度为千米时,根据时间路程速度结合甲比乙提前20分钟到达目的地,即可得出关于的分式方程,此题得解.
【解答】解:设甲的速度为千米时,则乙的速度为千米时,
根据题意得:.
故选:D.
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
12.(2018·通辽6/26)学校为创建“书香校园”,购买了一批图书.已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普书的数量比购买文学书的数量少100本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是x元,则可列方程为( )
A. B.
C. D.
【考点】由实际问题抽象出分式方程.
【分析】直接利用购买科普书的数量比购买文学书的数量少100本得出等式进而得出答案.
【解答】解:设科普类图书平均每本的价格是x元,则可列方程为:
.
故选:B.
【点评】此题主要考查了由实际问题抽象出分式方程,正确得出等量关系是解题关键.
13.(2018·巴彦淖尔7/24)小敏上月在某文具店正好用30元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小敏只比上次多用了6元钱,却比上次多买了8本,若设她上月买了x本笔记本,则根据题意可列方程为( )
A.﹣=1 B.﹣=1
C.﹣=1 D.﹣=1
【考点】由实际问题抽象出分式方程.
【分析】设她上月买了x本笔记本,则她本月买了(x+8)本笔记本,根据单价=总价÷数量结合每本比上月便宜1元,即可得出关于x的分式方程,此题得解.
【解答】解:设她上月买了x本笔记本,则她本月买了(x+8)本笔记本,
根据题意得:﹣=1.
故选:B.
【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
14.甲、乙两辆汽车同时从A地出发,开往相距200 km的B地,甲、乙两车的速度之比是4∶5,结果乙车比甲车早30分钟到达B地,则甲车的速度为_________km/h.
【分析】设甲车的速度为x km/h,则乙车的速度为x km/h,
依题意,得:,解得:x=80,
经检验,x=80是原方程的解,且符合题意.故答案为:80.
【答案】80.
15.(2020•赤峰22/26)甲、乙两支工程队修建二级公路,已知甲队每天修路的长度是乙队的2倍,如果两队各自修建公路500m,甲队比乙队少用5天.
(1)求甲,乙两支工程队每天各修路多少米?
(2)我市计划修建长度为3600m的二级公路,因工程需要,须由甲、乙两支工程队来完成.若甲队每天所需费用为1.2万元,乙队每天所需费用为0.5万元,求在总费用不超过40万元的情况下,至少安排乙队施工多少天?
【考点】分式方程的应用;一元一次不等式的应用.有
【答案】(1)甲工程队每天修路100米,乙工程队每天修路50米;
(2)至少安排乙工程队施工32天.
【分析】(1)设乙工程队每天修路x米,则甲工程队每天修路2x米,根据工作时间=工作总量÷工作效率结合两队各自修建公路500m时甲队比乙队少用5天,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设安排乙工程队施工m天,则安排甲工程队施工(36﹣0.5m)天,根据总费用不超过40万元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.
【解答】解:(1)设乙工程队每天修路x米,则甲工程队每天修路2x米,
依题意,得: =5,
解得:x=50,
经检验,x=50是原方程的解,且符合题意,
∴2x=100.
答:甲工程队每天修路100米,乙工程队每天修路50米.
(2)设安排乙工程队施工m天,则安排甲工程队施工=(36﹣0.5m)天,
依题意,得:0.5m+1.2(36﹣0.5m)≤40,
解得:m≥32.
答:至少安排乙工程队施工32天.
【点评】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
16.(2020•广东23/25)某社区拟建,两类摊位以搞活“地摊经济”,每个类摊位的占地面积比每个类摊位的占地面积多2平方米.建类摊位每平方米的费用为40元,建类摊位每平方米的费用为30元.用60平方米建类摊位的个数恰好是用同样面积建类摊位个数的.
(1)求每个,类摊位占地面积各为多少平方米?
(2)该社区拟建,两类摊位共90个,且类摊位的数量不少于类摊位数量的3倍.求建造这90个摊位的最大费用.
【考点】分式方程的应用;一元一次不等式的应用
【分析】(1)设每个类摊位的占地面积为平方米,则每个类摊位占地面积为平方米,根据用60平方米建类摊位的个数恰好是用同样面积建类摊位个数的这个等量关系列出方程即可.
(2)设建摊位个,则建摊位个,结合“类摊位的数量不少于类摊位数量的3倍”列出不等式并解答.
【解答】解:(1)设每个类摊位的占地面积为平方米,则每个类摊位占地面积为平方米,
根据题意得:,
解得:,
经检验是原方程的解,
所以,
答:每个类摊位占地面积为5平方米,每个类摊位的占地面积为3平方米;
(2)设建摊位个,则建摊位个,
由题意得:,
解得,
建类摊位每平方米的费用为40元,建类摊位每平方米的费用为30元,
要想使建造这90个摊位有最大费用,所以要多建造类摊位,即取最大值22时,费用最大,
此时最大费用为:,
答:建造这90个摊位的最大费用是10520元.
【点评】本题考查了分式方程的应用和一元一次不等式的应用.解决本题的关键是读懂题意,找到符合题意的数量关系.
17.(2018·兴安盟·呼伦贝尔19/26)一艘轮船在静水中的最大航速为,它以最大航速沿江顺流航行所用时间,与以最大航速逆流航行所用时间相等,江水的流速为多少?
【考点】分式方程的应用
【分析】根据题意可得顺水速度为,逆水速度为,根据题意可得等量关系:以最大航速沿江顺流航行所用时间以最大航速逆流航行所用时间,根据等量关系列出方程求解即可.
【解答】解:设江水的流速为,
根据题意得:,
,
解得:.
经检验,是原方程的解.
答:江水的流速为.
【点评】此题主要考查了由实际问题抽象出分式方程,关键是正确理解题意,表示出顺水和逆水行驶速度,找出题目中等量关系,然后列出方程.
18.(2018·包头23/26)某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
【考点】一元一次方程的应用;分式方程的应用.
【分析】(1)设该商店3月份这种商品的售价为x元,则4月份这种商品的售价为0.9x元,根据数量=总价÷单价结合4月份比3月份多销售30件,即可得出关于x的分式方程,解之经检验即可得出结论;
(2)设该商品的进价为y元,根据销售利润=每件的利润×销售数量,即可得出关于y的一元一次方程,解之即可得出该商品的进价,再利用4月份的利润=每件的利润×销售数量,即可求出结论.
【解答】解:(1)设该商店3月份这种商品的售价为x元,则4月份这种商品的售价为0.9x元,
根据题意得:=﹣30,
解得:x=40,
经检验,x=40是原分式方程的解.
答:该商店3月份这种商品的售价是40元.
(2)设该商品的进价为y元,
根据题意得:(40﹣y)×=900,
解得:y=25,
∴(40×0.9﹣25)×=990(元).
答:该商店4月份销售这种商品的利润是990元.
【点评】本题考查了分式方程的应用以及一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)找准等量关系,正确列出一元一次方程.
19.甲乙两人制作某种机械零件.已知甲每小时比乙多做3个,甲做96个所用时间与乙做84个所用时间相等,求甲乙两人每小时各做多少个零件?
【分析】设乙每小时做x个零件,则甲每小时做(x+3)个零件,根据等量关系:甲做96个所用时间与乙做84个所用时间相等,列出方程即可得解;
【答案】解:设乙每小时做x个零件,则甲每小时做(x+3)个零件,由题意得:
解得:x=21,
相关资料
更多








