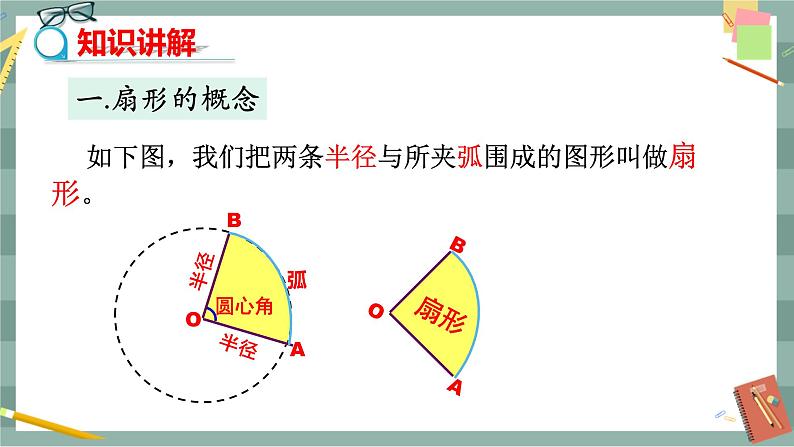
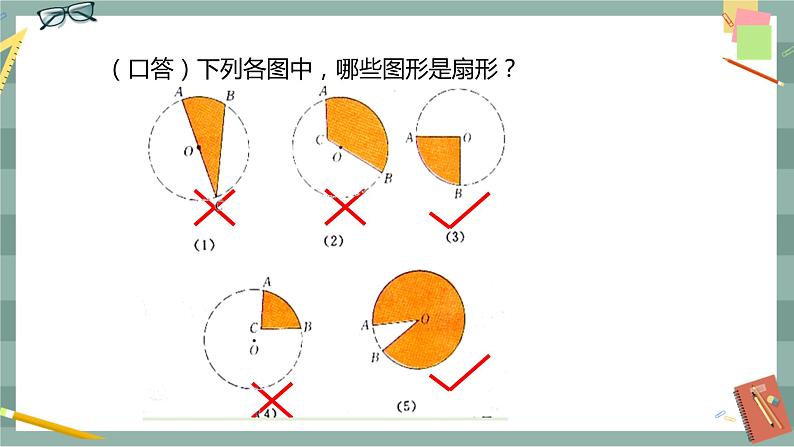
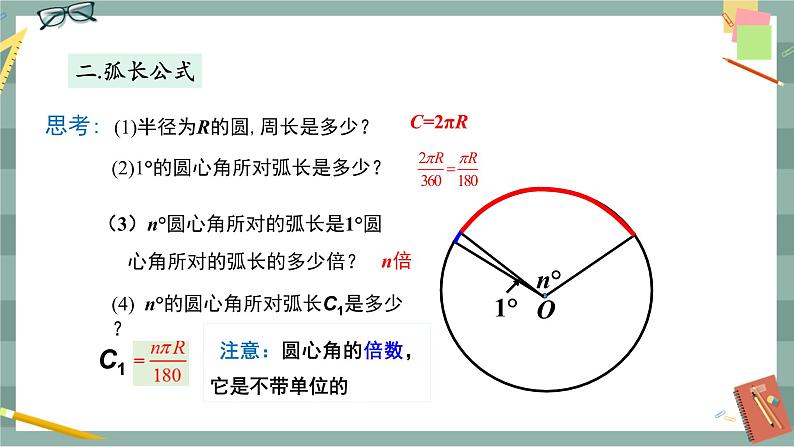
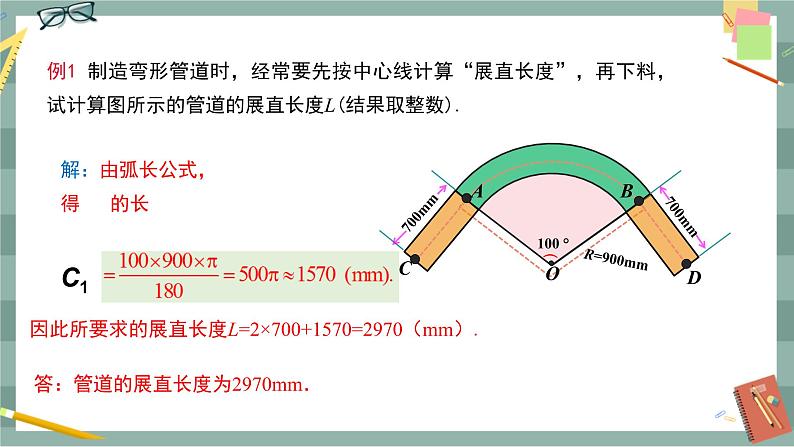
初中沪科版第24章 圆24.6 正多边形与圆24.6.2 正多边形的性质精品课件ppt

教学目标

1.进一步理解正多边形的概念，掌握正多边形的性质.

2.理解正多边形的中心、半径、边心距、 中心角等概念.

3.会运用正多边形的性质解决简单的实际问题.

教学重难点

重点：理解并掌握正多边形的半径和边长、边心距、中心角之间的关系.

难点：会应用正多边形和圆的有关知识解决实际问题.

教学过程

复习巩固

正多边形的性质：每条边都相等，每个角都相等.

正n边形的内角和：(n-2)·180°.

导入新课

问题：上节课我们学习了正多边形的定义，并且知道只要n等分(n≥3)圆周就可以得到圆的内接正n边形和圆的外切正n边形．反过来，是否每一个正多边形都有一个外接圆和内切圆呢？

探究新知

1.正多边形的性质

以正五边形为例：

过正五边形ABCDE的顶点A，B，C作⊙O，连接OA，OB，OC，OD.

∵ OB＝OC，

∴ ∠1＝∠2.

∵ ∠ABC＝∠BCD，

∴ ∠3＝∠4.

∵ AB＝DC，

∴ △AOB≌△DOC，

∴ OA＝OD，

即点D在⊙O上.同理，点E在⊙O上.

   ∵ 正五边形ABCDE的各边是⊙O中相等的弦，

∴ 弦心距相等．

因此，以点O为圆心，以弦心距(OH)为半径的圆与正五边形的各边都相切．可见正五边形ABCDE有一个以O为圆心的内切圆.

【归纳总结】任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆，如图所示.

2.正多边形的有关概念

3.正多边形的有关计算

例1　如图，已知半径为4的圆内接正六边形ABCDEF.

①它的中心角等于       度 .

②OC       BC（填>、<或＝）.

③△OBC是        三角形.

④圆内接正六边形的面积是△OBC面积的      倍.

⑤圆内接正n边形面积公式:________________________.

师生活动：引导学生思考，正多边形的中心角怎么计算？边长a、半径R、边心距r有什么关系？正多边形的面积如何计算？

【解】①60　② ＝  ③等边  ④6 

⑤

4.正多边形的对称性

问题：正三角形、正方形、正五边形、正六边形、…、正n边形都是轴对称图形吗？都是中心对称图形吗？

师生活动：学生尝试画以上图形的对称轴，教师适时点拨.

【归纳总结】1.正n边形都是轴对称图形，都有n条对称轴，只有边数为偶数的正多边形才是中心对称图形.

2.正n边形的每个内角都等于.

3.正n边形的每个中心角都等于.

【新知应用】

例2　如图，公园里有一个亭子，它的地基是半径为4 m的正六边形，求地基的周长和面积 (精确到0.1 m2).

师生活动：引导学生将实际问题转化成数学问题，将多边形转化成三角形来解决.

【解】如图，连接OB，OC.因为六边形ABCDEF是正六边形，所以它的中心角等于60º，所以△OBC是等边三角形，从而正六边形的边长等于它的半径.

因此，亭子地基的周长l＝6×4＝24（m）.

过点O作OP⊥BC，垂足为P.

在Rt△OPC中，OC＝4 m，PC＝，

利用勾股定理，可得边心距（m），

亭子地基的面积.

【归纳总结】将正多边形的中心、半径、中心角、边心距等一些量集中到一个三角形中来研究，可以利用勾股定理进行计算，进而能够求得正多边形的周长和面积.

课堂小结

布置作业

教材第52页第4，5，6，7题

板书设计

24.6　正多边形与圆

第2课时　正多边形的性质

1.正多边形的性质

2.正多边形的有关概念

3.正多边形的有关计算