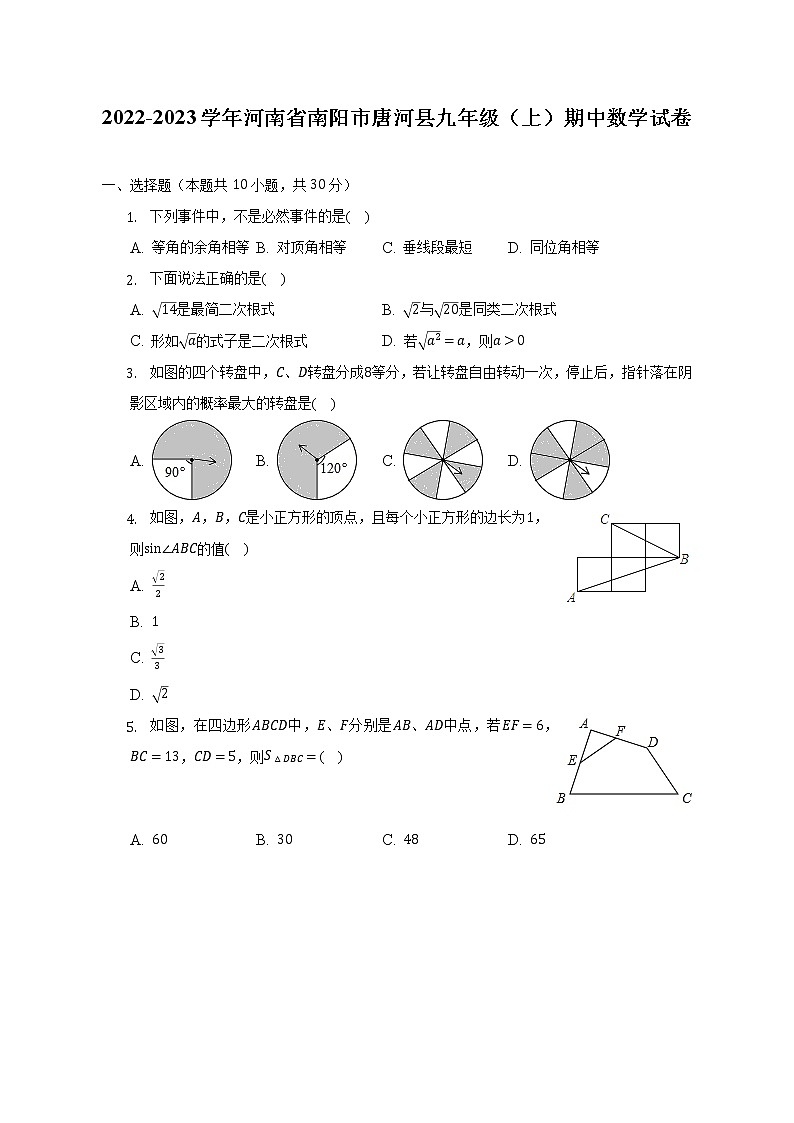
2022-2023学年河南省南阳市唐河县九年级（上）期中数学试卷(解析版)

2022-2023学年河南省南阳市唐河县九年级（上）期中数学试卷

一、选择题（本题共10小题，共30分）

1.    下列事件中，不是必然事件的是(    )

A. 等角的余角相等 B. 对顶角相等 C. 垂线段最短 D. 同位角相等

2.    下面说法正确的是(    )

A. 是最简二次根式 B. 与是同类二次根式
C. 形如的式子是二次根式 D. 若，则

3.    如图的四个转盘中，、转盘分成等分，若让转盘自由转动一次，停止后，指针落在阴影区域内的概率最大的转盘是(    )

A.  B.  C.  D.

4.    如图，，，是小正方形的顶点，且每个小正方形的边长为，则的值(    )

A.
B.
C.
D.

5.    如图，在四边形中，、分别是、中点，若，，，则(    )

A.  B.  C.  D.

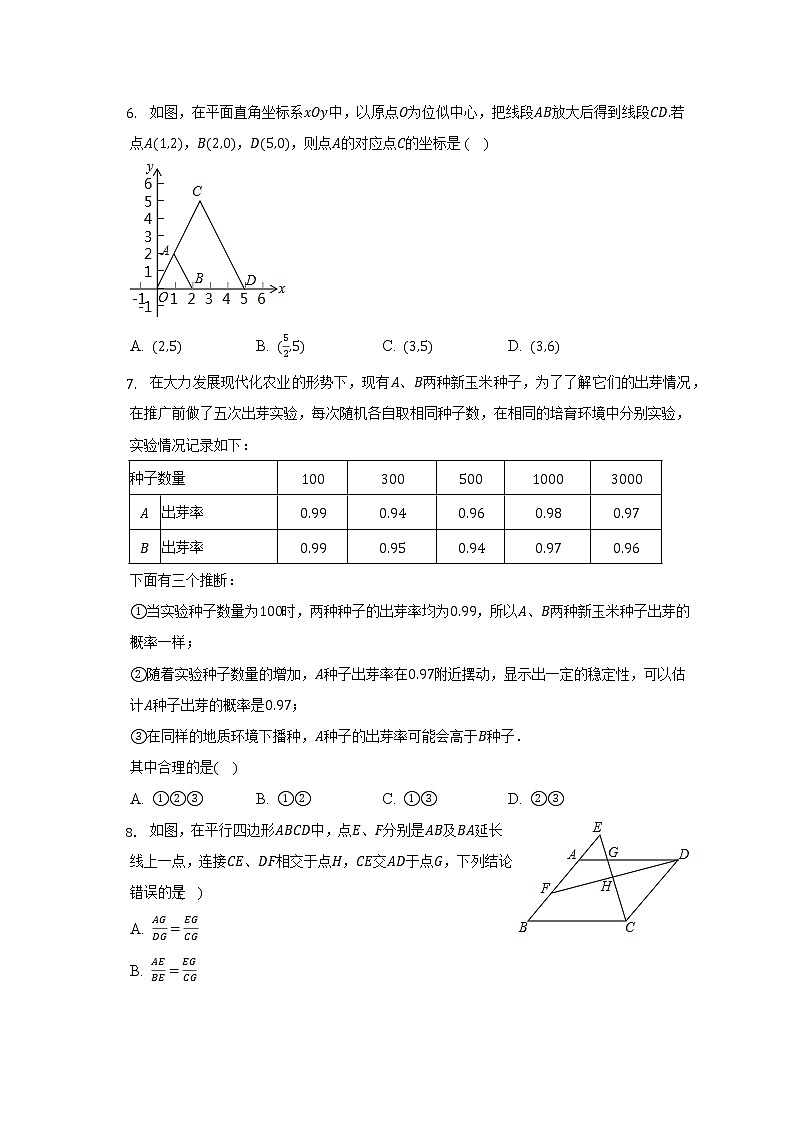
6.    如图，在平面直角坐标系中，以原点为位似中心，把线段放大后得到线段若点，，，则点的对应点的坐标是(    )
    

A.  B.  C.  D.

7.    在大力发展现代化农业的形势下，现有、两种新玉米种子，为了了解它们的出芽情况，在推广前做了五次出芽实验，每次随机各自取相同种子数，在相同的培育环境中分别实验，实验情况记录如下：

下面有三个推断：
当实验种子数量为时，两种种子的出芽率均为，所以、两种新玉米种子出芽的概率一样；
随着实验种子数量的增加，种子出芽率在附近摆动，显示出一定的稳定性，可以估计种子出芽的概率是；
在同样的地质环境下播种，种子的出芽率可能会高于种子．
其中合理的是(    )

A.  B.  C.  D.

8.   如图，在平行四边形中，点、分别是及延长线上一点，连接、相交于点，交于点，下列结论错误的是(    )

A.
B.
C.
D.

9.   如图，在三角形纸片中，，，沿虚线剪下的涂色部分的三角形与相似的是(    )

A.  B.
C.  D.

10. 如图，中，，，点是边的中点，以为底边在其右侧作等腰三角形，使，连结，则的值为(    )

A.  B.  C.  D.

二、填空题（本题共5小题，共15分）

11. 林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组数据：

估计该种幼树在此条件下移植成活的概率为          ．

12. 如图，学校准备在图书馆后面的场地边建一个自行车棚，一边利用图书馆的后墙墙长米，现有总长为米的铁围栏，如果要围成面积为平方米的自行车棚，那么的长为______．
13. 如图给出了一种机器零件的示意图，其中米、米，则的长为______．

14. 如图，在平面直角坐标系中，矩形的顶点在轴的正半轴上，矩形的另一个顶点在轴的正半轴上，矩形的边，，，则点的坐标______．

15. 如图，，，，，在边上取点，使得与相似，则满足条件的长________________．

三、解答题（本题共8小题，共75分）

16. 计算：．
    计算：．
17. 按要求解下列方程：
    因式分解法
    配方法
18. 如图，在正方形中，在边上取中点，连接，过点作交于点、交延长线于点．
    求证：；
    若，求的长．

19. 年国家提出并部署了“新基建”项目，主要包含“特高压，城际高速铁路和城市轨道交通，基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩”等．新基建中高端人才市场就业吸引力报告重点刻画了“新基建”中五大细分领域基站建设，工业互联网，大数据中心，人工智能，新能源汽车充电桩总体的人才与就业机会．如图是其中的一个统计图．
    
    请根据图中信息，解答下列问题：
    填空：图中年“新基建”七大领域预计投资规模的中位数是______亿元；
    甲，乙两位待业人员，仅根据上面统计图中的数据，从五大细分领域中分别选择了“基站建设”和“人工智能”作为自己的就业方向．请简要说明他们选择就业方向的理由各是什么；
    小勇对“新基建”很感兴趣，他收集到了五大细分领域的图标，依次制成编号为，，，，的五张卡片除编号和内容外，其余完全相同，将这五张卡片背面朝上，洗匀放好，从中随机抽取一张不放回，再从中随机抽取一张．请用列表或画状图的方法求抽到的两张卡片恰好是编号为基站建设和人工智能的概率．
20. 如图，九年级数学兴趣小组要测量嵌在某大楼前面的电子屏高度在该大楼正前方的处测得电子屏顶端的仰角为，底端的仰角为从处沿水平地面向正前方走米到达处，测得顶端的仰角为求电子屏的高度结果保留整数
    参考数据：，，，，

21. 某玩具销售商试销某一品种的玩具出厂价为每个元，以每个元销售时，平均每月可销售个，现为了扩大销售，销售商决定降价销售，在原来月份平均销售量的基础上，经月份的试场调查，月份调整价格后，月销售额达到元，已知该玩具价格每个下降元，月销售量将上升个．
    求月份到月份销售额的月平均增长率．
    求三月份时该玩具每个的销售价格．
22. 如图所示，在等腰中，，点由点出发沿方向向点匀速运动，同时点由点出发沿方向向点匀速运动，它们的速度均为连接，设运动时间为，解答下列问题：
    当为何值时，；
    在点，的运动中，是否存在时间，使得与相似？若存在，请求出对应的时间；若不存在，请说明理由．

23. 如图，在中，，，点、分别在边、上，，连接将绕点顺时针方向旋转，记旋转角为．
    问题发现
    当时，______；当时，______；
    拓展研究
    试判断：当时，的大小有无变化？请仅就图的情形给出证明；
    问题解决
    在旋转过程中，的最大值为______．
    
    

答案和解析

1.【答案】 

【解析】解：、等角的余角相等，是必然事件，不符合题意；
B、对顶角相等，是必然事件，不符合题意；
C、垂线段最短，是必然事件，不符合题意；
D、同位角相等，是随机事件，符合题意；
故选：．
根据事件发生的可能性大小判断即可．
本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
 

2.【答案】 

【解析】解：，故与不是同类二次根式，故B错误；
形如的式子是二次根式，故C错误；
若，则，故D错误；
故选：．
根据最简二次根式的定义以及同类二次根式的定义即可求出答案．
本题考查二次根式，解题的关键是正确理解二次根式的相关概念，本题属于基础题型．
 

3.【答案】 

【解析】

【分析】
此题考查了几何概率，计算阴影区域的面积在总面积中占的比例是解题关键．
利用指针落在阴影区域内的概率是：，分别求出概率比较即可．
【解答】
解：、如图所示：指针落在阴影区域内的概率为：；
B、如图所示：指针落在阴影区域内的概率为：；
C、如图所示：指针落在阴影区域内的概率为：；
D、如图所示：指针落在阴影区域内的概率为：，
，
指针落在阴影区域内的概率最大的转盘是：．
故选：．  

4.【答案】 

【解析】解：连接，
，，，
是直角三角形，
；
故选：．
连接，，，，得到是直角三角形，；
本题考查直角三角形，勾股定理；熟练掌握在方格中利用勾股定理求边长，同时判断三角形形状是解题的关键．
 

5.【答案】 

【解析】解：连接，
、分别是、中点，
，
，，
，
，
，
故选：．
连接，根据三角形中位线定理求出，根据勾股定理的逆定理得到，然后求得面积即可．
本题考查的是三角形中位线定理、勾股定理的逆定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．
 

6.【答案】 

【解析】

【分析】
此题主要考查了位似变换，坐标与图形，正确得出对应点的关系是解题关键．在平面直角坐标系中，如果位似变换是以原点为位似中心，位似比为，那么位似图形对应点的坐标的比等于或利用位似图形的性质得出位似比，进而得出对应点坐标的关系．
【解答】
解：以原点为位似中心，把线段放大后得到线段，且，，
，
，
．
故选B．  

7.【答案】 

【解析】解：在大量重复试验时，随着试验次数的增加，可以用一个事件出现的频率估计它的概率，实验种子为，数量太少，出现的频率不能作为、两种新玉米种子出芽的概率，故错误；
随着实验种子数量的增加，种子出芽率在附近摆动，显示出一定的稳定性，可以估计种子出芽的概率是，故正确；
在同样的地质环境下播种，种子的出芽率可能会高于种子，故正确；
故选：．
根据概率的定义和频率的含义，可以判断各个小题中的说法是否正确，本题得以解决．
本题考查利用频率估计概率、概率的意义，解答本题的关键是明确题意，准确判断各个小题中的结论是否成立．
 

8.【答案】 

【解析】解：四边形是平行四边形，
，，，
∽，∽，∽，
，故A正确，不符合题意；
，故B错误，符合题意；
，故C正确，不符合题意；
，
，
，
，
，
，故D正确，不符合题意．
综上，只有符合题意．
故选：．
由平行四边形的性质可得出，，，从而可得∽，∽，∽，进而可得比例式，据此逐个选项判断即可．
本题考查了平行四边形的性质和相似三角形的判定与性质，数形结合并熟练掌握相关性质及定理是解题的关键．
 

9.【答案】 

【解析】

【分析】
此题主要考查了相似三角形的判定，正确利用相似三角形两边比值相等且夹角相等的两三角形相似是解题关键．
根据相似三角形的判定分别进行判断即可得出答案即可．
【解答】
解：在三角形纸片中，，，．
A、，对应边，，
故沿虚线剪下的涂色部分的三角形与不相似，故此选项错误；
B、，对应边，即：，，
故沿虚线剪下的涂色部分的三角形与相似，故此选项正确；
C、，对应边，，
故沿虚线剪下的涂色部分的三角形与不相似，故此选项错误；
D、，
，，
故沿虚线剪下的涂色部分的三角形与不相似，故此选项错误．
故选：．  

10.【答案】 

【解析】解：设与交于点，

，点是边的中点，
，
，
，
，
，
，
，
，
是的垂直平分线，
，
，
，
，
，
，
，
∽，
，
，，
，
，
故选：．
设与交于点，利用直角三角形斜边上的中线等于斜边长的一半，可得，从而证明，得到，，进而得到是的垂直平分线，然后可得，最后证明∽，利用相似三角形的性质即可解答．
本题考查了等腰三角形的性质，相似三角形的判定与性质，直角三角形斜边上的中线，直角三角形斜边上的中线，熟练掌握相似三角形的判定与性质是解题的关键．
 

11.【答案】 

【解析】解：在大量重复实验情况下，频率的稳定值可以作为概率的估计值，即次数越多的频率越接近于概率．
这种幼树移植成活率的概率约为．
故答案为：．
本题主要考查利用频率估计概率．
 

12.【答案】米 

【解析】解：设米，则米，
依题意得：，
整理得：，
解得：，．
又，
应舍去，只取，
即的长为米．
故答案为：米．
设米，则米，根据自行车棚的面积为平方米，即可得出关于的一元二次方程，解之即可得出的值，再结合墙长米，即可得出的长为米．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
 

13.【答案】米 

【解析】解：如图，过点作的垂线，垂足为，则米，
在中，米，，
米，
在中，米，，
米，


米，
故答案为：米．
作垂线，构造直角三角形，在两个特殊锐角的直角三角形中求出、即可．
本题考查解直角三角形的应用，掌握直角三角形的边角关系是正确解答的前提．
 

14.【答案】 

【解析】解：过作轴于，如图所示：
四边形是矩形，
，，，
，
，，
，，
∽，
，即，
，，
，
，
故答案为：
过作轴于，由锐角三角函数定义求出、的长，再证∽，得，求出和即可得出点的坐标．
本题考查了矩形的性质、坐标与图形性质、相似三角形的判定与性质以及锐角三角函数定义等知识；熟练掌握矩形的性质和锐角三角函数定义，证明∽是解题的关键．
 

15.【答案】或或 

【解析】解：分两种情况：
如果∽，
则：：：，
又，
；
如果∽，
则：：，
即，
又，
、是一元二次方程的两根，
解得，，
或．
综上，可知或或．
故答案为或或．
根据相似三角形的性质分情况讨论得出的长．
本题考查相似三角形的判定和性质，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．
 

16.【答案】解：




；






． 

【解析】利用特殊角的三角函数值和二次根式的化简求值即可；
利用数的乘方，二次根式的化简求值即可．
本题考查了二次根式的混合运算，特殊角的三角函数值，解题的关键是掌握二次根式的混合运算，特殊角的三角函数值．
 

17.【答案】解：
分解因式得：，
，，
解方程得：，．
，
变形得：，
配方得：，
即，
开方得：，
解得：，． 

【解析】分解因式得到，推出方程，，求出方程的解即可．
变形后得到，配方推出，开方得到方程，求出方程的解即可．
本题主要考查对解一元二次方程，解一元一次方程等知识点的理解和掌握，能选择适当的方法解一元二次方程是解此题的关键．
 

18.【答案】证明：四边形是正方形，，
，，，
，，
；

解：四边形是正方形，
，，
为的中点，
，
在中，由勾股定理得：，
，
，
，
解得：，
，
． 

【解析】根据正方形的性质和得出，，根据平行线的性质得出，再根据相似三角形的判定即可得证；
根据正方形的性质得出，，求出，根据勾股定理求出，根据相似得出比例式，代入求出即可求得的长．
本题考查了平行线的性质，勾股定理，正方形的性质，相似三角形的性质和判定等知识点，能综合运用知识点进行推理和计算是解此题的关键．
 

19.【答案】解：年“新基建”七大领域预计投资规模按照从小到大排列为、、、、、、，
图中年“新基建”七大领域预计投资规模的中位数是亿元，
故答案为：；
甲更关注在线职位的增长率，在“新基建”五大细分领域中，年一季度“基站建设”在线职位与年同期相比增长率最高；
乙更关注预计投资规模，在“新基建”五大细分领域中，“人工智能”在年预计投资规模最大；
列表如下：

由表可知，共有种等可能结果，其中抽到“”和“”的结果有种，
抽到的两张卡片恰好是编号为基站建设和人工智能的概率． 

【解析】根据统计图，将年“新基建”七大领域预计投资规模按照从小到大排列，再利用中位数定义求解可得；
分别从年一季度“基站建设”在线职位与年同期相比增长率和年预计投资规模角度分析求解可得；
列表得出所有等可能结果，从中找到符合条件的结果数，根据概率公式求解可得．
本题主要考查条形统计图、折线统计图和列表法与树状图法求概率，根据条形图得出解题所需数据及画树状图列出所有等可能结果是解题的关键．
 

20.【答案】解：设楼高为米，
在中，，
是等腰直角三角形，
米，
米，
在中，米，
，
解得：，
米，
在中，米，
米，
答：电子屏的高度约为米． 

【解析】设楼高为米，得到米，然后解直角三角形求出，即可解决问题．
此题是解直角三角形的应用仰角俯角问题，熟练掌握仰角俯角的定义和锐角三角函数定义是解题的关键．
 

21.【答案】解：设月份到月份销售额的月平均增长率为，由题意得：



，舍去
月份到月份销售额的月平均增长率为．
设三月份时该玩具的销售价格在每个元销售的基础上下降元，由题意得：



，
当时，月份该玩具的销售价格为：，不合题意，舍去
，月份该玩具的销售价格为：元
月份该玩具的销售价格为元． 

【解析】设月份到月份销售额的月平均增长率为，由题意得关于的一元二次方程，求解，并保留符合题意的答案即可；
设三月份时该玩具的销售价格在每个元销售的基础上下降元，根据实际售价乘以降价后的销量等于月份的销售额，列方程求解，并验证是否符合题意，从而问题可解．
本题考查了一元二次方程在实际问题中的应用，明确单价乘以销量等于销售额及平均增长率类型习题的计算方法，是解题的关键．
 

22.【答案】解：如图，过点作于点，
在等腰中，，，则．
在直角中，由勾股定理得到：．
，，
．
∽．
，即．
解得；

存在．理由如下：
当时，∽，
，即，
解得，
当时，∽，
，即，
解得．
答：存在时间为或时，使得与相似． 

【解析】如图，当时，过点作于点，构造直角三角形和相似三角形，利用勾股定理和相似三角形的对应边成比例列出关于的方程并解答；
根据等腰三角形和相似三角形的判定和性质分两种情况说明即可．
本题考查了相似三角形的判定和性质、等腰三角形的性质，解决本题的关键是动点变化过程中形成不同的等腰三角形．
 

23.【答案】解：在中，，
，
，
，
，
，
，
，
，
，
故答案为；
如图，
，
，
，
，
，
，
，
，
，
，
，
故答案为；
当时，的大小没有变化，
证明：在中，
，，
，，
，
，
，，
，
，
，
，
在和中，
∽，
；
如题中的图，当点在的延长线上时，最大，其最大值为，
在中，，
，
，
由知，，
，
，
，
故答案为． 

【解析】本题是几何变换综合题，主要考查了等腰三角形的性质，平行线的性质，以及相似三角形的判定和性质．
利用等腰三角形的性质判断出，，进而得出，得出，即可得出结论；
同的方法，即可得出结论；
利用两边成比例，夹角相等，判断出∽，即可得出结论；
判断出点在的延长线上时，最大，再求出，即可得出结论．