第10讲 勾股定理与勾股定理逆定理-【专题突破】2022-2023学年八年级数学上学期重难点及章节分类精品讲义(浙教版) （原卷版+解析）

这是一份第10讲 勾股定理与勾股定理逆定理-【专题突破】2022-2023学年八年级数学上学期重难点及章节分类精品讲义(浙教版) （原卷版+解析），文件包含第10讲勾股定理与勾股定理逆定理-专题突破2022-2023学年八年级数学上学期重难点及章节分类精品讲义浙教版解析版docx、第10讲勾股定理与勾股定理逆定理-专题突破2022-2023学年八年级数学上学期重难点及章节分类精品讲义浙教版原卷版docx等2份试卷配套教学资源，其中试卷共40页， 欢迎下载使用。

直角三角形勾股定理
在Rt△ABC中，两直角边的平方和=斜边的平方，即
常见变形：；；
注意事项：当直角三角形的给出的两边没有说明是什么边长时，利用勾股定理求长度时通常需要分类讨论
直角三角形求长度其他常用相关性质有：
直角三角形斜边上的中线=½斜边长
等腰三角形的两腰长相等；
等腰三角形的“三线合一”
中垂线的性质定理；
勾股定理常见面积模型
【类题训练】
1．直角三角形的两条边长a，b满足，则其斜边长为（ ）
A．5B．C．4或5D．或5
2．如图，在Rt△ABC中，∠C＝90，AC＝3，BC＝4，CD是△ABC的中线，则AD的长为（ ）
A．2B．2.5C．4D．5
3．如图，在3×3的正方形网格中，若小正方形的边长是1，则任意两个格点间的距离不可能是（ ）
A．2B．2C．D．
4．我国是最早了解勾股定理的国家之一．据《周髀算经》记载，勾股定理的证明是在商代由商高发现的，故又称之为“商高定理”；三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释，又给出了另外一个证明．古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用．下面四幅图中，不能证明勾股定理的是（ ）
A． B． C． D．
5．如图，有一个水池，水面是一边长为8尺的正方形，在水池中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池的一边的中点，它的顶端恰好到达池边的水面，这根芦苇的长度是（ ）尺．
A．7.5B．8C．D．9
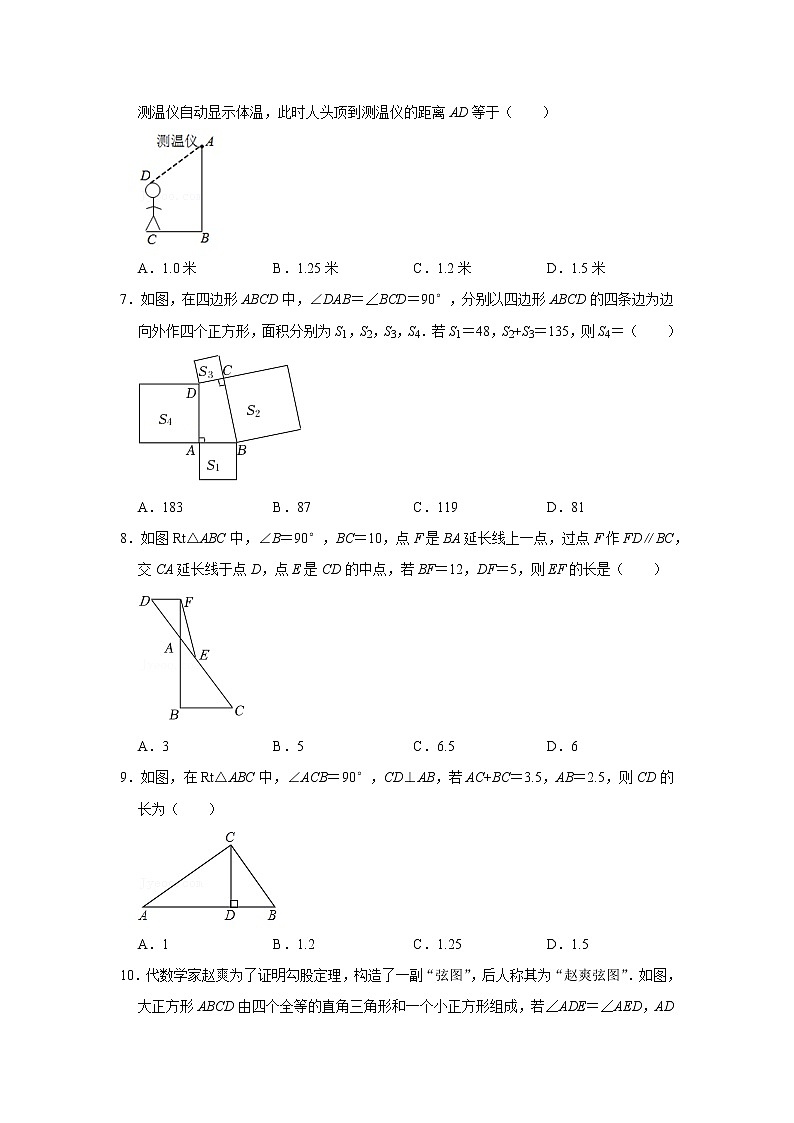
6．为预防新冠疫情，学校大门入口的正上方A处装有红外线激光测温仪（如图所示），测温仪离地面的距离AB＝2.3米，当人体进入感应范围内时，测温仪就会自动测温并报告人体体温．当身高为1.7米的学生CD正对门缓慢走到离门0.8米处时（即BC＝0.8米），测温仪自动显示体温，此时人头顶到测温仪的距离AD等于（ ）
A．1.0米B．1.25米C．1.2米D．1.5米
7．如图，在四边形ABCD中，∠DAB＝∠BCD＝90°，分别以四边形ABCD的四条边为边向外作四个正方形，面积分别为S1，S2，S3，S4．若S1＝48，S2+S3＝135，则S4＝（ ）
A．183B．87C．119D．81
8．如图Rt△ABC中，∠B＝90°，BC＝10，点F是BA延长线上一点，过点F作FD∥BC，交CA延长线于点D，点E是CD的中点，若BF＝12，DF＝5，则EF的长是（ ）
A．3B．5C．6.5D．6
9．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，若AC+BC＝3.5，AB＝2.5，则CD的长为（ ）
A．1B．1.2C．1.25D．1.5
10．代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”．如图，大正方形ABCD由四个全等的直角三角形和一个小正方形组成，若∠ADE＝∠AED，AD＝4，则△ADE的面积为（ ）
A．24B．6C．2D．2
11．勾股定理在平面几何中有着不可替代的重要地位，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载，如图1是由边长均为1的小正方形和Rt△ABC构成，可以用其面积关系验证勾股定理，将图1按图2所示“嵌入”长方形LMJK，则该长方形的面积为（ ）
A．60B．100C．110D．121
12．如图，将一副三角尺叠放在一起，若AB＝2cm，则AF的长为 cm．
13．对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，若AD＝3，BC＝5，则AB2+CD2＝ ．
14．如图，一架梯子AB斜靠在某个胡同竖直的左墙上，顶端在点A处，底端在水平地面的点B处，保持梯子底端B的位置不变，将梯子斜靠在竖直的右墙上，此时梯子的顶端在点E处．已知顶端A距离地面的高度AC为2米，BC为1.5米．
（1）梯子的长为 米；
（2）若顶端E距离地面的高度EF比AC多0.4米，则胡同的宽CF为 米．
15．如图，已知，∠MON＝∠BAC＝90°，且点A在OM上运动，点B在ON上运动，若AB＝8，AC＝6，则OC的最大值为 ．
16．如图，在Rt△ABC中，∠ABC＝90°，，，分别以Rt△ABC的三条边AC、AB、BC为直径画半圆，则两个月牙形图案的面积之和（阴影部分）为 ．
17．在一条东西走向的河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原由，C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A，H，B在一条直线上），并新修一条路CH，测得CB＝3km，CH＝2.4km，BH＝1.8km．求原来的路线AC的长．
18．如图，在△ABC中，AC＝BC＝6，E为BC边上一点，且CE＝2，AE＝2．
（1）求AB的长；
（2）点F为AB边上的动点，当△BEF为等腰三角形时，求AF的长．
19．如图，在△DEF中，∠D＝90°，DE＝16cm，EF＝20cm，P，Q是△DEF的边上的两个动点，其中点P从点E开始沿E→D方向运动，且速度为每秒1cm，点Q从点D开始沿D→F→E方向运动，且速度为每秒2m，它们同时出发，设出发的时间为ts．
（1）DF＝ cm．
（2）当点P在边EF的垂直平分线上时，t＝ s．
（3）当点Q在边EF上时，求使△DFQ成为等腰三角形的运动时间．
考点二 勾股定理的逆定理
【知识点睛】
勾股定理的逆定理
在△ABC中，若两边的平方和=第三边的平方，则该△为直角三角形
即在△ABC中，若，则△ABC为直角三角形，且∠C为直角
【类题训练】
1．以下列各组线段为边作三角形，不能作出直角三角形的是（ ）
A．3，7，8B．6，8，10
C．1，2，D．0.3，0.4，0.5
2．如图，小正方形的边长均为1，A、B、C是小正方形的顶点，则∠ACB的度数是（ ）
A．30°B．45°C．60°D．90°
3．如图，某海域有相距10海里的两个小岛A和C，甲船先由A岛沿北偏东70°方向走了8海里到达B岛，然后再从B岛走了6海里到达C岛，此时甲船位于B岛的（ ）
A．北偏东20°方向上B．北偏西20°方向上
C．北偏西30°方向上D．北偏西40°方向上
4．如图，正方形网格中每一个小正方形的边长为1，小正方形的顶点为格点，点A，B，C为格点，点D为AC与网格线的交点，则∠ADB﹣∠ABD＝ ．
5．如图，四边形ABCD中，AB⊥BC，AB＝4，BC＝3，AD＝12，CD＝13，则四边形ABCD的面积是 ．
6．如图，点A、B、C在正方形网格点上，则∠ABC+∠ACB＝ ．
7．如图，方格中的点A、B、C、D、E称为“格点”（格线的交点），以这5个格点中的3点为顶点画三角形，共可以画 个直角三角形．
8．如图，点B为x轴上的一个动点，点A的坐标为（0，4），点C的坐标为（4，1），CE⊥x轴于E点，当点B的坐标为 时，△ABC为直角三角形．
9．如图，在4×4的正方形网格中有两个格点A、B，连接AB，在网格中再找一个格点C，使得△ABC是等腰直角三角形，满足条件的格点C有 个．
10．如图所示，四边形ABCD，∠A＝90°，AB＝3m，BC＝12m，CD＝13m，DA＝4m．
（1）求四边形ABCD的面积；
（2）如图2，以A为坐标原点，以AB、AD所在直线为x轴、y轴建立直角坐标系，点P在y轴上，若S△PBD＝S四边形ABCD，求P的坐标．
11．在一次“探究性学习”中，老师设计了如下数表：
（1）观察上表，用含n（n＞1，且n为整数）的代数式表示a，b，c，则a＝ ，b＝ ，c＝ ．
（2）在（1）的条件下判断：以a，b，c为边的三角形是否为直角三角形？证明你的结论．
12．如图，在△ABC中，AB＝AC，AD⊥BC于点D，∠CBE＝45°，BE分别交AC，AD于点E、F．
（1）如图1，若AB＝13，BC＝10，求AF的长度；
（2）如图2，若AF＝BC，求证：BF2+EF2＝AE2．
图形
结论
总结
当分别以直角三角形的三边为边（或底边、半径）做规则的正方形、等边三角形、等腰直角三角形、半圆时，均满足两直角边所做图形的面积和等于斜边所做图形的面积
n
2
3
4
5
6
…
a
22﹣1
32﹣1
42﹣1
52﹣1
62﹣1
…
b
4
6
8
10
12
…
C
22+1
32+1
42+1
52+1
62+1
…