北师大版数学九上 期末数学试卷（含答案）

九年级（上）期末数学试卷

（总分：120分   时间：90分钟）

一、选择题（本题包括10小题，每小题3分，共30分。每小题只有1个选项符合题意）

1．9的平方根是（　　）

A．±3 B．3 C．﹣3 D．±

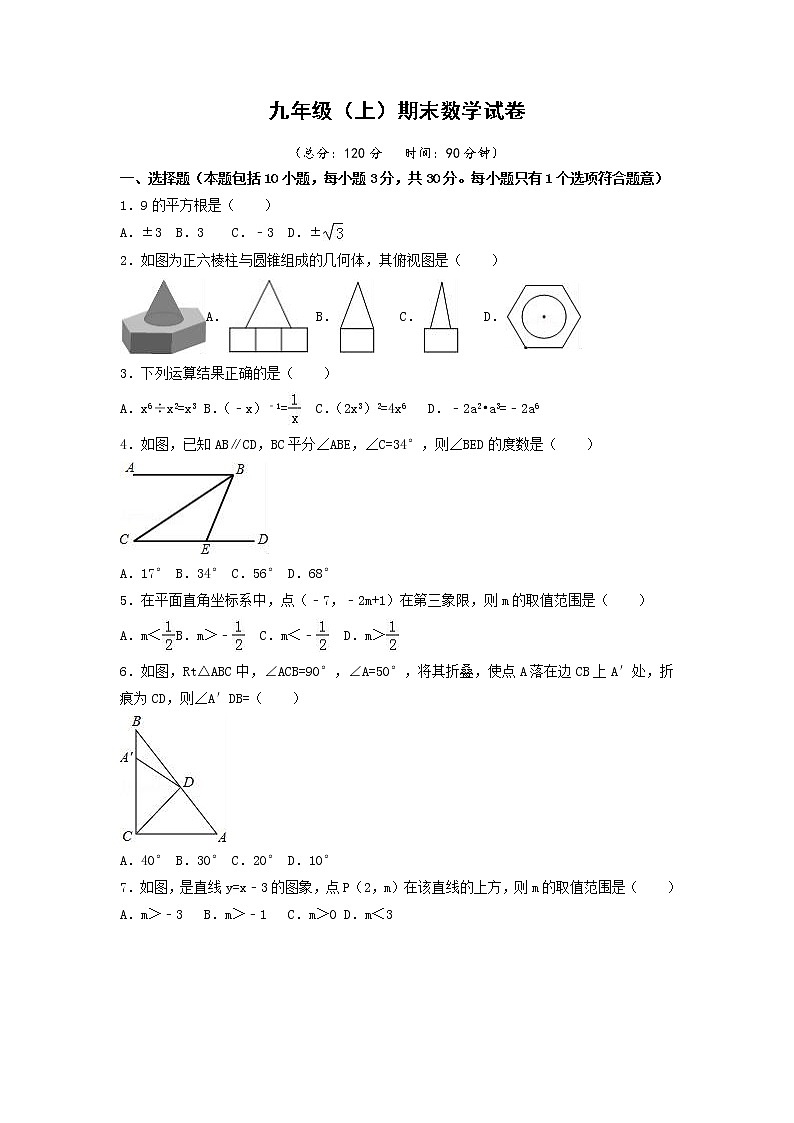
2．如图为正六棱柱与圆锥组成的几何体，其俯视图是（　　）

A． B． C． D．

3．下列运算结果正确的是（　　）

A．x6÷x2=x3 B．（﹣x）﹣1= C．（2x3）2=4x6 D．﹣2a2•a3=﹣2a6

4．如图，已知AB∥CD，BC平分∠ABE，∠C=34°，则∠BED的度数是（　　）

A．17° B．34° C．56° D．68°

5．在平面直角坐标系中，点（﹣7，﹣2m+1）在第三象限，则m的取值范围是（　　）

A．m＜ B．m＞﹣ C．m＜﹣ D．m＞

6．如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=（　　）

A．40° B．30° C．20° D．10°

7．如图，是直线y=x﹣3的图象，点P（2，m）在该直线的上方，则m的取值范围是（　　）

A．m＞﹣3 B．m＞﹣1 C．m＞0 D．m＜3

8．如图，在矩形ABCD中，边AB的长为3，点E，F分别在AD，BC上，连接BE，DF，EF，BD．若四边形BFDE是菱形，且OE=AE，则边BC的长为（　　）

A．2 B．3 C．  D．6

9．如图，半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD，已知DE=6，∠BAC+∠EAD=180°，则弦BC的长等于（　　）

A． B． C．8 D．6

10．若二次函数y=ax2+bx+c（a＜0）的图象经过点（2，0），且其对称轴为x=﹣1，则使函数值y＞0成立的x的取值范围是（　　）

A．x＜﹣4或x＞2 B．﹣4≤x≤2 C．x≤﹣4或x≥2 D．﹣4＜x＜2

二、填空题（本题包括7小题，每空3分，共21分）

11．计算|﹣2|+2cos45°=　 　．

12．一元二次方程x2+9x=0的解是　 　．

13．如图，正六边形ABCDEF的边长为2，则对角线AF=         ．

14．比较大小：sin57°　 　tan57°．

15．如图，在河两岸分别有A、B两村，现测得三点A、B、D在一条直线上，A、C、E在一条直线上，若BC∥DE，DE=90米，BC=70米，BD=20米，那么A、B两村间的距离为　 　米．

16．如图，在平面直角坐标系中，函数y=（x＞0常数k＞0）的图象经过点A（1，2），B（m，n）（m＞1），过点B作y轴的垂线，垂足为C，若△ABC面积为2，求点B的坐标　  　．

17．如图，O为矩形ABCD对角线的交点，M为AB边上任一点，射线ON⊥OM于点O，且与BC边交于点N，若AB=4，AD=6，则四边形OMBN面积的最大值为　  　．

三、解答题（共9小题，满分69分）

18．解方程： =+1．

19．如图，Rt△ABC中，∠C=90°，用直尺和圆规在边BC上找一点D，使D到AB的距离等于CD．（保留作图痕迹，不写作法）

20．已知，如图，在△ABC中，点D为线段BC上一点，BD=AC，过点D作DE∥AC且DE=BC，求证：∠E=∠CBA．

21．如图为一种平板电脑保护套的支架侧视图，AM固定于平板电脑背面，与可活动的MB、CB部分组成支架，为了观看舒适，可以调整倾斜角∠ANB的大小，但平板的下端点N只能在底座边CB上．不考虑拐角处的弧度及平板电脑和保护套的厚度，绘制成图（见答题纸），其中AN表示平板电脑，M为AN上的定点，AN=CB=20 cm，AM=8 cm，MB=MN，根据以上数据，判断倾斜角∠ANB能小于30°吗？请说明理由．

22．为庆祝商都正式营业，商都推出了两种购物方案．方案一：非会员购物所有商品价格可获九五折优惠，方案二：如交纳300元会费成为该商都会员，则所有商品价格可获九折优惠．

（1）以x（元）表示商品价格，y（元）表示支出金额，分别写出两种购物方案中y关于x的函数解析式；

（2）若某人计划在商都购买价格为5880元的电视机一台，请分析选择哪种方案更省钱？

23．小励同学有面额10元.20元.50元和100元的纸币各一张，分别装入大小外观完全样的四个红包中，每个红包里只装入一张纸币，若小励从中随机抽取两个红包．

（1）请用树状图或者列表的方法，求小励取出纸币的总额为70元的概率；

（2）求小励取出纸币的总额能购买一件价格为120元文具的概率．

24．如图，BC是圆O的弦，CF是圆O切线，切点为C，经过点B作MN⊥CF于E，且∠CBM=135°，过G的直线分别与圆O，MN交于A，D两点．

（1）求证：MN是圆O的切线；

（2）当∠D=30°，BD=时，求圆O的半径r．

25．已知二次函数y═ax2+bx+c（a＞0）的图象与x轴交于A（﹣5，0）、B（1，0）两点，与y轴交于点C，抛物线的顶点为D．

（1）直接写出顶点D、点C的坐标（用含a的代数式表示）；

（2）若∠ADC=90°，试确定二次函数的表达式．

26．如图，三角形有一边上的中线长恰好等于这边的长，那么这个三角形可称为“等中三角形”，

探索体验

（1）如图①，点D是线段AB的中点，请画一个△ABC，使其为“等中三角形”．

（2）如图②，在 Rt△ABC中，∠C=90°，AC=2，BC=，判断△ABC是否为“等中三角形”，并说明理由．

拓展应用

（3）如图③，正方形ABCD木板的边长AB=6，请探索在正方形木板上是否存在点P，使△ABP为面积最大的“等中三角形”？若存在，求出CP的长；若不存在，请说明理由．

九年级（上）期末数学试卷

参考答案

一、选择题

1．【考点】平方根．

【分析】根据平方与开平方互为逆运算，可得一个正数的平方根．

【解答】±，故选：A．

2．【考点】简单组合体的三视图．

【分析】从几何体上方观察，得到俯视图即可．

【解答】如图为正六棱柱与圆锥组成的几何体，其俯视图是．故选D

3．【考点】同底数幂的除法；幂的乘方与积的乘方；单项式乘单项式；负整数指数幂．

【分析】根据同底数幂的除法、幂的乘方、单项式的乘法计算即可．

【解答】A、x6÷x2=x4，错误；B、（﹣x）﹣1=﹣，错误；C、（2x3）2=4x6，正确；D、﹣2a2•a3=﹣2a5，错误；故选C

4．【考点】平行线的性质．

【分析】首先由AB∥CD，求得∠ABC的度数，又由BC平分∠ABE，求得∠CBE的度数，然后根据三角形外角的性质求得∠BED的度数．

【解答】∵AB∥CD，∴∠ABC=∠C=34°.∵BC平分∠ABE，∴∠CBE=∠ABC=34°，∴∠BED=∠C+∠CBE=68°．故选D．

5．【考点】点的坐标．

【分析】点在第三象限的条件是：横坐标是负数，纵坐标是负数，可得﹣2m+1＜0，求不等式的解即可．

【解答】∵点在第三象限，∴点的横坐标是负数，纵坐标也是负数，即﹣2m+1＜0，解得m＞．故选D．

6．【考点】三角形内角和定理；三角形的外角性质；翻折变换（折叠问题）．

【分析】由三角形的一个外角等于与它不相邻的两个内角的和，得∠A′DB=∠CA'D﹣∠B，又折叠前后图形的形状和大小不变，∠CA'D=∠A=50°，易求∠B=90°﹣∠A=40°，从而求出∠A′DB的度数．

【解答】∵Rt△ABC中，∠ACB=90°，∠A=50°，∴∠B=90°﹣50°=40°.∵将其折叠，使点A落在边CB上A′处，折痕为CD，则∠CA'D=∠A.∵∠CA'D是△A'BD的外角，∴∠A′DB=∠CA'D﹣∠B=50°﹣40°=10°．故选：D．

7．【考点】一次函数图象上点的坐标特征．

【分析】把x=2代入直线的解析式求出y的值，再根据点P（2，m）在该直线的上方即可得出m的取值范围．

【解答】当x=2时，y=2﹣3=﹣1，∵点P（2，m）在该直线的上方，∴m＞﹣1．故选B．

8．【考点】矩形的性质；菱形的性质．

【分析】根据矩形的性质和菱形的性质得∠ABE=∠EBD=∠DBC=30°，解直角三角形BDC，即可求出BC的长．

【解答】∵四边形ABCD是矩形，∴∠A=90°，∠ABC=90°，AB=CD，即EA⊥AB.∵四边形BFDE是菱形，∴BD⊥EF.∵OE=AE，∴点E在∠ABD的角平分线上，∴∠ABE=∠EBD.∵四边形BFDE是菱形，∴∠EBD=∠DBC，∴∠ABE=∠EBD=∠DBC=30°.∵AB的长为3，∴BC=3，故选B．

9．【考点】圆周角定理；勾股定理．

【分析】首先延长CA，交⊙A于点F，易得∠BAF=∠DAE，由圆心角与弦的关系，可得BF=DE，由圆周角定理可得：∠CBF=90°，然后由勾股定理求得弦BC的长．

【解答】延长CA，交⊙A于点F.∵∠BAC+∠BAF=180°，∠BAC+∠EAD=180°，∴∠BAF=∠DAE，∴BF=DE=6.∵CF是直径，∴∠ABF=90°，CF=2×5=10，∴BC==8．故选C．

10．【考点】二次函数与不等式（组）．

【分析】由抛物线与x轴的交点及对称轴求出另一个交点坐标，根据抛物线开口向下，根据图象求出使函数值y＞0成立的x的取值范围即可．

【解答】∵二次函数y=ax2+bx+c（a＜0）的图象经过点（2，0），且其对称轴为x=﹣1，∴二次函数的图象与x轴另一个交点为（﹣4，0），∵a＜0，∴抛物线开口向下，则使函数值y＞0成立的x的取值范围是﹣4＜x＜2．故选D．

二、填空题

11．【考点】实数的运算；特殊角的三角函数值．

【分析】直接利用绝对值的性质结合特殊角的三角函数值代入化简即可．

【解答】原式=2﹣+2×=2﹣+=2．

12．【考点】解一元二次方程﹣因式分解法．

【分析】因式分解法求解可得．

【解答】∵x（x+9）=0，∴x=0或x+9=0，解得：x=0或x=﹣9，　

13．【考点】正多边形和圆．

【分析】作BG⊥AF，垂足为G．构造等腰三角形ABF，在直角三角形ABG中，求出AG的长，即可得出AF．

【解答】作BG⊥AF，垂足为G．如图所示.∵AB=BF=2，∴AG=FG，∵∠ABF=120°，∴∠BAF=30°，∴AG=AB•cos30°=2×=，∴AC=2AG=2；故答案为2．

14．【考点】锐角三角函数的增减性．

【分析】根据正弦函数的增减性，正切函数的增减性，可得答案．

【解答】∵sin57＜sin90°=1，tan57°＞tan45°=1，∴tan57°＞sin57°，故答案为：＜．

15．【考点】相似三角形的应用．

【分析】由BC∥DE，可得，△ABC∽△ADE，进而利用对应边成比例求解线段的长度．

【解答】由题意可得，△ABC∽△ADE，∴，即，解得AB=70米．

16．【考点】反比例函数综合题．

【分析】由于函数y=（x＞0常数k＞0）的图象经过点A（1，2），把（1，2）代入解析式即可确定k=2，依题意BC=m，BC边上的高是2﹣n=2﹣，根据三角形的面积公式得到关于m的方程，解方程即可求出m，然后把m的值代入y=，即可求得B的纵坐标，最后就求出点B的坐标．

【解答】∵函数y=（x＞0常数k＞0）的图象经过点A（1，2），∴把（1，2）代入解析式得2=，∴k=2.∵B（m，n）（m＞1），∴BC=m，当x=m时，n=，∴BC边上的高是2﹣n=2﹣，而S△ABC=m（2﹣）=2，∴m=3，∴把m=3代入y=，∴n=，∴点B的坐标是（3，）．故答案为：（3，）．

17．【考点】相似三角形的判定与性质；一次函数的性质；矩形的性质．

【分析】（方法一）过点O作OE⊥AB于点E，作OF⊥BC于点F，易证得△FOM∽△EON，然后由相似三角形的对应边成比例结合分割图形求面积法即可得出S四边形OMBN=﹣x+6，根据一次函数的性质即可解决最值问题；（方法二）过点O作OE⊥AB于点E，作OF⊥BC于点F，当点M和点E重合、点N和点F重合时，四边形OMBN面积取最大值，根据矩形的面积即可得出结论．

【解答】（方法一）过点O作OE⊥AB于点E，作OF⊥BC于点F，如图所示．∵四边形ABCD为矩形，AB=4，AD=6，∴OE=3，OF=2，OE⊥OF，∴∠EOM+∠FOM=90°，∵∠FON+∠FOM=90°，∴∠EOM=∠FON．∵∠OEM=∠OFN=90°，∴△FON∽△EOM，∴OM：ON=OE：OF=3：2，∴=．设ME=x（0≤x≤2），则FN=x，∴S四边形OMBN=S矩形EBFO﹣S△EOM+S△FON=2×3﹣×3x+×2×x=﹣x+6，∴当x=0时，S四边形OMBN取最大值，最大值为6．故答案为：6．（方法二）过点O作OE⊥AB于点E，作OF⊥BC于点F，当点M和点E重合、点N和点F重合时，四边形OMBN面积取最大值，如图所示．∵S矩形EBFO=2×3=6，∴四边形OMBN面积的最大值为6．故答案为：6

三、解答题（共9小题，满分72分）

18．【考点】解分式方程．

【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

【解答】去分母得：﹣x+3=1+x﹣4，

移项合并得：﹣2x=﹣6，

解得：x=3，

经检验x=3是分式方程的解．

19．【考点】作图—基本作图；角平分线的性质．

【分析】作∠BAC的平分线交BC边于点D，则点D即为所求．

【解答】如图，点D即为所求．

20．【考点】全等三角形的判定与性质；平行线的性质．

【分析】根据平行线的性质可得∠C=∠EDB，再证明△EBD≌△BAC，根据全等三角形的性质可得∠E=∠CBA．

【解答】∵DE∥AC，∴∠C=∠EDB，

在△EBD和△BAC中，

∴△EBD≌△BAC（SAS），

∴∠E=∠CBA．

21．【考点】解直角三角形的应用﹣坡度坡角问题．

【分析】根据∠ANB=30°时，作ME⊥CB，垂足为E，根据锐角三角函数的定义求出EB及BN的长，进而可得出结论．

【解答】当∠ANB=30°时，作ME⊥CB，垂足为E，

∵MB=MN，∴∠B=∠ANB=30°．

在Rt△BEM中，∵cosB=，

∴EB=MB•cosB=（AN﹣AM）•cosB=6cm．

∵MB=MN，ME⊥BC，

∴BN=2BE=12cm．

∵CB=AN=20cm，且12＞20，

∴此时N不在CB边上，与题目条件不符，随着∠ANB度数的减小，BN的长度增加，

∴倾斜角不可以小于30°．

22．【考点】一次函数的应用．

【分析】（1）根据两种购物方案让利方式分别列式整理即可；

（2）分别把x=5880，代入（1）中的函数求得数值，比较得出答案即可．

【解答】（1）方案一：y=0.95x；

方案二：y=0.9x+300；

（2）当x=5880时，

方案一：y=0.95x=5586（元），

方案二：y=0.9x+300=5592（元），

5586＜5592

所以选择方案一更省钱．

23．【考点】列表法与树状图法．

【分析】（1）先利用树状图展示所有12种等可能的结果数，再找出取出纸币的总额为70元的结果数，然后根据概率公式计算；（2）根据（1）中树状图找到取出纸币的总额大于或等于120元的结果数，根据概率公式计算可得．

【解答】（1）画树状图为：

共有12种等可能的结果数，其中取出纸币的总额为70元的结果数为2，

所以取出纸币的总额为70元的概率==；

（2）小励取出纸币的总额能购买一件价格为120元文具的概率为=．

24．【考点】切线的判定与性质．

【分析】（1）连接OB、OC，证明OC⊥CE即可．因为MN是⊙O的切线，所以OB⊥MN．因∠CBN=45°可得∠OBC=∠OCB=∠BCE=45°，所以∠OCE=90°，得证；（2）可证四边形BOCE为正方形，所以半径等于CE，可设半径为r，在△BCE中表示BE；在△CDE中表示DE，根据BD的长得方程求解．

【解答】（1）证明：连接OB、OC．

∵MN是⊙O的切线，∴OB⊥MN，

∵∠CBM=135°，∴∠CBN=45°，

∴∠OBC=45°，∠BCE=45°．

∵OB=OC，∴∠OBC=∠OCB=45°．

∴∠OCE=90°，∴CE是⊙O的切线；

（2）解：∵OB⊥BE，CE⊥BE，OC⊥CE，

∴四边形BOCE是矩形，

又OB=OC，∴四边形BOCE是正方形，

∴BE=CE=OB=OC=r．

在Rt△CDE中，∵∠D=30°，CE=r，

∴DE=r．

∵BD=2，∴r+r=2，

∴r=﹣，即⊙O的半径为﹣．

25．【考点】抛物线与x轴的交点；待定系数法求二次函数解析式．

【分析】（1）根据抛物线y═ax2+bx+c（a＞0）与x轴的交点可得解析式为y=a（x+5）（x﹣1）=ax2+4ax﹣5a=a（x+2）2﹣9a，从而得出答案；（2）由A、D、C的坐标得出AD2、CD2、AC2，根据∠ADC=90°知AD2+CD2=AC2，据此列出关于a的方程，解之可得a的值，从而得出答案．

【解答】（1）∵二次函数y═ax2+bx+c（a＞0）的图象与x轴交于A（﹣5，0）、B（1，0）两点，

∴抛物线的解析式为y=a（x+5）（x﹣1）=ax2+4ax﹣5a=a（x+2）2﹣9a，

则点D的坐标为（﹣2，﹣9a），点C的坐标为（0，﹣5a）；

（2）∵A（﹣5，0）、D（﹣2，﹣9a）、C（0，﹣5a），

∴AD2=（﹣2+5）2+（﹣9a﹣0）2=81a2+9，CD2=（﹣2﹣0）2+（﹣9a+5a）2=16a2+4，

AC2=（0+5）2+（﹣5a﹣0）2=25a2+25，

∵∠ADC=90°，∴AD2+CD2=AC2，即81a2+9+16a2+4=25a2+25，

解得：a=±，

∵a＞0，∴a=﹣，

则该二次函数的解析式为y=﹣（x+2）2﹣．

26．【考点】四边形综合题．

【分析】（1）通过同圆的半径相等，取DC=AB，则△ABC就是所求作的等中三角形；（2）作中线BD，根据勾股定理求中线BD=AC，则△ABC是“等中三角形”；（3）分别以△ABP三边画等中三角形，对比后得图5中的等中三角形的面积最大，求出此时的CP的长即可．

【解答】解：（1）如图1，

作法：①以D为圆心，以AB为半径画圆，在圆上任意取一点C，

②连接AC、BC，

则△ABC就是所求作的“等中三角形”；

（2）△ABC是“等中三角形”，理由是：

如图2，取AC的中点D，连接BD，

∵AC=2，∴CD=AC=1，

∵∠ACB=90°，

由勾股定理得：BD==2，

∴BD=AC，∴△ABC是“等中三角形”，

（3）分三种情况：

①当中线长BE=AP时，如图3，

②当中线长AE=PB时，如图4，

③当中线长PE=AB时，如图5，

由三个图形可得：图5中的等中三角形的面积最大，

此时，P是DC的中点，

∴PC=CD==3．