
2022年广州中考数学终极押题密卷2
展开
这是一份2022年广州中考数学终极押题密卷2,共31页。
2022年广州中考数学终极押题密卷2
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列各组数中,互为相反数的是( )
A.6和﹣6 B.﹣6和 C.﹣6和 D.和6
2.(3分)(2021秋•八公山区期末)下列图案是几种名车的标志,请你指出,在这几个图案中是轴对称图形的共有( )
A.1个 B.2个 C.3个 D.4个
3.(3分)(2022春•宁海县期中)一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示.若每双鞋的销售利润相同,则该店主最应关注的销售数据是下列统计量中的( )
鞋的尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量双
1
2
5
11
7
3
1
A.平均数 B.方差 C.众数 D.中位数
4.(3分)(2022•滨海新区一模)如图是由几个相同的正方体搭成的一个几何体,它的主视图是( )
A. B. C. D.
5.(3分)(2021秋•南阳期末)已知am=5,an=2,则a2m+n的值等于( )
A.50 B.27 C.12 D.25
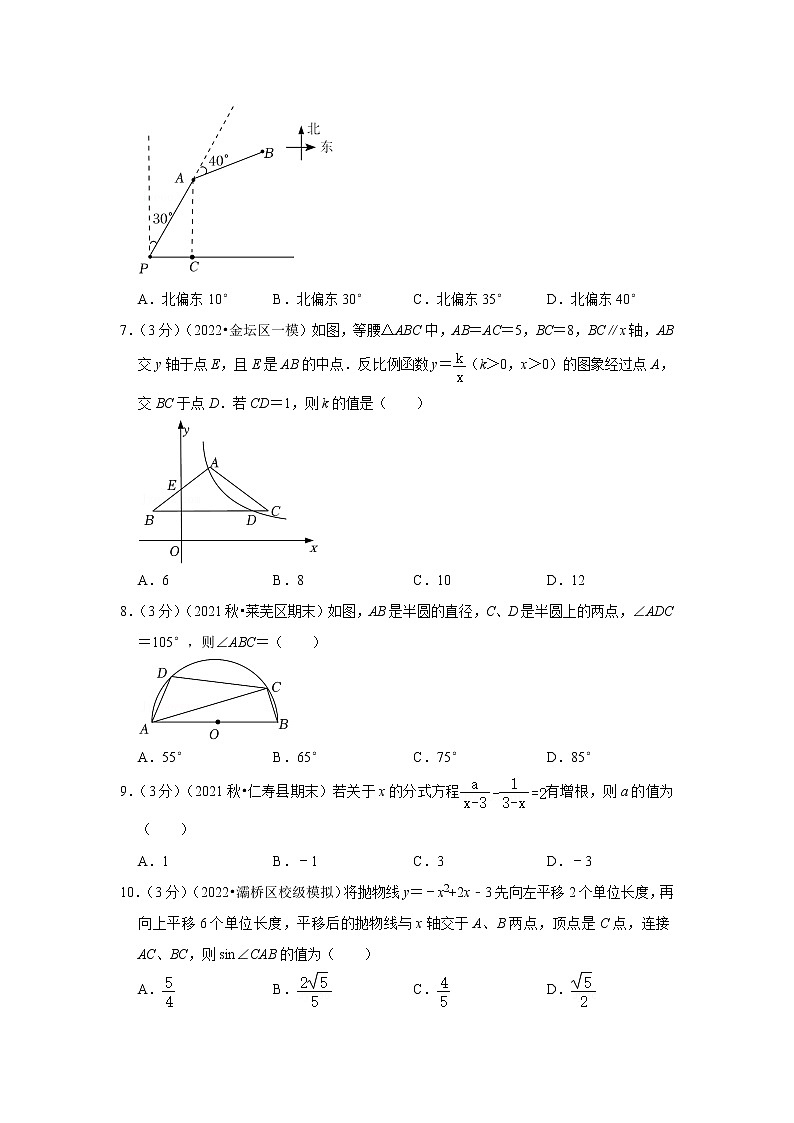
6.(3分)(2022•景县校级模拟)如图,某渔船正在海上P处捕鱼,先向北偏东30°的方向航行10km到A处,然后右转40°再航行到B处.在点A的正南方向,点P的正东方向的C处有一条船,也计划驶往B处,那么它的航向是( )
A.北偏东10° B.北偏东30° C.北偏东35° D.北偏东40°
7.(3分)(2022•金坛区一模)如图,等腰△ABC中,AB=AC=5,BC=8,BC∥x轴,AB交y轴于点E,且E是AB的中点.反比例函数y=(k>0,x>0)的图象经过点A,交BC于点D.若CD=1,则k的值是( )
A.6 B.8 C.10 D.12
8.(3分)(2021秋•莱芜区期末)如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=105°,则∠ABC=( )
A.55° B.65° C.75° D.85°
9.(3分)(2021秋•仁寿县期末)若关于x的分式方程有增根,则a的值为( )
A.1 B.﹣1 C.3 D.﹣3
10.(3分)(2022•灞桥区校级模拟)将抛物线y=﹣x2+2x﹣3先向左平移2个单位长度,再向上平移6个单位长度,平移后的抛物线与x轴交于A、B两点,顶点是C点,连接AC、BC,则sin∠CAB的值为( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2021秋•河西区期末)中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口约为4500000000人,这个数用科学记数法表示为 .
12.(3分)(2022•凤山县模拟)的平方根是 .
13.(3分)(2021秋•正定县期末)如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=3,则阴影部分周长的最小值为 .
14.(3分)(2021秋•广丰区期末)已知点M(2.0),⊙M的半径为1,OA切⊙M于点A,点P为⊙M上的动点,当P的坐标为 时,△POA是等腰三角形.
15.(3分)(2022•铁西区一模)一元一次不等式组的整数解的个数是 .
16.(3分)(2021秋•玄武区校级期末)如图,在△ABC中,AB=AC,AD是△ABC的角平分线,E是AC中点,连接DE,若DE=3,则AB= .
三.解答题(共9小题,满分72分)
17.(4分)(2021秋•济南期末)计算:.
18.(4分)(2021秋•建湖县期末)如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC.
求证:(1)△ACE≌△BCD;
(2)AE⊥BD.
19.(6分)(2021秋•东台市期末)如图,一次函数y=2xm﹣1﹣1与y轴交于点C,点A的坐标为(m,3).
(1)试判断点A是否在此函数图象上;
(2)若P为y轴上一点,且△APC的面积为6,求点P的坐标.
20.(6分)(2022春•义乌市校级月考)北京时间2021年12月9日15时40分,“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年带来了一场精彩的太空科普课.为引导同学们学习天文知识、探索宇宙奥秘,学校组织了太空知识竞赛,如表是小宇同学初赛和复赛的成绩(单位:分).
场次
初赛
复赛
第一场
第二场
第三场
第四场
第一场
第二场
小宇
88
92
90
86
90
96
(1)小宇同学这6场比赛成绩的中位数是 分,众数是 分;
(2)在决赛现场,小宇和小航角逐冠亚军,他们在基础关、提高关、挑战关的得分如表所示(单位:分).按照规定,决赛按照基础、提高、挑战三个环节2:3:5的比例计算最终成绩,请通过计算说明小宇和小航谁将获胜.
姓名
基础关
提高关
挑战关
小宇
80
90
85
小航
95
85
80
21.(8分)(2021秋•阜宁县期末)定义新运算:对于任意实数m,n都有m★n=m2n+n,等式右边是常用的加法、减法、乘法及乘方运算.例如:﹣3★2=(﹣3)2×2+2=20.根据以上知识解决问题:
(1)若(x+1)★3=15,求x的值.
(2)若2★a的值小于0,请判断关于x的方程:2x2﹣bx+a=0的根的情况.
22.(10分)(2020•浙江自主招生)如图,扇形AOB中,记扇形所在圆的半径OA=r,并记弧AB长为l,即=l.
(1)求扇形AOB的面积S(用r,l表示);
(2)已知扇形AOB的周长为定值π,即2r+l=π,求扇形AOB的面积S的最大值,并求当S取最大值时,的值.
23.(10分)(2021秋•亳州期末)某裁缝店在线上以45元套的价格接了一批制作篮球服的业务,该裁缝店每天制作篮球服的数量x(套)满足20≤x≤50,且每件篮球服制作成本y(元)与每天制作篮球服的数量x(套)之间的函数关系满足:y=﹣x+50,若该裁缝店每天消耗的其他成本为200元,每天的利润为w元.
(1)求w与x之间的函数表达式;
(2)每天生产多少套时,每天的利润w有最大值?最大利润是多少?
24.(12分)(2022春•义乌市期中)(1)如图1,将长方形纸片ABFE沿着线段DC折叠,CF交AD于点H,过点H作HG∥DC,交线段CB于点G.
①判断∠FHG与∠EDC是否相等,并说明理由;
②说明HG平分∠AHC的理由.
(2)如图2,如果将(1)中的已知条件改为折叠三角形纸片ABE,其它条件不变,HG是否平分∠AHC?如果平分请说明理由;如果不平分,请找出∠CHG,∠AHG与∠E的数量关系说明理由.
25.(12分)(2022•平遥县一模)如图,在平面直角坐标系中,四边形ABCD为正方形,点A,B在x轴上,抛物线y=x2+bx+c经过点B,D(﹣4,5)两点,且与直线DC交于一点E.
(1)求抛物线的解析式;
(2)若点P为y轴上一点,探究EP+PB是否存在最小值.若存在,请求出这个最小值及点P的坐标;若不存在,请说明理由;
(3)若点F为抛物线对称轴上一点,点Q为平面直角坐标系中的一点,是否存在以点Q,F,E,B为顶点的四边形是以BE为边的菱形.若存在,请求出点F的坐标;若不存在,请说明理由.
2022年广州中考数学终极押题密卷2
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)下列各组数中,互为相反数的是( )
A.6和﹣6 B.﹣6和 C.﹣6和 D.和6
【考点】相反数.
【专题】实数;运算能力.
【分析】相反数定义:数值相反的两个数,其中一个数是另一个数的相反数.由此可求解.
【解答】解:A.6和﹣6互为相反数,符合题意;
B.﹣6和互为负倒数,不符合题意;
C.﹣6和﹣互为倒数,不符合题意;
D.6和互为倒数,不符合题意;
故选:A.
【点评】本题考查相反数,熟练掌握相反数的定义是解题的关键.
2.(3分)(2021秋•八公山区期末)下列图案是几种名车的标志,请你指出,在这几个图案中是轴对称图形的共有( )
A.1个 B.2个 C.3个 D.4个
【考点】轴对称图形.
【分析】关于某条直线对称的图形叫轴对称图形.绕一个点旋转180度后所得的图形与原图形完全重合的图形叫做中心对称图形.
【解答】解:第一个是中心对称图形,但不是轴对称图形,其它三个是轴对称图形.故选C.
【点评】轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
3.(3分)(2022春•宁海县期中)一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示.若每双鞋的销售利润相同,则该店主最应关注的销售数据是下列统计量中的( )
鞋的尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量双
1
2
5
11
7
3
1
A.平均数 B.方差 C.众数 D.中位数
【考点】统计量的选择;算术平均数;中位数;众数;方差.
【专题】统计的应用;数据分析观念.
【分析】根据题意,联系商家最关注的应该是最畅销的鞋码,则考虑该店主最应关注的销售数据是众数.
【解答】解:因为众数是在一组数据中出现次数最多的数,
又根据题意,每双鞋的销售利润相同,鞋店为销售额考虑,应关注卖出最多的鞋子的尺码,这样可以确定进货的数量,
所以该店主最应关注的销售数据是众数.
故选:C.
【点评】本题主要考查数据的收集和处理.解题关键是熟悉统计数据的意义,并结合实际情况进行分析.根据众数是在一组数据中出现次数最多的数,再联系商家最关注的应该是最畅销的鞋码,则考虑该店主最应关注的销售数据是众数.
4.(3分)(2022•滨海新区一模)如图是由几个相同的正方体搭成的一个几何体,它的主视图是( )
A. B. C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
【解答】解:从正面看,易得:底层有三个正方形,上层中间是一个小正方形.
故选:D.
【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
5.(3分)(2021秋•南阳期末)已知am=5,an=2,则a2m+n的值等于( )
A.50 B.27 C.12 D.25
【考点】幂的乘方与积的乘方;同底数幂的乘法.
【专题】常规题型.
【分析】直接利用同底数幂的乘除运算法则以及幂的乘方运算法则分别计算得出答案.
【解答】解:∵am=5,an=2,
∴a2m+n=(am)2×an
=52×2
=50.
故选:A.
【点评】此题主要考查了同底数幂的乘除运算以及幂的乘方运算,正确掌握运算法则是解题关键.
6.(3分)(2022•景县校级模拟)如图,某渔船正在海上P处捕鱼,先向北偏东30°的方向航行10km到A处,然后右转40°再航行到B处.在点A的正南方向,点P的正东方向的C处有一条船,也计划驶往B处,那么它的航向是( )
A.北偏东10° B.北偏东30° C.北偏东35° D.北偏东40°
【考点】解直角三角形的应用﹣方向角问题.
【专题】等腰三角形与直角三角形;解直角三角形及其应用;运算能力;推理能力;应用意识.
【分析】连接BC,由锐角三角函数定义得AC=PA=5(km),则AC=AB,再由等腰三角形的性质得∠ACB=∠ABC=35°,即可得出结论.
【解答】解:如图,连接BC,
由题意得:∠ACP=∠ACD=90°,∠PAC=30°,PA=10km,∠BAE=40°,AB=,
∴∠BAC=180°﹣∠PAC﹣∠BAE=180°﹣30°﹣40°=110°,
∵cos∠PAC==cos30°=,
∴AC=PA=×10=5(km),
∴AC=AB,
∴∠ACB=∠ABC=×(180°﹣∠BAC)=×(180°﹣110°)=35°,
即B处在C处的北偏东35°方向,
故选:C.
【点评】本题考查了解直角三角形的应用—方向角问题,等腰三角形的性质,锐角三角函数定义等知识,由锐角三角函数定义求出AC的长是解题的关键.
7.(3分)(2022•金坛区一模)如图,等腰△ABC中,AB=AC=5,BC=8,BC∥x轴,AB交y轴于点E,且E是AB的中点.反比例函数y=(k>0,x>0)的图象经过点A,交BC于点D.若CD=1,则k的值是( )
A.6 B.8 C.10 D.12
【考点】反比例函数图象上点的坐标特征;等腰三角形的性质.
【专题】反比例函数及其应用;等腰三角形与直角三角形;运算能力.
【分析】过A作AM⊥BC于M交x轴于N,则AM∥y轴,根据勾股定理得到AM=3,设D点的坐标为(5,m),则A(2,m+3),即可得到k=5m=2(m+3),解方程求得M的值,进而求得k的值.
【解答】解:过A作AM⊥BC于M,交x轴于N,
∵AB=AC=5,BC=8,
∴BM=CM=BC=4,
∴AM===3,
∵AM∥y轴,E是AB的中点,
∴ON=×4=2,
∴M的横坐标为2,C的横坐标为6,
∴CD=1,
∴D的横坐标为5,
设D点的坐标为(5,m),则A(2,m+3),
∵反比例函数y=(k>0,x>0)的图象经过点A,交BC于点D.
∴k=5m=2(m+3),
解得:m=2,
∴k=5×2=10,
故选:C.
【点评】本题考查了反比例函数图象上点的坐标特征,等腰三角形的性质,勾股定理,表示出点的坐标是解题的关键.
8.(3分)(2021秋•莱芜区期末)如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=105°,则∠ABC=( )
A.55° B.65° C.75° D.85°
【考点】圆周角定理.
【专题】与圆有关的计算;几何直观.
【分析】连接BD,先根据圆周角定理得到∠ADB=90°,则可计算出∠BDC=15°,然后根据圆周角定理得到∠CAB的度数进而求出答案.
【解答】解:连接BD,如图,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠BDC=∠ADC﹣∠ADB=105°﹣90°=15°,
∴∠CAB=∠BDC=15°.
∴∠ABC=90°﹣∠CAB=75°.
故选:C.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
9.(3分)(2021秋•仁寿县期末)若关于x的分式方程有增根,则a的值为( )
A.1 B.﹣1 C.3 D.﹣3
【考点】分式方程的增根.
【专题】分式方程及应用;运算能力.
【分析】首先把所给的分式方程化为整式方程,然后根据分式方程有增根,得到x﹣3=0,据此求出x的值,代入整式方程求出a的值即可.
【解答】解:去分母,得:a+1=2(x﹣3),
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程,可得:a=﹣1.
故选:B.
【点评】此题主要考查了分式方程的增根,解答此题的关键是要明确:(1)化分式方程为整式方程;(2)把增根代入整式方程即可求得相关字母的值.
10.(3分)(2022•灞桥区校级模拟)将抛物线y=﹣x2+2x﹣3先向左平移2个单位长度,再向上平移6个单位长度,平移后的抛物线与x轴交于A、B两点,顶点是C点,连接AC、BC,则sin∠CAB的值为( )
A. B. C. D.
【考点】抛物线与x轴的交点;解直角三角形;二次函数的性质;二次函数图象与几何变换.
【专题】二次函数图象及其性质;运算能力;推理能力.
【分析】先求得平移后的抛物线解析式,然后求得点A、B、C的坐标,进而求得sin∠CAB的值.
【解答】解:∵抛物线y=﹣x2+2x﹣3先向左平移2个单位长度,再向上平移6个单位长度,
∴平移后的解析式为y=﹣(x+2)2+2(x+2)﹣3+6=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点C的坐标为(﹣1,4),
令y=0,得﹣x2﹣2x+3=0,
解得:x=﹣3或x=1,
∴点A(﹣3,0),B(1,0),
∴AC==2,
∴sin∠CAB=,
故选:B.
【点评】本题考查了二次函数的平移变换,二次函数图象上点的特征,解直角三角形解题的关键是能够求得平移后的函数解析式.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)(2021秋•河西区期末)中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口约为4500000000人,这个数用科学记数法表示为 4.5×109 .
【考点】科学记数法—表示较大的数.
【专题】实数;数感.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:4500000000=4.5×109.
故答案为:4.5×109.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
12.(3分)(2022•凤山县模拟)的平方根是 ±2 .
【考点】算术平方根;平方根.
【专题】实数;运算能力.
【分析】先计算=4,再根据平方根的性质可得4的平方根是±2.
【解答】解:∵=4,
∴的平方根是±2.
故答案为:±2.
【点评】本题考查了算术平方根和平方根,掌握算术平方根和平方根的定义,根据定义计算是解题关键.
13.(3分)(2021秋•正定县期末)如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=3,则阴影部分周长的最小值为 3+ .
【考点】弧长的计算;圆周角定理.
【专题】与圆有关的计算;应用意识.
【分析】利用轴对称的性质,得出当点E移动到点E′时,阴影部分的周长最小,此时的最小值为弧CD的长与CD′的长度和,分别进行计算即可.
【解答】解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′.
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===3,
∴的长l==,
∴阴影部分周长的最小值为3+.
故答案为:3+.
【点评】本题考查与圆有关的计算,掌握轴对称的性质,弧长的计算方法是正确计算的前提,理解轴对称解决路程最短问题是关键.
14.(3分)(2021秋•广丰区期末)已知点M(2.0),⊙M的半径为1,OA切⊙M于点A,点P为⊙M上的动点,当P的坐标为 (1,0),(3,0)(,) 时,△POA是等腰三角形.
【考点】切线的性质;坐标与图形性质;等腰三角形的判定;勾股定理.
【专题】推理填空题;平面直角坐标系;等腰三角形与直角三角形;与圆有关的位置关系;运算能力;推理能力.
【分析】根据题意画出图形分三种情况讨论:当点P在x轴上,PA=PO=1,OA=OP″=3,当点P是切点时,AO=AP=,进而可以解决问题.
【解答】解:如图,当P的坐标为(1,0),(3,0),(,)时,△POA是等腰三角形.理由如下:
连接AM,
∵M(2.0),⊙M的半径为1,
∴OM=2,AM=PM=1,
∴OP=1,
∵OA切⊙M于点A,
∴∠MAO=90°,
∴∠AOM=30°,
∴∠AMO=60°,
∴PA=AM=PM=1,
∴OP=PA=1,
∴P(1,0);
当OA=OP′时,连接AP′交x轴于点H,
∵OA切⊙M于点A,
∴OP′切⊙M于点P′,
∴∠P′OM=∠AOM=30°,
∴∠AOP′=60°,
∴△AOP′是等边三角形,
∴AP′=OA===,
∴OH=OA=,P′H=AP′=,
∴P′(,);
∵MA=MP″,∠AMO=60°,
∴∠MAP″=∠MP″A=30°,
∴∠AOP″=∠MP″A=30°,
∴OA=OP″,
∴P″(3,0).
综上所述:当P的坐标为(1,0),(3,0),(,)时,△POA是等腰三角形.
故答案为:(1,0),(3,0),(,).
【点评】本题考查了切线的性质,等腰三角形的判定与性质,勾股定理,等边三角形的判定与性质,坐标与图形性质,解决本题的关键是得到△AOP′是等边三角形.
15.(3分)(2022•铁西区一模)一元一次不等式组的整数解的个数是 6 .
【考点】一元一次不等式组的整数解.
【分析】先求出不等式的解集,再求出不等式组的解集,找出不等式组的整数解即可.
【解答】解:∵解不等式2x+1>0得:x>﹣,
解不等式x﹣5≤0得:x≤5,
∴不等式组的解集是﹣<x≤5,
整数解为0,1,2,3,4,5,共6个,
故答案为6.
【点评】本题考查了解一元一次不等式,解一元一次不等式组的应用,解此题的关键是求出不等式组的解集.
16.(3分)(2021秋•玄武区校级期末)如图,在△ABC中,AB=AC,AD是△ABC的角平分线,E是AC中点,连接DE,若DE=3,则AB= 6 .
【考点】三角形中位线定理;角平分线的性质;等腰三角形的性质;直角三角形斜边上的中线.
【专题】三角形;推理能力.
【分析】根据等腰三角形的三线合一得到BD=DC,根据三角形中位线定理解答即可.
【解答】解:∵AB=AC,AD是△ABC的角平分线,
∴BD=DC,
∵E是AC中点,
∴DE是△ABC的中位线,
∴AB=2DE=2×3=6,
故答案为:6.
【点评】本题考查的是三角形中位线定理、等腰三角形的性质,三角形的中位线平行于第三边,且等于第三边的一半.
三.解答题(共9小题,满分72分)
17.(4分)(2021秋•济南期末)计算:.
【考点】实数的运算.
【专题】实数;运算能力.
【分析】直接利用绝对值的性质和二次根式的性质、立方根的性质分别化简,进而利用实数的加减运算法则计算得出答案.
【解答】解:原式=+3﹣3+12
=+12.
【点评】此题主要考查了绝对值的性质和二次根式的性质、立方根的性质,正确化简各数是解题关键.
18.(4分)(2021秋•建湖县期末)如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC.
求证:(1)△ACE≌△BCD;
(2)AE⊥BD.
【考点】全等三角形的判定与性质;等腰直角三角形.
【专题】图形的全等;等腰三角形与直角三角形;推理能力.
【分析】(1)由垂直的定义得到∠ACB=∠DCE=90°,即得出∠ECA=∠DCB,即可利用SAS证明△DCB≌△ECA;
(2)由(1)得到∠A=∠B,由∠AGD=∠BGC,∠B+∠BGC=90°推出∠A+∠AGD=90°,可得∠AFG=90°,即可解决问题.
【解答】(1)证明:∵AC⊥BC,DC⊥EC,
∴∠ACB=∠DCE=90°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ECA=∠DCB,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS);
(2)证明:如图,AC与BD相交于点G,AE与BD相交于点F,
由(1)知,△ACE≌△BCD,
∴∠A=∠B,
∵∠AGD=∠BGC,∠B+∠BGC=90°,
∴∠A+∠AGD=90°,
∴∠AFG=180°﹣90°=90°,
∴AE⊥BD.
【点评】本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
19.(6分)(2021秋•东台市期末)如图,一次函数y=2xm﹣1﹣1与y轴交于点C,点A的坐标为(m,3).
(1)试判断点A是否在此函数图象上;
(2)若P为y轴上一点,且△APC的面积为6,求点P的坐标.
【考点】一次函数图象上点的坐标特征;一次函数的性质.
【专题】一次函数及其应用;运算能力.
【分析】(1)根据一次函数的定义可得m=2,把点A的坐标分别代入函数的解析式,看看两边是否相等即可;
(2)根据△APC的面积为6,求得PC的长度,进而求出点P的坐标即可.
【解答】解:(1)∵y=2xm﹣1﹣1是一次函数,
∴m﹣1=1,解得m=2,
∴点A的坐标为(2,3),
∴把A点的坐标代入y=2x﹣1,左边=3,右边=2×2﹣1=3,左边=右边,
∴点A(2,3)在此函数的图象上;
(2)把x=0代入y=2x﹣1得:y=﹣1,
即点C的坐标为(0,﹣1),
∵点P是y轴上一点,且△APC的面积为6,
∴×PC×2=6,
∴PC=6,
∵点C的坐标为(0,﹣1),
∴点P 的坐标为(0,5)或(0,﹣7).
【点评】本题考查了一次函数图象上点的坐标特征,一次函数的性质,三角形的面积,能理解函数图象上点的坐标的特点是解此题的关键
20.(6分)(2022春•义乌市校级月考)北京时间2021年12月9日15时40分,“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年带来了一场精彩的太空科普课.为引导同学们学习天文知识、探索宇宙奥秘,学校组织了太空知识竞赛,如表是小宇同学初赛和复赛的成绩(单位:分).
场次
初赛
复赛
第一场
第二场
第三场
第四场
第一场
第二场
小宇
88
92
90
86
90
96
(1)小宇同学这6场比赛成绩的中位数是 90 分,众数是 90 分;
(2)在决赛现场,小宇和小航角逐冠亚军,他们在基础关、提高关、挑战关的得分如表所示(单位:分).按照规定,决赛按照基础、提高、挑战三个环节2:3:5的比例计算最终成绩,请通过计算说明小宇和小航谁将获胜.
姓名
基础关
提高关
挑战关
小宇
80
90
85
小航
95
85
80
【考点】扇形统计图;加权平均数;中位数;众数.
【专题】统计的应用;运算能力.
【分析】(1)根据中位数、众数的定义进行解答即可;
(2)根据加权平均数的计算方法计算小宇、小航的平均数即可.
【解答】解:(1)将这6次比赛成绩从小到大排列后,处在中间位置的两个数都是90分,因此中位数是90分,
小宇这6场比赛成绩出现次数最多的是90分,因此众数是90分,
故答案为:90,90;
(2)小宇获胜,理由为:
小宇的平均分为:80×+90×+85×=85.5(分),
小航的平均分为:95×+85×+80×=84.5(分),
∵85.5>84.5,
∴小宇获胜.
【点评】本题考查中位数、众数以及加权平均数,掌握中位数、众数以及加权平均数的计算方法是正确解答的关键.
21.(8分)(2021秋•阜宁县期末)定义新运算:对于任意实数m,n都有m★n=m2n+n,等式右边是常用的加法、减法、乘法及乘方运算.例如:﹣3★2=(﹣3)2×2+2=20.根据以上知识解决问题:
(1)若(x+1)★3=15,求x的值.
(2)若2★a的值小于0,请判断关于x的方程:2x2﹣bx+a=0的根的情况.
【考点】根的判别式;解一元一次不等式;实数的运算;一元一次方程的解.
【专题】一元二次方程及应用;运算能力.
【分析】(1)根据新运算得出3(x+1)2+3=15,解之可得到答案;
(2)由2★a的值小于0知22a+a=5a<0,解之求得a<0.再在方程2x2﹣bx+a=0中由Δ=(﹣b)2﹣8a≥﹣8a>0可得答案.
【解答】解:(1)∵(x+1)★3=15,
∴3(x+1)2+3=15,即(x+1)2=4,
解得:x1=1,x2=﹣3;
(2)∵2★a的值小于0,
∴22a+a=5a<0,
解得:a<0.
在方程2x2﹣bx+a=0中,
∵Δ=(﹣b)2﹣8a≥﹣8a>0,
∴方程2x2﹣bx+a=0有两个不相等的实数根.
【点评】本题主要考查根的判别式,一元二次方程的解法,实数的运算,解一元一次不等式,正确理解新运算是解决问题的关键.
22.(10分)(2020•浙江自主招生)如图,扇形AOB中,记扇形所在圆的半径OA=r,并记弧AB长为l,即=l.
(1)求扇形AOB的面积S(用r,l表示);
(2)已知扇形AOB的周长为定值π,即2r+l=π,求扇形AOB的面积S的最大值,并求当S取最大值时,的值.
【考点】扇形面积的计算;弧长的计算.
【专题】与圆有关的计算;运算能力.
【分析】(1)设∠AOB=α,根据扇形的面积公式即可得到结论;
(2)由已知条件得到l=π﹣2r,求得S=﹣(r﹣)2+,根据二次函数的性质即可得到结论.
【解答】解:(1)设∠AOB=α,则2πr=l,
∴=,
∴S=πr2•=;
(2)∵2r+l=π,
∴l=π﹣2r,
∴S===﹣(r﹣)2+,
当r=时,S最大=,
此时,l=,=2.
【点评】本题考查了扇形面积的计算,弧长的计算,正确的理解题意是解题的关键.
23.(10分)(2021秋•亳州期末)某裁缝店在线上以45元套的价格接了一批制作篮球服的业务,该裁缝店每天制作篮球服的数量x(套)满足20≤x≤50,且每件篮球服制作成本y(元)与每天制作篮球服的数量x(套)之间的函数关系满足:y=﹣x+50,若该裁缝店每天消耗的其他成本为200元,每天的利润为w元.
(1)求w与x之间的函数表达式;
(2)每天生产多少套时,每天的利润w有最大值?最大利润是多少?
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【分析】(1)根据利润=(45﹣成本)×数量﹣其他成本,列出函数解析式即可;
(2)根据自变量的取值范围由函数的性质求最值即可.
【解答】解:(1)由题意得:w=(45﹣y)x﹣200
=[45﹣(﹣x+50)]x﹣200
=x2﹣5x﹣200,
∴w与x之间的函数表达式w=x2﹣5x﹣200;
(2)w=x2﹣5x﹣200=(x﹣5)2﹣212.5,
∵>0,抛物线的对称轴为直线x=5,
∴当x>5时,w随x的增大而增大,
又∵20≤x≤50,
∴当x=50时,w有最大值,最大值为800,
∴每天生产50套时,每天的利润w有最大值,最大利润是800元.
【点评】本题考查二次函数的应用,关键是找到等量关系列出函数解析式.
24.(12分)(2022春•义乌市期中)(1)如图1,将长方形纸片ABFE沿着线段DC折叠,CF交AD于点H,过点H作HG∥DC,交线段CB于点G.
①判断∠FHG与∠EDC是否相等,并说明理由;
②说明HG平分∠AHC的理由.
(2)如图2,如果将(1)中的已知条件改为折叠三角形纸片ABE,其它条件不变,HG是否平分∠AHC?如果平分请说明理由;如果不平分,请找出∠CHG,∠AHG与∠E的数量关系说明理由.
【考点】四边形综合题.
【专题】几何综合题;应用意识.
【分析】(1)①如图1中,结论:∠FHG=∠EDC.利用平行线的性质解决问题即可.
②利用翻折不变性,平行线的性质解决问题即可.
(2)如图2中,结论:HG不平分∠AHC,∠AHG=∠CHG+∠E.利用三角形的外角的性质以及平行线的性质解决问题即可.
【解答】(1)①解:如图1中,结论:∠FHG=∠EDC.
理由:∵HG∥CD,
∴∠AHG=∠ADC,
∵DE∥CF,
∴∠AHF=∠ADE,
∵∠FHG=∠AHF+∠AHG,∠EDC=∠ADE+∠ADC,
∴∠FHG=∠EDC.
②证明:
∵HG∥CD,
∴∠2=∠3,
∵AD∥BC,
∴∠3+∠4=∠1+∠2,
由翻折可知∠1=∠2,
∴∠3+∠4=2∠2,
∵∠2=∠3,
∴∠3=∠4,
∴HG平分∠AHC.
(2)如图2中,结论:HG不平分∠AHC,∠AHG=∠CHG+∠E.
理由:延长AD交BC的延长线于E′.
由翻折可知∠E=∠E′,∠ECD=∠E′CD,
∵GH∥DC,
∴∠AHG=∠ADC,∠CHG=∠ECD=∠E′CD,
∵∠ADC=∠E′+∠E′CD,
∴∠AHG=∠E+∠CHG.
【点评】本题属于四边形综合题,考查了翻折变换,平行线的性质,三角形的外角的性质,角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
25.(12分)(2022•平遥县一模)如图,在平面直角坐标系中,四边形ABCD为正方形,点A,B在x轴上,抛物线y=x2+bx+c经过点B,D(﹣4,5)两点,且与直线DC交于一点E.
(1)求抛物线的解析式;
(2)若点P为y轴上一点,探究EP+PB是否存在最小值.若存在,请求出这个最小值及点P的坐标;若不存在,请说明理由;
(3)若点F为抛物线对称轴上一点,点Q为平面直角坐标系中的一点,是否存在以点Q,F,E,B为顶点的四边形是以BE为边的菱形.若存在,请求出点F的坐标;若不存在,请说明理由.
【考点】二次函数综合题.
【专题】代数几何综合题;压轴题;运算能力;推理能力;应用意识.
【分析】(1)运用待定系数法即可求得答案;
(2)作点E关于y轴对称点为E',连接BE′交y轴于点P,则EP+PB=E′P+PB=E′B=为最小值,利用待定系数法求得直线BE'的表达式为y=﹣x+,令x=0,即可求得点P的坐标;
(3)以点Q,F,E,B为顶点的四边形是以BE为边的菱形,则BE=BF或BE=EF,分两种情况分别建立方程求解即可得出答案.
【解答】解:(1)由点D的纵坐标知,正方形ABCD的边长为5,
则OB=AB﹣AO=5﹣4=1,故点B的坐标为(1,0),
则,
解得,
∴抛物线的表达式为y=x2+2x﹣3;
(2)EP+PB存在最小值,理由如下:
∵点E关于y轴对称点为E',且点E的坐标为(2,5),
∴点E'坐标为(﹣2,5).
连接BE',交y轴于点P,连接EP,则此时EP+PB=E′P+PB=E′B最小,
由点B的坐标为(1,0),点E'坐标为(﹣2,5)
设直线BE′的函数表达式为y=kx+d,
则,
解得:,
∴直线BE'的表达式为y=﹣x+,
令x=0,得y=,
∴点P坐标为.
在Rt△BCE′中,BC=5,CE′=1﹣(﹣2)=3,
∴BE′===,
则EP+PB的最小值=BE′=.
(3)∵y=x2+2x﹣3=(x+1)2﹣4,
∴抛物线对称轴为直线x=﹣1,设点F的坐标为(﹣1,m),
在Rt△BCE中,BC=5,CE=1,∠BCE=90°,
∴BE2=BC2+CE2=52+12=26,
∵以点Q,F,E,B为顶点的四边形是以BE为边的菱形,
∴BE=BF或BE=EF,
当BE=BF时,如图2,设直线x=﹣1与x轴交于点H,则H(﹣1,0),
∴BH=1﹣(﹣1)=2,HF=|m|,
∴BF2=BH2+HF2=22+|m|2=4+m2,
∴4+m2=26,
解得:m1=,m2=﹣;
当EB=EF时,如图3,设直线x=﹣1与CD交于点K,则K(﹣1,5),
∴EK=2﹣(﹣1)=3,KF=|m﹣5|,
在Rt△EKF中,EF2=EK2+KF2=32+|m﹣5|2=m2﹣10m+34,
∴m2﹣10m+34=26,
解得:m3=5+,m4=5﹣;
故点F的坐标为或或或.
【点评】本题是二次函数综合题,考查了待定系数法求函数解析式,利用轴对称求最短路径,菱形的性质,勾股定理等,难度适中,运用分类讨论思想和数形结合思想是解题关键
相关试卷
这是一份2022年南京中考数学终极押题密卷2,共36页。试卷主要包含了计算,+1的结果是 等内容,欢迎下载使用。
这是一份2022年杭州中考数学终极押题密卷2,共27页。
这是一份2022年哈尔滨中考数学终极押题密卷2,共32页。








