专题06 双垂直型-九年级数学相似三角形基本模型探究（北师大版）

专题06 双垂直型

【基本模型】

①如图，直角三角形被斜边上的高分成的两个直角三角形与原三角形相似，即△ACD∽△ABC∽△CBD.常见的结论有：CA2＝AD·AB，BC2＝BD·BA，CD2＝DA·DB.

②拓展：

（1）正方形、长方形中经常会出现射影定理模型，如图，在和内均有射影定理模型．

（2）如图，在圆中也会出现射影定理模型．

【例题精讲】

例1.如图，AD∥BC，AE平分∠DAB，BE平分∠ABC，EF⊥AB．证明：△AEF∽△ABE．

【答案】见解析．

【详解】证明：∵AE平分∠DAB，BE平分∠ABC，

∴∠BAE＝∠DAB，∠ABE＝∠ABC.

∵AD∥BC，∴∠DAB＋∠ABC＝180°，

∴∠BAE＋∠ABE＝90°，∴∠AEB＝90°.

∵EF⊥AB，∴∠AFE＝90°.

又∵∠BAE＝∠EAF，∴△AEF∽△ABE

例2.如图所示，在△ABC中，∠ABC＝90°，BD⊥AC，DE⊥BC，垂足分别为D、E两点，则图中与△ABC相似的三角形有（　　）

A．4个 B．3个 C．2个 D．1个

【解析】∵在△ABC中，∠ABC＝90°，BD⊥AC，DE⊥BC，

∴∠A＝∠EBD＝∠CDE，∴△ADB∽△BED∽△DEC∽△BDC∽△ABC，

∴共有四个三角形与Rt△ABC相似．故选：A．

例3.如图，四边形ABCD中，AD∥BC，∠B＝90°，E为AB上一点，分别以ED、EC为折痕将

两个角(∠A、∠B)向内折起，点A、B恰好落在CD边的点F处，若AD＝3，BC＝5，则EF的长是（   ）

A.      B．2       C.                 D．2

【解析】∵AD∥BC，∴∠ADF＋∠FCB＝180°.

根据折叠前后的图形全等得到DF＝DA＝3，

∠ADE＝∠FDE，CF＝CB＝5，∠BCE＝∠FCE，∠EFC＝∠B＝90°，

∴∠FDE＋∠FCE＝90°，∠FCE＋∠FEC＝90°，

∠DFE＝∠EFC＝90°，∴∠FDE＝∠FEC，

∴△DEF∽△ECF，∴＝，

∴EF2＝DF·CF＝3×5＝15，∴EF＝.故选A.

【变式训练1】如图，在中，，是边上的高．

（1）若，则________；

（2）若，则________；

（3）若，则________．

【答案】    ①. 4    ②.     ③.

【详解】解：（1）∵在中，，是边上的高．

∴∠ADC=∠ACB=90°，又∠A=∠A，

∴△ADC∽△ACB，

∴ ，即，

解得：AD= 4，

故答案为：4；

（2）由（1）知△ADC∽△ACB，

∴ ，即，

解得：AD=2，或AD=﹣8（舍去），

在Rt△ADC中，由勾股定理得：CD=，

故答案为：；

（3）在Rt△ADC中，AC=5，CD=4，

由勾股定理得：AD= ，

由（1）中△ADC∽△ACB，

∴ ，即，解得：BC= ，

经检验，BC= ，故答案为：．

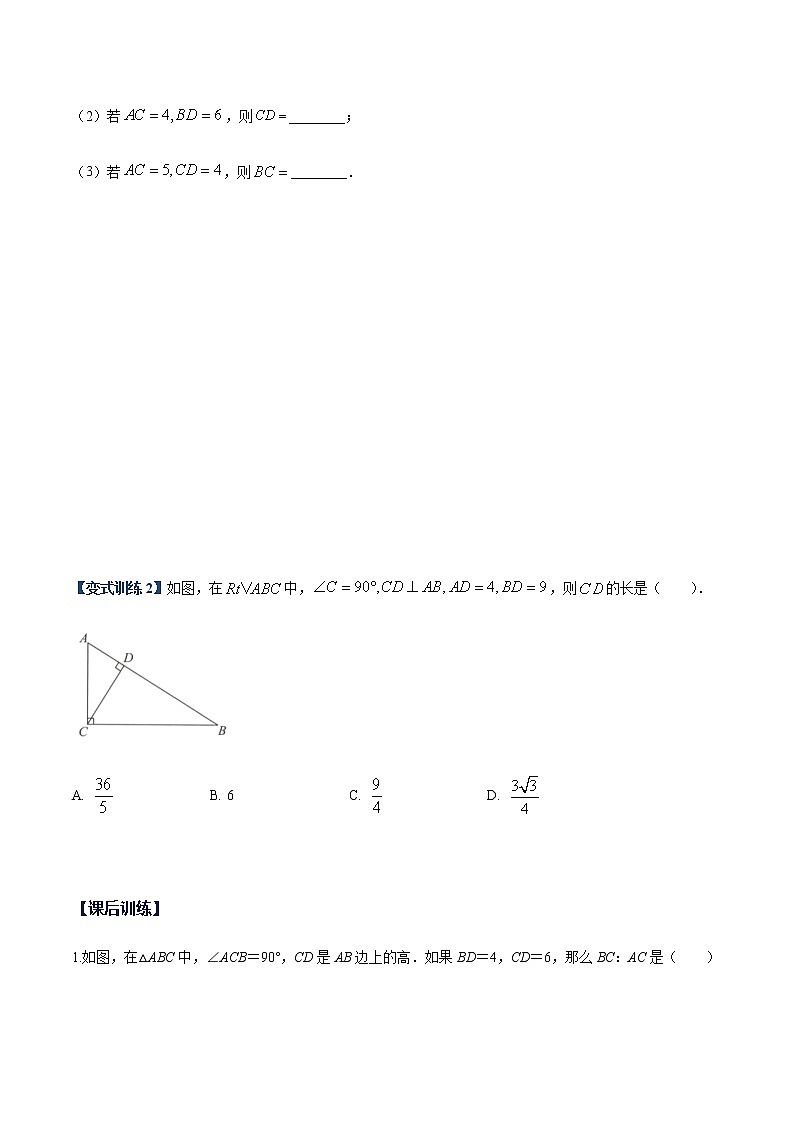
【变式训练2】如图，在中，，则的长是（    ）．

A.  B. 6 C.  D.

【答案】B

【详解】解：∵如图，在Rt△ABC中，∠C＝90°，CD⊥AB，

∴∠A+∠ACD=∠ACD+∠BCD=90°，∴∠A=∠BCD，

又∵∠ADC=∠CDB=90°，

∴，∴，

∴CD2＝BD•AD=9×4＝36，

∴CD＝6（舍去负值）．

故选：B．

【课后训练】

1.如图，在△ABC中，∠ACB＝90°，CD是AB边上的高．如果BD＝4，CD＝6，那么BC：AC是（　　）

A．3：2 B．2：3 C． D．．

【解析】∵∠ACB＝90°，CD是AB边上的高，

∴∠ADC＝∠CDB＝∠ACB＝90°，

∵∠A+∠B＝90°，∠A+∠ACD＝90°，

∴∠ACD＝∠B，∴△ACD∽△CBD，

∴

∴，故选：B．

2．如图，在中，是斜边上的高，则图中的相似三角形共有（   ）

A．1对 B．2对 C．3对 D．4对

【答案】C

【详解】∵∠ACB＝90°，CD⊥AB

∴△ABC∽△ACD，△ACD∽△CBD，△ABC∽△CBD

所以有三对相似三角形，

故选：C．

3．如图，在 Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，已知AD＝，那么BC＝_______．

【答案】

【详解】解：∵∠ACB＝90°，CD⊥AB，

∴∠ACB＝∠CDB＝90°，

∵∠B＝∠B，

∴△BCD∽△BAC，

∴＝，即＝，

∴,

∵

∴BC＝，

故答案为：．

4．如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，且＝．

（1）求证 △ACD∽△ABC；

（2）若AD＝3，BD＝2，求CD的长．

【答案】（1）见解析；（2）

【详解】（1）∵，，

∴；

（2）∵，

∴，，

∴，

∴，

∴，即，

∴．

5．中，，，点E为的中点，连接并延长交于点F，且有，过F点作于点H．

（1）求证：；

（2）求证：；

（3）若，求的长．

【答案】（1）证明见解析；（2）证明见解析；（3）4．

【详解】证明：（1），

，

，

，

在和中，，

；

（2）点为的中点，

，

由（1）已证：，

，

设，则，，

，

（等腰三角形的三线合一），

，

又，

，

即；

（3）由（2）已证：，

，

，

，

，即，

解得，

，

，

，

，

在和中，，

，

，

由（2）可知，设，则，

，

解得或（不符题意，舍去），

，

则在中，．