中考总复习数学（河南地区）题型一几何图形的折叠与动点问题课件

这是一份中考总复习数学（河南地区）题型一几何图形的折叠与动点问题课件，共60页。PPT课件主要包含了目录河南·中考，类型1，被动点落在特殊位置上，图形的相对位置不确定，高分技法，特殊图形的形状不定型，类型2，范围或最值型，类型3，含参问题等内容，欢迎下载使用。

类型1 动点或图形的相对位置不定型考点2 特殊图形的形状不定型考点3 含参、范围或最值型
动点或图形的相对位置不定型
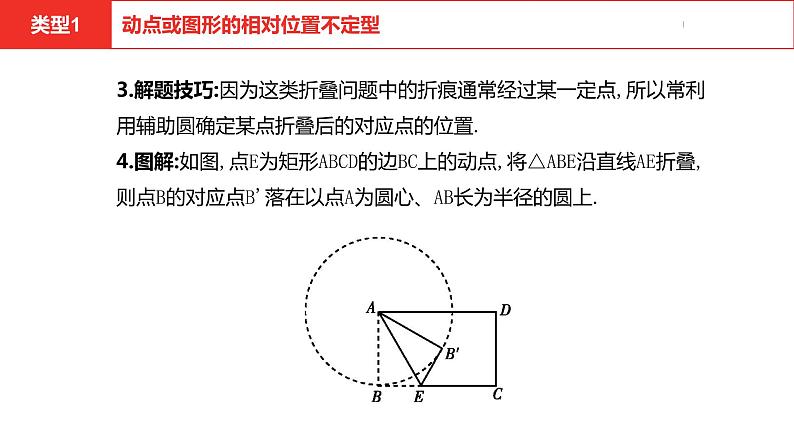
1.主动点、被动点的定义:如图,在矩形ABCD中,点E为边BC上的动点,将△ABE沿直线AE折叠,点B的对应点为B',其中点B'的位置随点E的位置的变化而变化,故定义点E为主动点,点B'为被动点.2.分类:1.
探究某点落在特殊位置问题
3.解题技巧:因为这类折叠问题中的折痕通常经过某一定点,所以常利用辅助圆确定某点折叠后的对应点的位置.4.图解:如图,点E为矩形ABCD的边BC上的动点,将△ABE沿直线AE折叠,则点B的对应点B'落在以点A为圆心、AB长为半径的圆上.
例1 如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上的一个动点,把△ADE沿AE折叠,当点D的对应点D'刚好落在矩形的对称轴上时,线段DE的长为_____. 【思路分析】　1.画图分析.(1)步骤1:根据条件确定被动点的位置.①点A是定点,点E是主动点,点D'为被动点,线段AD为定长,折叠后点D'到定点A的距离等于定长5,所以点D'的运动轨迹是圆的一部分;
②如图(1),以点A为圆心、AD长为半径作☉A;③作出矩形ABCD的两条对称轴,☉A与这两条对称轴的交点即为被动点D'(由图(1)可知有三种情况).
(2)步骤2:根据被动点的位置确定主动点的位置.根据折叠的性质可知,∠DAE=∠D'AE,所以点E在∠DAD'的平分线上,∠DAD'的平分线与射线DC的交点即为点E.2.分情况讨论.(1)情况1:点D'落在对称轴PQ上.①确定被动点D'的位置(根据条件定被动),如图(2);
②确定主动点E的位置(根据被动定主动),如图(3);
③确定解法.解法一(“一线三直角”模型法):如图(4),过点D'作CD的垂线,分别交CD,AB于点F,G,则FD'=D'G= ,DF=AG.在Rt△AGD'中,AD'=5,D'G= ,
解法二(“勾股定理”法):如图(4),过点D'作CD的垂线,分别交CD,AB于点F,G,则FD'=D'G= ,DF=AG.在Rt△AGD'中,AD'=5,D'G= ,
(2)情况2:点D'落在对称轴MN上,且在直线AB上方.①确定被动点D'的位置(根据条件定被动),如图(5);
②确定主动点E的位置(根据被动定主动),如图(6);
③确定解法.解法一(“一线三直角模型”法):如图(7),由折叠的性质得AD'=AD=5,∠AD'E=∠D=90°.由轴对称的性质,得AN=DM=4.在Rt△AND'中,由勾股定理得ND'= = =3,∴D'M=5-3=2.易证△AND'∽△D'ME,
(3)情况3:点D'落在对称轴MN上,且在直线AB下方.①确定被动点D'的位置(根据条件定被动),如图(8);
②确定主动点E的位置(根据被动定主动),如图(9);
③确定解法.解法一(“一线三直角”模型法):如图(10),过点D'作AD的垂线,交DA的延长线于点R,过点E作ES⊥RD'于点S,易知四边形DRSE是矩形,∴ES=DR,DE=RS.
在Rt△ARD'中,由勾股定理得AR= = =3,∴ES=DR=5+3=8.易证△ARD'∽△D'SE,∴ = ,即 ,∴D'S=6,∴DE=RS=4+6=10.
解法二(“勾股定理”法):如图(10),过点D'作AD的垂线,交DA的延长线于点R,过点E作ES⊥RD'于点S,易知四边形DRSE是矩形,∴ES=DR,DE=RS.在Rt△ARD'中,由勾股定理得AR 3,∴ES=DR=5+3=8.设D'E=DE=z,则D'S=ME=z-4.根据勾股定理可知ES2+D'S2=D'E2,即82+(z-4)2=z2,解得z=10.
例2 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC= ,点D是射线BC上一动点,作△ABD关于直线AD的对称图形,其中点B的对称点为E,连接BE,若∠CBE=15°,则线段BD的长为__________. 【思路分析】　1.画图分析.(1)步骤1:根据条件确定被动点的位置.①点A是定点,点D是主动点,点E为被动点,线段AB为定长,作轴对称变换后,点E到定点A的距离等于AB的长,所以点E的运动轨迹是圆的一部分;
②如图(1),以点A为圆心、AB长为半径作☉A;③作射线BP,使∠CBP=15°,则射线BP与☉A的交点(非点B)即为被动点E.(由图(1)可知有两种情况).
(2)步骤2:根据被动点的位置确定主动点的位置.根据轴对称的性质可知,∠DAE=∠DAB,所以点D在∠EAB的平分线上,∠EAB的平分线与射线BC的交点即为点D.2.分情况讨论.(1)情况1:射线BE在射线BC的下方.①确定被动点E的位置(根据条件定被动),如图(2);
②确定主动点D的位置(根据被动定主动),如图(3);
③确定解法.如图(4),在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC= ,∴AB=2,∠ABC=30°.由轴对称的性质可得,AE=AB,∠EAD=∠BAD,∴∠AEB=∠ABE=30°+15°=45°,∴∠BAE=90°,∴∠BAD= ∠BAE=45°.
(2)情况2:射线BE在射线BC的上方.①确定被动点E的位置(根据条件定被动),如图(5);
②确定主动点D的位置(根据被动定主动),如图(6);
③确定解法.如图(7),在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC= ,∴AB=2,∠ABC=30°.∵∠CBE=15°,∴∠ABE=15°=∠DBE.设AD,BE交于点H.∵点E,B关于直线AD对称,∴AD⊥BE.易证△ABH≌△DBH,∴BD=AB=2.
解决动点或图形的相对位置不定型问题的步骤1.确定被动点的位置:借助辅助圆确定被动点的位置及所有可能的情况;2.确定主动点的位置:在每种情况中,根据被动点的位置确定主动点的位置;3.确定解法:借助勾股定理、相似三角形或三角函数等,分情况进行求解.
这类问题是指特殊图形的边、角或对角线不确定,包括:(1)折叠后所得直角三角形中,不确定哪个内角是直角;(2)折叠后所得等腰三角形中,不确定哪条边是底边;(3)折叠后所得相似三角形中,不确定哪组角是对应角或哪组边是对应边;(4)折叠后所得四边形中,不确定所给的线段是边还是对角线.
(一)单动点的等腰三角形的形状不定型解题技巧:先利用“两圆一线”,确定等腰三角形的第三个顶点(即动点)的位置,再结合图形自身特点,寻求解题方法.图解:如图,在直线l上找一点C,使以点A,B,C为顶点的三角形是等腰三角形.方法:作“两圆一线”,“两圆”为分别以点A,B为圆心、AB的长为半径的圆,“一线”为线段AB的垂直平分线,它们与直线l的交点,即为要找的点C.
一、等腰三角形的形状不定型
例3 如图,在矩形ABCD中,AD=13,AB=24,点E是边AB上的一个动点,将△CBE沿直线CE折叠,得到△CB'E,连接AB',DB',若△ADB'为等腰三角形,则BE的长为_____________. 
【思路分析】　1.画图分析.(1)步骤1:根据条件确定被动点的位置.①点C是定点,点E是主动点,点B'为被动点,线段BC为定长,折叠后点B'到定点C的距离等于线段BC的长,所以点B'的运动轨迹是圆的一部分;②如图(1),以点C为圆心、BC长为半径作☉C;③作线段AD的垂直平分线,分别以点A,D为圆心、AD的长为半径作圆,这“两圆一线”与☉C在BC左侧的交点即为点B'.
(2)步骤2:根据被动点的位置确定主动点的位置.根据折叠的性质可知,∠B'CE=∠BCE,所以点E在∠BCB'的平分线上,∠BCB'的平分线与边AB的交点即为点E.2.分情况讨论.(1)情况1:DB'=AD,且点B'在CD下方.①确定被动点B'的位置(根据条件定被动),如图(2);
③确定解法.如图(4),过点B'作CD的垂线,分别交AB,CD于点N,M.易知☉D和☉C的半径相等,∴B'C=B'D,∴DM=CM=12.在Rt△B'CM中,B'M= = =5,∴B'N=13-5=8.∵∠CB'M+∠NB'E=90°,∠CB'M+∠B'CM=90°,∴∠NB'E=∠B'CM,∴cs∠NB'E=cs∠B'CM,∴ ,即 ,∴B'E= ,∴BE= .
(2)情况2:DB'=AD,且点B'在CD上方.①确定被动点B'的位置(根据条件定被动),如图(5);
③确定解法.如图(7),过点B'作CD的垂线,分别交AB,CD于点N,M.易知CM=12,B'C=13,∴在Rt△B'MC中,B'M= =5,∴B'N=5+13=18.∵∠EB'N+∠MB'C=90°,∠B'CM+∠MB'C=90°,∴∠B'CM=∠EB'N,∴cs∠B'CM=cs∠EB'N,∴ ,即 ,∴B'E= ,∴BE= .
(3)情况3:DB'=AB',且点B'在线段AD的垂直平分线上.①确定被动点B'的位置(根据条件定被动),如图(8);
③确定解法.如图(10),过点B'作CD的垂线,分别交AB,CD于点Q,P,则B'P=B'Q=,∴sin∠PCB' = ,∴∠PCB'=30°.∵∠QB'E+∠PB'C=90°,∠PCB'+∠PB'C=90°,∴∠QB'E=∠PCB'=30°,∴B'E= ,∴BE= .
(二)双动点的等腰三角形的形状不定型解题技巧:先大致确定图形形状,再利用等腰三角形“三线合一”的性质构造直角三角形,最后利用相似三角形、“同(等)角的同种三角函数值相同”或勾股定理进行求解.图解:如图(1),在矩形ABCD中,点P在对角线AC上从点A向点C运动,同时点Q在CB上从点C向点B运动,两点的运动速度相同,何时△CPQ是等腰三角形?
例4 如图,在矩形ABCD中,AB=2,AD=1,点E是AB上一动点,点F是AD上一动点(不与点D重合),连接EF,把△AEF沿直线EF折叠,使点A的对应点A'总落在DC边上,连接CE.若△A'EC是以A'E为腰的等腰三角形,则AF的长为_________.
【思路分析】　1.情况1:A'C=A'E.(1)画图分析.①确定被动点A'和主动点E的位置:在CD上取一点A',以点A'为圆心、A'C为半径作圆,交AB于点E,再以点E为圆心、A'E为半径作圆,当该圆经过点A时,点A'和点E的位置即可确定,如图(1);②确定主动点F的位置:根据∠AEF=∠A'EF,可知EF是∠AEA'的平分线,作∠AEA'的平分线,即可确定点F的位置. 图（1）
2.情况2:A'E=CE.(1)画图分析.①确定被动点A'和主动点E的位置:由EC=EA'=EA,可知点E在线段AC的垂直平分线上,作出线段AC的垂直平分线,即可确定点E的位置,再以点E为圆心、CE长为半径作圆,该圆与CD的交点(非点C)为点A',如图(3);②确定主动点F的位置:根据∠AEF=∠A'EF,可知EF是∠AEA'的平分线,作∠AEA'的平分线,即可确定点F的位置.
(2)确定解法.如图(4),连接AA',过点E作EH⊥CD于点H,则A'H=CH,EH=1.设A'F=AF=x,A'D=y,则DF=1-x,A'C=2-y,∴A'H=CH=1- ,∴AE=DH=y+1- =1+ .易证∠DAA'=∠FEA,∴tan∠DAA'=tan∠FEA,∴ ,即 ,∴x=y+ 　③.易证∠DFA'=∠HA'E,∴tan∠DFA'=tan∠HA'E,∴ ,即 ,∴x=1 　④.由③④可得 ,解得y= ,∴x= ,∴AF= .
二、直角三角形的形状不定型
(一)单动点的直角三角形的形状不定型解题技巧:先利用“两线一圆”,确定直角三角形第三个顶点(即动点)的位置,再结合图形自身特点,寻求解题方法.图解:如图,在直线l上找一点C,使△ABC为直角三角形.方法:作“两线一圆”,“两线”为分别过点A,B的AB的垂线,“一圆”为以AB为直径的圆,它们与直线l的交点,即为要找的点C.
例5 [2020开封一模]如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D,E分别为AC,BC的中点,点F为AB边上一动点,将∠A沿着直线DF折叠,点A的对应点为点G,且点G始终在直线DE的下方,连接GE,当△GDE为直角三角形时,线段AF的长为________.
【思路分析】　1.画图分析.(1)步骤1:根据条件确定被动点的位置.①点D是定点,点F是主动点,点G为被动点,线段AD为定长,折叠后点G到定点D的距离等于线段AD的长,所以点G的运动轨迹是圆的一部分;②如图(1),以点D为圆心、AD长为半径作☉D;③作线段DE的“两线一圆”,即分别过点D,E作DE的垂线,以DE为直径作圆,这“两线一圆”与☉D在直线DE下方的交点即为点G.(2)步骤2:根据被动点的位置确定主动点的位置.根据折叠的性质可知,∠ADF=∠GDF,所以点F在∠ADG的平分线上,∠ADG的平分线与边AB的交点即为点F.
2.分情况讨论.(1)情况1:∠GDE=90°,即DG⊥DE.①确定被动点G的位置(根据条件定被动),如图(2);
②确定主动点F的位置(根据被动定主动),如图(3);
③确定解法.在Rt△ABC中,∠A=30°,AB=8,∴AC=AB·cs∠BAC=8×cs 30°=4 ,∴AD=2 .如图(4),设DG与AB交于点H.∵点D,E分别为AC,BC的中点,∴DE∥AB,∴DG⊥AB.又∠DAH=30°,∴DH= ,∠ADH=60°,∴∠ADF=∠GDF=30°=∠DAF,∴AF=DF= 2.
(2)情况2:当∠DEG=90°,即DE⊥EG时,∵DE= AB=4,DG=AD=2 ,∴DE>DG,∴过点E的DE的垂线与☉D无交点,如图(5),故此情况不存在.(3)情况3:∠DGE=90°,即DG⊥EG.①确定被动点G的位置(根据条件定被动),如图(6);
②确定主动点F的位置(根据被动定主动),如图(7);
③确定解法.如图(8),∵DG=DC,DE=DE,∠DCE=∠DGE=90°,∴△DCE≌△DGE,∴∠GDE=∠CDE=30°,∴∠ADF=∠GDF=60°.又∠A=30°,∴∠AFD=90°,∴AF=AD·cs A=2 ×cs 30°=3.
(二)双动点的直角三角形的形状不定型解题技巧:先大致确定图形形状,再利用“相似”、“同(等)角的同种三角函数值相同”或勾股定理进行求解.图解:如图(1),在矩形ABCD中,点P在对角线AC上从点A向点C运动,同时点Q在CB上从点C向点B运动,两点的运动速度相同,何时△CPQ是直角三角形?
方法:如图(2),∠CQP=90°,由cs∠PCQ=cs∠ACB,得 ; 如图(3),∠CPQ=90°,由cs∠QCP=cs∠ACB,得 .
例6 [2020郑州适应性测试]如图,在矩形ABCD中,AB=3,BC=4,对角线AC,BD相交于点O,点E是AD边上一动点(不与点A,D重合),将△AEO沿直线EO折叠,点A落在点F处,线段EF,OD相交于点G.若△DEG是直角三角形,则线段DE的长为_________. 
(2)情况2:∠DEG=90°,即EF⊥AD.①确定点E,F,G的位置:在小圆O的右侧作一条竖直的与小圆O相切的直线,交AD于点E,交BD于点G,交 于点F,如图(4).
②确定解法.如图(5),易知HE=OH= ,∴DE=DH-HE= .
三、相似三角形的形状不定型
解题技巧:此类问题一般已知一组对应角,再分两种情况讨论.方法一:根据对应角相等分类求解;方法二:根据对应线段成比例分类求解.例7 [2018河南B卷]如图,在矩形ABCD中,点E为AB的中点,点F为射线AD上一动点,△A'EF与△AEF关于EF所在直线对称,连接AC,分别交EA',EF于点M,N,AB=2 ,AD=2.若△EMN与△AEF相似,则AF的长为______. 
【思路分析】　1.画图分析.(1)点E是定点,点F是主动点,点A',M,N均为被动点,线段AE为定长,易知A'E=AE,所以点A'的运动轨迹是以点E为圆心,AE的长为半径的圆的一部分,EF,EA'分别与AC交于点N,M.(2)以点E为圆心、AE的长为半径作☉E.(3)根据△EMN与△AEF相似,可知△EMN与△A'EF相似,则可分两种情况:①∠NME=90°,即EA'⊥AC(如图(1));②∠MNE=90°,即EF⊥AC(如图(2)).
2.分情况讨论.(1)情况1:∠NME=90°,即A'E⊥AC.①确定被动点A',M的位置,如图(3);
②确定主动点F、被动点N的位置,如图(4);
(2)情况2:∠MNE=90°,即EF⊥AC.①确定主动点F、被动点N的位置,如图(6);
②确定被动点A',M的位置,如图(7);
四、特殊四边形的形状不定型
解题技巧:此类问题一般已知一条线段为定线段,再分两种情况讨论.情况一:该线段为特殊四边形的边;情况二:该线段为特殊四边形的对角线.例8 如图,在Rt△ABC中, ∠BCA=90°, ∠BAC=30°,BC=1,点P为AB边上一动点(不与点A,B重合),点M为AC的中点,连接PC,PM,作△PCM关于直线PM的对称图形,点C的对应点为C',连接AC',当以点A,M,P,C'为顶点的四边形为平行四边形时,BP的长为______. 
【思路分析】　1.画图分析.(1)点M是定点,点P是主动点,点C'为被动点,线段MC为定长,由折叠的性质可知MC'=MC,所以点C'的运动轨迹是以点M为圆心、MC的长为半径的圆的一部分;(2)如图(1),以点M为圆心、MC的长为半径作☉M.(3)根据以点A,M,P,C'为顶点的四边形为平行四边形,可知分两种情况讨论:①AM为平行四边形的边;②AM为平行四边形的对角线.
2.分情况讨论.(1)情况1:定线段AM是平行四边形的边,即PC'∥MA.①确定主动点P的位置:∵PC' CM,∴四边形CMC'P是平行四边形.又MC=MC',∴四边形CMC'P是菱形,∴CP=CM.过点C作AB的垂线,点C到垂足之间的距离为 AC=CM,∴该垂足即为点P,如图(2).②确定被动点C'的位置:过点P作AC的平行线,该线与☉M的交点(位于点P右侧)即为点C',如图(3).
(2)情况2:定线段AM是平行四边形的对角线,即AP∥MC'.①确定被动点C'的位置:∵AP∥C'M,∴过点M作AB的平行线,该线与☉M在右下侧的交点即为点C',如图(5).
②确定主动点P的位置:连接AC',过点M作AC'的平行线,该线与AB的交点即为点P,如图(6).
解题技巧:解决含参问题,关键是根据题意画出各种情况的图形,再利用相似三角形、三角函数或勾股定理列出关于参数的方程进行求解.例9 如图,在边长为a的正方形ABCD中,点E为射线DA上一动点(不与点A重合),连接CE,以直线CE为对称轴作点D的对称点D',连接D'E,D'C,D'A,D'B.当△ABD'是以AD'为底边的等腰三角形时,AE=2,则a的值为_______. 
【思路分析】　1.画图分析.(1)点C是定点,点E是主动点,点D'是被动点,线段CD为定长,由轴对称变换可知D'C=DC,所以点D'的运动轨迹是以点C为圆心、CD的长为半径的圆的一部分.(2)如图(1),以点C为圆心、CD的长为半径作☉C.由AD'是等腰三角形的底,可知AB=BD',故以点B为圆心、AB的长为半径作圆,该圆与☉C的交点即为点D'. 
2.分情况讨论.(1)情况1:BA=BD',且点D'在BC的左侧.①确定被动点D'的位置(根据条件定被动),如图(2). 
②确定主动点E的位置(根据被动定主动):作∠DCD'的平分线,该线与AD的交点即为点E,如图(3). 
(2)情况2:BA=BD',且点D'在BC的右侧.①确定被动点D'的位置(根据条件定被动),如图(5). 
②确定主动点E的位置(根据被动定主动):作∠DCD'的平分线,该线与射线DA的交点即为点E,如图(6). 
解法二:如图(7),∵BD'=AB=BC=CD=CD',∴△D'BC是等边三角形,∴∠D'CB=60°,∴∠DCD'=150°,∴∠DCE=∠D'CE=75°.根据tan 75°=2+ ,tan∠DCE= ,可得 ,解得a= -1. 
说明:熟记15°或75°角的正切值及其推导方法有助于快速解决问题.①在Rt△ABC中,∠ABC=30°,AC=1,在CB的延长线上截取一点D,使BD=AB,连接AD,如图(1).
②在Rt△ADC中,∠ADC=15°,AC=1,作AD的垂直平分线,交CD于点B,连接AB,如图(2).
(一)单动点范围问题解题技巧:此类问题一般先根据被动点的运动特征,作出辅助圆,利用辅助圆分析符合题意的运动过程,再分析临界情况,进而得到相关线段或角度的取值范围.例10 [2020许昌二模]如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,点D是边AC上一动点(不与点A,C重合).连接BD,将△ABD沿直线BD折叠,点A落在A'处,当点A'在△ABC的内部(不含边界)时,AD长度的取值范围是_______.　　　
【思路分析】　1.画图分析.(1)点B是定点,点D是主动点,点A'是被动点,线段AB为定长,由折叠的性质可知A'B=AB,所以点A'的运动轨迹是以点B为圆心、AB的长为半径的圆的一部分.(2)如图(1),以点B为圆心、AB的长为半径作☉B,分别交AC,BC于点M,N.由点A'在△ABC的内部(不含边界)运动,故当点A'在 上(不含点M,N)运动时符合题意.　　
2.分临界情况讨论.(1)临界情况1:当点A'是☉B与AC的交点时,作∠ABA'的平分线,该线与AC的交点即为点D,如图(2).　　
如图(3),∵BA=BA',BD平分∠ABA',∴BD⊥AC.(2)临界情况2:当点A'是☉B与BC的交点时,作∠ABA'的平分线,该线与AC的交点即为点D,如图(4).
如图(5),易知∠ABD=∠A'BD= ∠ABC=45°.过点D作DE⊥AB于点E,则DE=BE.
(二)双动点范围问题解题技巧:连接定点和其对应点,作所连线段的垂直平分线,则该线即为动直线,可根据对应点在某条线上的运动情况,确定所求线段的取值范围.图解:如图(1),点E,F分别为矩形ABCD的边AB,BC上的动点,将△BEF沿直线EF折叠,使点B的对应点B'落在边AD上,如何确定BE的取值范围?
方法:将点B'看作AD上的动点,连接BB',作线段BB'的垂直平分线,该线与AB,BC的交点分别为点E,F.如图(2),移动点B'使直线EF经过点A,此时BE有最大值;如图(3),移动点B'使直线EF经过点C,此时BE有最小值.
例11 如图,在平行四边形ABCD中, AB=2,BC=2 ,∠B=45°,点E,F分别是边AB,BC上的动点(含端点),将△BEF沿EF所在直线折叠,使点B落在直线AD上的点B'处,则 DB'的长的取值范围是________. 
【思路分析】　1.画图分析.(1)如图(1),连接BB',作线段BB'的垂直平分线,该线与AB的交点为E,与BC的交点为F,此时点B'相当于主动点,点E,F相当于被动点.(2)移动主动点B',随着点B'的运动,找到直线EF的临界位置,即当直线EF经过点A时(如图(2))和当直线EF经过点C时(如图(3)).
(一)两点之间线段最短例12 如图,在矩形ABCD中,AB=4,AD=2,点M是AD边的中点,点N是AB边上的一动点,作△AMN关于直线MN的对称图形,点A的对应点为A',连接A'C.在MN上有一动点P,连接A'P,CP,则△A'PC周长的最小值是_________ . 
【思路分析】　1.画图分析.由轴对称变换可知MA=MA',点A'在以点M为圆心、MA的长为半径的圆上运动,点N为主动点,点A',P为被动点,分三步确定动点位置:①先判断点P的大致位置:由AP=A'P,可知当A,P,C三点共线时,AP+PC有最小值,即A'P+PC有最小值,最小值为AC的长,如图(1);
②再定点A'的位置:由点A'在以点M为圆心、MA的长为半径的圆上运动,可知当M,A',C三点共线时,A'C有最小值,最小值为MC-MA,如图(2);③最后定主动点N的位置及被动点P的具体位置:作AA'的垂直平分线或∠AMA'的平分线,与AB的交点即为点N,MN与AC的交点为点P,如图(3).
“两点之间线段最短”最值问题的常见类型1.两定一动(1)如图(1),在直线l两侧各有一个定点A,B,在直线l上求作点P,使得PA+PB的值最小.构图:连接AB,AB与直线l的交点即为点P,如图(2)所示.
(2)如图(3),在直线l同侧有两个定点A,B,在直线l上求作点P,使得PA+PB的值最小.构图:作点A关于直线l的对称点A',连接A'B,A'B与直线l的交点即为点P,如图(4)所示.
(3)如图(5),在直线l同侧有两个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大.　　　　构图:连接BA并延长,BA的延长线与直线l的交点即为点P,如图(6)所示.
(4)如图(7),在直线l两侧各有一个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大.　构图:作点B关于直线l的对称点B',连接AB'并延长,AB'的延长线与直线l的交点即为点P,如图(8)所示.
(5)延伸:如图(9),在直线l同侧有两个定点A,B,在直线l上求作点P,使得|PA-PB|的值最小.　　　构图:连接AB,作线段AB的垂直平分线,该线与直线l的交点即为点P,此时|PA-PB|=0,如图(10)所示.
2.一定两动(1)如图(11),点P在∠AOB的内部,在OA上求作一点C,在OB上求作一点D,使△PCD的周长最小.构图:分别作点P关于OA,OB的对称点P',P″,连接P'P″,分别交OA,OB于点C,D,此时△PCD的周长最小,最小值即为P'P″的长,如图(12)所示.
(2)如图(13),点P在∠AOB的内部,在OA上求作一点C,在OB上求作一点D,使PD+CD的值最小.　　　　　构图:作点P关于OB的对称点P',过点P'作P'C⊥OA,交OB于点D,交OA于点C,此时PD+CD的值最小,最小值即为P'C的长,如图(14).
3.两定两动如图(15),点P,Q在∠AOB的内部,在OA,OB上分别求作点C,D,使得四边形PCDQ的周长最小.　　　　 构图:作点P关于OA的对称点P',作点Q关于OB的对称点Q',连接P'Q',分别交OA,OB于点C,D,此时四边形PCDQ的周长最小,最小值为PQ+P'Q',如图(16)所示.
4.两定点两定直线:在直线m,n上分别求作点P,Q,使得PA+PQ+QB的值最小.(1)如图(17),A,B两点在两直线的外侧.构图:连接AB,分别交直线m,n于点P,Q,此时PA+PQ+QB的值最小,如图(18).
(2)如图(19),点B在两直线内侧,点A在两直线外侧.　　构图:作点B关于直线n的对称点B',连接AB',分别交直线m,n于点P,Q,此时PA+PQ+QB的值最小,最小值为AB'的长,如图(20).
(3)如图(21),A,B两点都在两直线内侧.构图:作点A关于直线m的对称点A',作点B关于直线n的对称点B',连接A'B',分别交直线m,n于点P,Q,此时PA+PQ+QB的值最小,最小值为A'B'的长,如图(22).
(二)垂线段最短例13 [2019平顶山三模]如图,在菱形ABCD中,AB=2,∠BAD=120°,点E,F分别是边AB,BC上的动点,将△BEF沿直线EF折叠,使点B的对应点B'始终落在边CD上,则A,E两点之间的最大距离为__________. 
【思路分析】　由折叠的性质,可知EB=EB',当BE的值最小,即B'E的值最小时,AE的值最大.∵点E是边AB上的动点,点B'是边DC上的动点,根据“垂线段最短”可确定当B'E⊥DC时,B'E最小,最终将问题转化为求点A到DC的距离即可.如图,过点A作AH⊥CD于点H,在Rt△ADH中,∠D=60°,AD=2,∴AH=ADsin D=2×sin 60°= ,故B'E的最小值为 ,故AE的最大值为2- .
(三)利用函数性质求最值解题技巧:选择合适的变量,设出未知数,并用含该未知数的代数式表示所要求的线段长、周长或面积等,最后利用二次函数的性质进行求解.例14 [2020湖北武汉中考改编]如图,折叠矩形纸片ABCD,使点D落在AB边上的点M处(不与点A重合),EF为折痕,若AB=1,AD=2,则四边形CDEF面积的最小值是__.