


中考总复习数学(河南地区)第五章四边形课件
展开考点1 平行四边形考点2 多边形考点3 正多边形
命题角度1 与平行四边形性质有关的计算命题角度2 平行四边形的判定
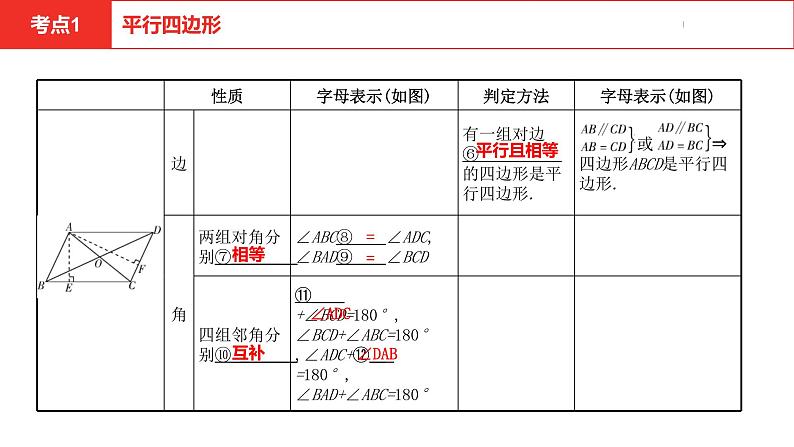
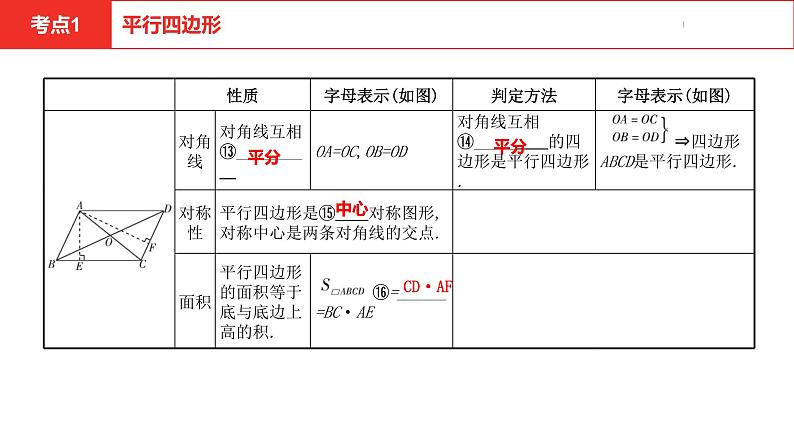
1.定义:两组对边分别平行的四边形叫做平行四边形.2.性质与判定
每条边都相等的多边形不一定是正多边形,因为它的内角不一定都相等,如菱形;每个内角都相等的多边形也不一定是正多边形,因为它的边不一定相等,如矩形.
与平行四边形性质有关的计算
例1(逻辑推理)[2020平顶山三模]如图,在▱ABCD中,BE垂直平分CD于点E,且∠BAD=45°,AD=3,则▱ABCD的对角线AC的长为 ( )
利用平行四边形的性质进行相关计算的方法1.求角度:先将题中的已知角找出来,再结合平行四边形的性质(即对角相等,邻 角互补及对边平行),将所求角与已知角逐渐联系起来.2.求线段长:(1)根据平行四边形的性质将已知条件转化到一个三角形中,利用勾股定理、直角三角形的性质、等腰三角形的性质、三角函数或三角形面积公式等进行求解;(2)根据平行四边形的性质,利用中位线定理、平行线分线段成比例定理、全等三角形的判定与性质或相似三角形的判定与性质,求线段长或线段比值.
例2 如图,在四边形ABCD中,AD∥BC,AD=5 cm,BC=9 cm.点M是CD的中点,点P是BC边上的一动点(不与点B,C重合),连接PM并延长交AD的延长线于点Q.(1)连接CQ,PD,试说明不管点P在何位置,四边形PCQD始终是平行四边形.(2)当PC的长度为多少时,四边形ABPQ是平行四边形?【思路分析】 (1)
(1)∵AD∥BC,∴∠QDM=∠PCM,∠DQM=∠CPM.∵点M是CD的中点,∴DM=CM,∴△PCM≌△QDM,∴DQ=PC.又DQ∥PC,∴四边形PCQD是平行四边形,∴不管点P在何位置,四边形PCQD始终是平行四边形.
(2)当四边形ABPQ是平行四边形时,PB=AQ,∴BC-CP=AD+QD,∴9-CP=5+CP,∴CP=2.∴当PC=2 cm时,四边形ABPQ是平行四边形.
解决与平行四边形的判定相关的问题的方法1.平行四边形的判定问题往往以判定线段相等、角相等、直线平行或线段互相平分等形式出现.证明一个四边形是平行四边形,往往有多种证明思路,因此必须仔细分析,通过比较,选择最简捷的证明思路,方法如下:(1)已知一组对边相等(2)已知一组对边平行(3)若图中有对角线——证对角线互相平分.
解决与平行四边形的判定相关的问题的方法2.涉及动点问题,常见的命题模式是“当某线段取何值时,以某四个点为顶点的四边形为平行四边形”,解题时要注意运用逆向思维,即将要判定的平行四边形作为已知条件,利用其性质去求线段的长,且要注意正向检验.
与平行四边形有关的折叠问题
例3 如图,在▱ABCD中,∠B=45°,AB=4,BC=8,点E为AB的中点,点F是BC上一动点,连接EF,将△BEF沿EF翻折,得到△GEF,当EG与▱ABCD的一边垂直时,BF的长度为_____________________________.
【思路分析】 第一步,确定点G的位置:∵点E为定点,EG=EB,即EG的长度固定,∴点G在以点E为圆心、EB的长为半径的圆上.如图,过点E分别作AB,BC的垂线,两线与☉E的交点即为符合题意的点G(其中点G在G4的位置上时,点F不在线段BC上,故此种情况不存在).第二步,分情况讨论:根据点G的位置,分情况画出图形,再根据条件进行求解.
解决与平行四边形有关的折叠问题的一般方法1.根据动点运动情况,结合隐形圆和题意,找到符合题意的动点的位置;2.分情况画出图形,再根据轴对称和平行四边形的性质,把条件或结论转移到三角形中,利用方程、三角函数、勾股定理或相似三角形的性质进行求解.
第二节 矩形、菱形和正方形
考点1 矩形、菱形和正方形的性质考点2 矩形、菱形和正方形的判定考点3 中点四边形
课时一 矩形的判定与性质命题角度1 与矩形性质有关的计算命题角度2 矩形的判定命题角度3 与矩形相关的折叠问题
课时二 菱形的判定与性质命题角度4 与菱形的性质有关的计算命题角度5 菱形的判定命题角度6 与菱形相关的折叠问题
课时三 正方形的判定与性质命题角度7 与正方形性质有关的计算命题角度8 正方形的判定命题角度9 与正方形相关的折叠问题
矩形、菱形和正方形的性质
矩形、菱形和正方形的判定
1.定义:依次连接任意一个四边形各边的中点所得的四边形叫做中点四边形.2.常见结论
例1 (逻辑推理)[2020开封二模]如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴、y轴上,且OA=5,OC=3.把矩形OABC绕着点O逆时针旋转,使点A的对应点A1恰好落在BC边上,则点C的对应点C1的坐标为 ( )
例2 如图,∠MON=90°,矩形ABCD在∠MON的内部,顶点A,B分别在射线OM,ON上,AB=4,BC=2,则点D到点O的最大距离是_________.
【思路分析】 设AB的中点为E,连接OE,DE,可知OE,DE的长度均一定,当O,E,D三点共线时,OD的长度最大,据此求解即可.
例3 如图,在矩形ABCD中,AB=3 cm,BC=4 cm,点E,F均位于对角线AC上,且AE=CF=1 cm.点G从点D出发,以1 cm/s的速度向点A运动,同时点H从点B出发,以相同的速度向点C运动,运动时间为t s,且0≤t<4.(1)求证:△AFG≌△CEH;(2)当t=__________时,四边形EHFG为矩形.
【思路分析】 (1)要证明三角形全等,需根据条件找到相等的对应边、相等的对应角,再根据全等三角形的判定定理进行证明.找相等的对应角:由AD∥BC,得∠GAF=∠HCE.找相等的对应边:由AE=CF,得AF=CE;由点G,H的速度相同,得DG=BH,从而得AG=CH.最后利用SAS证明即可.(2)将四边形EHFG为矩形作为条件,连接HG,得到HG与EF相等且互相平分,再结合题中条件进行求解.
(1)证明:∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∴∠GAF=∠HCE.∵DG=BH=t,∴AG=CH=4-t.∵AE=CF,∴AF=CE,∴△AFG≌△CEH.(2)2解法提示:如图,当四边形EHFG为矩形时,连接GH,交AC于点O,则GH=EF=5-2=3,OE=OF= ,∴GH=AB,OA=OC= ,∴GH∥AB,且点G为AD的中点,∴t 2.
动点问题中矩形的动态探究题的考查方式和解题方法1.考查方式: 通过探究动点的运动时间来判定四边形的形状.2.解题方法:以题目所要求的矩形为条件,先将图形特殊化,或画出满足题意的图形,结合矩形的性质(如对边平行且相等、内角均为90°、对角线相等等),进行逆推,得到相应的条件.
例4 (逻辑推理、数学运算)如图,在矩形ABCD中,BC=12,AB= ,点E为AD的中点,点F为射线AB上一点,连接CF,BF=2,若将△AEF沿直线EF折叠后,点A恰好落到CF上的点G处,则 的值为______________________.
解决矩形折叠问题的步骤1.一折:看怎么折,折痕在哪儿;2.二等:位于折痕两侧的图形关于折痕成轴对称,即折叠前后的两部分全等,对应边、对应角、对应线段、周长、面积等均相等,且折叠后,对应点(不重合时)的连线被折痕垂直平分;3.三设:选择合适的线段或角,并设其为x;
解决矩形折叠问题的步骤4.四列:根据勾股定理、三角函数、全等三角形的性质或相似三角形的性质列方程;5.五解:解上述方程;6.六验:根据题中条件,验证解得的x值是否符合题意.
与菱形的性质有关的计算
例5 (逻辑推理、数学运算)[2019四川绵阳]如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线的交点E的坐标为 ( )
利用菱形的性质进行相关计算的三种题型1.求角度.应注意菱形的四条边相等、对角相等和邻角互补等,可利用等腰三角形的性质和平行线的相关性质转化要求的角,直到找到与已知角的关系;
利用菱形的性质进行相关计算的三种题型2.求长度(线段或周长).应注意使用等腰三角形的性质,若菱形中有一个顶角为60°,则连接另外两点的对角线所形成的两个三角形均为等边三角形,在计算时可借助等边三角形的性质;若菱形中存在直角三角形,则应注意使用勾股定理、直角三角形斜边上的中线等于斜边的一半等进行求解;3.求面积.可直接利用S=底×高来求解,也可利用面积等于对角线之积的一半来进行求解.
例6 [2020安阳二模改编]如图,在锐角三角形ABC中,AB=AC=4,以AB为直径的☉O分别交BC,AC于点F,G,点E是边AC的中点,过点A作AD∥BC,交BE的延长线于点D,连接CD.(1)求证:四边形ABCD是平行四边形.(2)当 的长度为_____时,四边形ABCD是菱形.
(1)证明:∵AD∥BC,∴∠DAE=∠BCE.∵点E是AC中点,∴AE=CE.在△ADE和△CBE中,∴△ADE≌△CBE.∴AD=CB.又∵AD∥BC,∴四边形ABCD是平行四边形.
(2) 解法提示:当四边形ABCD是菱形时,AB=BC.又∵AB=AC,∴△ABC是等边三角形,∴∠BAC=∠ABC=60°.连接OF,OG,∴OB=OF=OG=OA,∴△OBF,△OAG是等边三角形,∴∠BOF=∠AOG=60°,∴∠FOG=180°-60°-60°=60°,
动点问题中菱形的动态探究题的考查方式和解题方法1.考查方式: 通过探究动点的运动情况来判定四边形的形状.2.解题方法:以题目所要求的菱形为条件,先将图形特殊化,或画出满足题意的图形,结合菱形的性质(如四边相等、对角线垂直等),进行逆推,得到相应的条件.注意:解决以圆为背景的菱形存在性问题时,常结合圆的半径,将菱形问题转化为等边三角形问题进行解决.
例7 如图,在菱形ABCD中,∠ABC=60°,AB=4,点E为AB的中点,点F为线段BC上一动点,连接EF,将△BEF沿直线EF翻折,得到△GEF,当EG与菱形ABCD的对角线垂直时,BF的长为___________.
与正方形性质有关的计算
例8 [2020山东青岛]如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G,连接DF.若DE=2,OF=3,则点A到DF的距离为_____. 【思路分析】 根据条件求DF的长及△ADF的面积,即可得解.
例9 (逻辑推理、直观想象)如图,在Rt△ABC中,∠ACB=90°,过点C作直线MN∥AB,点D为AB的中点,过点D作DE⊥BC,交直线MN于点E,垂足为点F,连接CD,BE.(1)求证:CE=AD.(2)当△ABC满足什么条件时,四边形CDBE是正方形?请说明你的理由.
【思路分析】 (1)先证AC∥DE,再证四边形ADEC是平行四边形,问题得证.(2)根据四边形CDBE是正方形,可得CD⊥BD,结合点D为AB的中点,可知直线CD是AB的垂直平分线,可得CA=CB,问题得解.【自主解答】
(1)证明:∵DE⊥BC,∠ACB=90°,∴AC∥DE.又MN∥AB,∴四边形ADEC是平行四边形,∴CE=AD.(2)当△ABC是等腰直角三角形时,四边形CDBE是正方形.理由:由四边形CDBE是正方形,可得CD⊥BD.又点D为AB的中点,∴直线CD是AB的垂直平分线,∴CA=CB.又∠ACB=90°,∴△ABC是等腰直角三角形.
动点问题中正方形的动态探究题的考查方式和解题方法1.考查方式: 通过探究动点的运动情况来判定四边形的形状.2.解题方法:以题目所要求的正方形为条件,先将图形特殊化,或画出满足题意的图形,结合正方形的性质(如四边相等、对角线互相垂直平分、对角线平分一组对角等),进行逆推,得到相应的条件.
与正方形有关的折叠问题
例10 如图,正方形ABCD中,AB=4,E是AB的中点,F是AD上的动点,连接EF,将△AEF沿直线EF翻折得到△A'EF,连接A'B,A'C,则当AF=___ 时,△A'BC是等腰三角形.
【思路分析】 第一步,确定点A'的位置:∵点E为定点,EA'=EA,即EA'的长度固定,∴点A'在以点E为圆心、EA为半径的圆上.如图,分别以点B,C为圆心、BC的长为半径作圆,作线段BC的垂直平分线,这“两圆一线”与☉E的交点即为符合题意的点A'.第二步,分情况讨论:根据点A'的位置,分情况画出图形,再根据条件进行求解.
特殊四边形与圆的综合题规范性解答
中考总复习数学(河南地区)题型三二次函数综合题课件: 这是一份中考总复习数学(河南地区)题型三二次函数综合题课件,共60页。PPT课件主要包含了目录河南·中考,线段问题,类型1,方法总结,高分技法,典例变式1,自主解答,典例变式2,典例变式3,典例变式4等内容,欢迎下载使用。
中考总复习数学(河南地区)第一章数与式课件: 这是一份中考总复习数学(河南地区)第一章数与式课件,共54页。PPT课件主要包含了实数的分类,考点1,按定义分,名师点拨,考点3,温馨提示,归纳总结,实数的运算,考点4,四则运算法则等内容,欢迎下载使用。
中考总复习数学(河南地区)第三章函 数课件: 这是一份中考总复习数学(河南地区)第三章函 数课件,共60页。PPT课件主要包含了考点1,对称点的坐标特征,考点2,自变量的取值范围,考点3,解析式法,命题角度1,点的坐标的规律探索,命题角度2,提分技法等内容,欢迎下载使用。












