江苏十三市2022学年九年级上学期数学期末真题压轴精选——解答题30道

江苏地区2022学年九年级上学期数学期末真题压轴精选

【解答题30道】

1．（2022·江苏·宿迁期末）如图，点P在⊙O外，M为OP的中点，以点M为圆心，以MO为半径画弧，交⊙O于点A，B，连接PA；

（1）判断PA与⊙O的位置关系，并说明理由；

（2）连接AB，若OP＝9，⊙O的半径为3，求AB的长．

2．（2022·江苏扬州期末）如图，抛物线与轴交于、两点，与轴交于点．直线与抛物线交于、两点，与轴交于点，点的横坐标为4．

(1)求抛物线的解析式与直线的解析式；

(2)若点是抛物线上的点且在直线上方，连接、，求当面积最大时点的坐标及该面积的最大值；

(3)若点是抛物线上的点，且，请直接写出点的坐标．

3．（2022·江苏镇江期末）已知抛物线y＝﹣x2＋bx＋c与x轴交于A、B两点（点A在点B的左侧），与y轴的交点为C(0，3)，其对称轴是直线x＝1，点P是抛物线上第一象限内的点，过点P作PQ⊥x轴，垂足为Q，交BC于点D，且点P的横坐标为m．

(1)求这条抛物线对应的函数表达式；

(2)如图1，PE⊥BC，垂足为E，当DE＝BD时，求m的值；

(3)如图2，连接AP，交BC于点H，则的最大值是      ．

4．（2022·江苏·射阳县期末）如图，在平面直角坐标系xOy中，抛物线与两坐标轴分别相交于A，B，C三点

(1)求A，B，C三点坐标．

(2)求证：∠ACB=90°

(3)点D是第一象限内该抛物线上的动点，过点D作x轴的垂线交BC于点E，交x轴于点F．求DE+BF的最大值．

5．（2022·江苏南通期末）定义：，，是二次函数图象上任意三个不重合的点，若满足，，中任意两数之和大于第三个数，任意两数之差小于第三个数，且，，都大于0，则称函数是上的“仿三角形函数”．

(1)①函数的最小值是，最大值是，则______（填写“>”，“<”或“=”）；

②函数______上的“仿三角形函数”；（填写“是”或者“不是”）

(2)若二次函数是上的“仿三角形函数”，求的取值范围；

(3)若函数在上是“仿三角形函数”，求的取值范围．

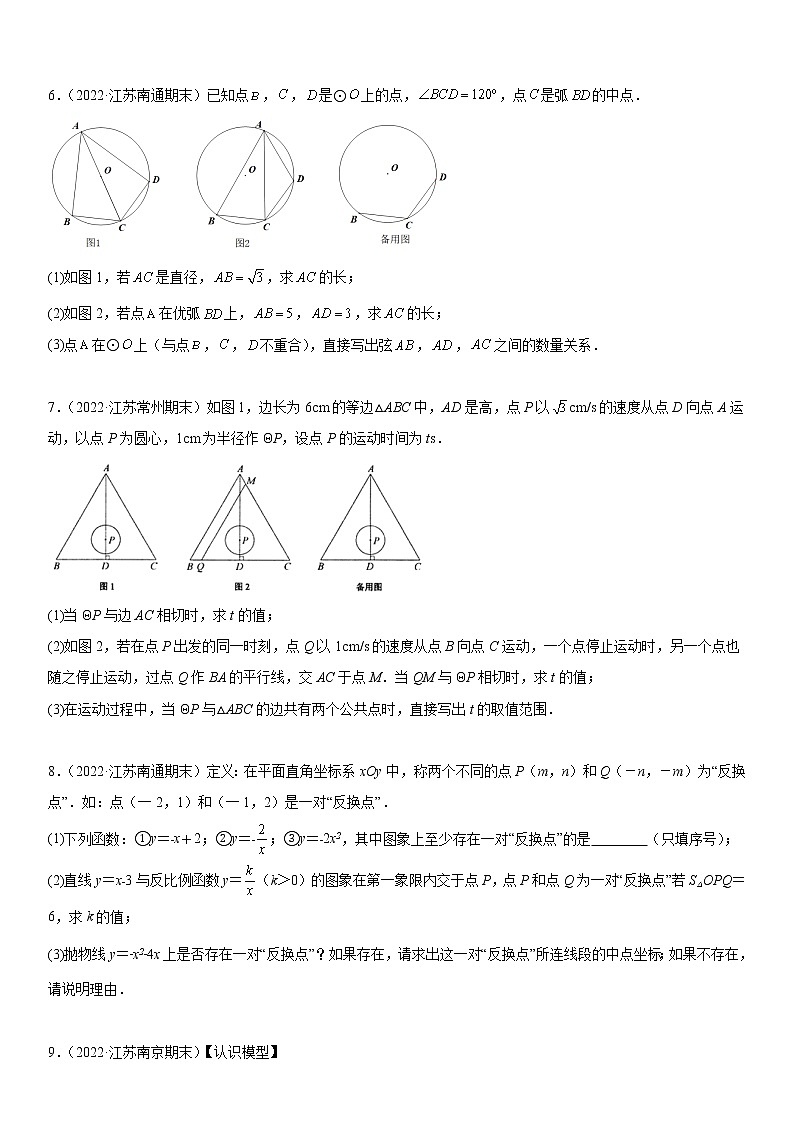
6．（2022·江苏南通期末）已知点，，是⊙上的点，，点是弧的中点．

(1)如图1，若是直径，，求的长；

(2)如图2，若点在优弧上，，，求的长；

(3)点在⊙上（与点，，不重合），直接写出弦，，之间的数量关系．

7．（2022·江苏常州期末）如图1，边长为6cm的等边△ABC中，AD是高，点P以cm/s的速度从点D向点A运动，以点P为圆心，1cm为半径作ΘP，设点P的运动时间为ts．

(1)当ΘP与边AC相切时，求t的值；

(2)如图2，若在点P出发的同一时刻，点Q以1cm/s的速度从点B向点C运动，一个点停止运动时，另一个点也随之停止运动，过点Q作BA的平行线，交AC于点M．当QM与ΘP相切时，求t的值；

(3)在运动过程中，当ΘP与△ABC的边共有两个公共点时，直接写出t的取值范围．

8．（2022·江苏南通期末）定义：在平面直角坐标系xOy中，称两个不同的点P（m，n）和Q（－n，－m）为“反换点”．如：点（一2，1）和（一1，2）是一对“反换点”．

(1)下列函数：①y＝﹣x＋2；②y＝﹣；③y＝﹣2x2，其中图象上至少存在一对“反换点”的是 　   　（只填序号）；

(2)直线y＝x﹣3与反比例函数y＝（k＞0）的图象在第一象限内交于点P，点P和点Q为一对“反换点”若S△OPQ＝6，求k的值；

(3)抛物线y＝﹣x2﹣4x上是否存在一对“反换点”？如果存在，请求出这一对“反换点”所连线段的中点坐标；如果不存在，请说明理由．

9．（2022·江苏南京期末）【认识模型】

(1)如图1，直线l1∥l2，直线m、n分别与l1、l2交于点A、B和点F、D，m和n交于点E．则＝       ；　　　

【应用模型】

(2)如图2，在△ABC中，D是边AB上一点，且．若BC＝4，AB＝10，求AC的长．

10．（2022·江苏南京期末）问题呈现：探究二次函数（其中，m为常数）的图像与一次函数的图像公共点．

(1)问题可转化为：二次函数的图像与一次函数______的图像的公共点．

(2)问题解决：在如图平面直角坐标系中画出的图像．

(3)请结合（2）中图像，就m的取值范围讨论两个图像公共点的个数．

(4)问题拓展：若二次函数（其中，m为常数）的图像与一次函数的图像有两个公共点，则m的取值范围为______．

11．（2022·江苏·盐城期末）问题背景：如图1，在矩形ABCD中，AB=2，∠ABD=30°，点E是边AB的中点，过点E作EF⊥AB交BD于点F．

(1)在一次数学活动中，小王同学将图1中的△BEF绕点B按逆时针方向旋转90°，如图2所示，得到结论：①=______ ；②直线AE与DF所夹锐角的度数为 _______．

(2)小王同学继续将△BEF绕点B按逆时针方向旋转，旋转至如图3所示位置．请问探究（1）中的结论是否仍然成立？并说明理由．

(3)根据以上探究，将△BEF绕点B按顺时针方向旋转180°，设直线AE与DF的交点为P，在旋转过程中，点P的位置也随之改变，请思考点P运动的轨迹，直接写出点P运动的路程_______．（结果保留π）

12．（2022·江苏·盐城期末）已知抛物线y＝﹣x2+bx+c与x轴交于A、B两点（点A在点B的左侧），与y轴的交点为C（0，3），其对称轴是直线x＝1，点P是抛物线上第一象限内的点，过点P作PQ⊥x轴，垂足为Q，交BC于点D，且点P的横坐标为a．

(1)求这条抛物线对应的函数表达式；

(2)如图1，过点C作CE平行于x轴，交抛物线于点E，若点P在CE的上方，连接PE，PC，DE，当S四边形CPED=S△AOC时，求点P坐标；

(3)如图2，连接AP，BP，设AP交BC于点H，△PHB的面积为S1，△ABH的面积为S2 ，求的最大值；

(4)如图3，在（3）的条件下，连接CQ，将CQ右侧的抛物线沿CQ翻折，交y轴于点M，请直接写出点M的坐标．

13．（2022·江苏镇江期末）如图：已知线段，射线AS垂直于AM，点N在射线AS上，设，点P在经过点N且平行于AM的直线上运动，的平分线交直线NP于点Q，过点Q作，交线段AM于点B，连接PB交AQ于点C，以Q为圆心，QC为半径作圆．

(1)求证：PB与相切；

(2)已知的半径为3，当AM所求直线与相切时，求n的值及PA的长；

(3)当时，若与线段AM只有一个公共点，则的半径的取值范围是______．

14．（2022·江苏徐州期末）如图，抛物线与x轴交于两点A（1，0）、B（4，0），与y轴交于点C（0，﹣3），P为抛物线上的动点，直线l经过B、C两点．

(1)求抛物线的表达式；

(2)点P在第一象限，以P为圆心的圆与BC相切，随着点P的运动，⊙P的面积是否存在最大值？若存在，求出最大值（结果保留π）；若不存在，说明理由．

15．（2022·江苏泰州期末）如图（1），已知点P是抛物线的顶点，矩形ABCD中，顶点A、B在该抛物线上（其中点A在第一象限），顶点C、D在x轴上，连接线段BD、PD、BP，DP、AB交于点E．

(1)若D点坐标为（m，0），则点A、B、P坐标分别为A        、B        、P        （可用含m的代数式表示）．

(2)如图（1），①求证：；②连接PA．求证：

(3)解决完以上问题后，小明不禁自问：是不是只有抛物线才有（2）中的结论呢？善于思考的小明将作一般化处理，为研究方便，不妨设，请解决小明提出的如下两个问题：

①如图（1）抛物线中字母a、c满足什么条件才能使．并说明理由；

②如图（2）抛物线中字母a、b、c满足什么条件才能使．请直接写出结论．

16．（2022·江苏连云港期末）如图，直线y=﹣x+3与x轴交于点C，与y轴交于点B，抛物线y=ax2+x+c经过B、C两点．

（1）求抛物线的解析式；

（2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC面积的最大值；

（3）在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．

17．（2022·江苏南京期末）（1）如图1，将直角三角板的直角顶点放在正方形ABCD上，使直角顶点与D重合，三角板的一边交AB于点P，另一边交BC的延长线于点Q．则DP        DQ（填“＞”“＜”或“＝”）；

（2）将（1）中“正方形ABCD”改成“矩形ABCD”，且AD＝2，CD＝4，其他条件不变．

①如图2，若PQ＝5，求AP长．

②如图3，若BD平分∠PDQ．则DP的长为        ．

18．（2022·江苏连云港期末）如图a，抛物线与x轴的一个交点为，与y轴的正半轴交于点C，顶点为D．若以AD为直径的圆经过点C．

(1)求抛物线的解析式：

(2)如图b，点E是y轴负半轴上的一点，连接BE，将绕平面内某一点旋转180°，得到（点P、M、N分别和点O、B、E对应），并且点M、N都在抛物线上，作轴于点F，若线段，求点M、N的坐标；

19．（2022·江苏盐城期末）如图，抛物线与直线交于A、B两点，其中点A在y轴上，点B的横坐标为﹣4，P为抛物线上一动点，过点P作PC垂直于AB，垂足为C，作PF垂直于x轴，垂足为F，交AB于E，设P的横坐标为t．

(1)求抛物线的解析式；

(2)①求的值；

②若点P在直线上方的抛物线上，用含t的代数式表示线段PC的长，并求线段PC取最大值时点P的坐标．

(3)若点P是抛物线上任意一点，且满足，请直接写出：

①点P的横坐标/的取值范围______；

②纵坐标为整数的点P为“玉点”，“玉点”的个数是______．

20．（2022·江苏泰州期末）已知抛物线，其中m是常数，点P是抛物线的顶点．

(1)求点P的坐标（用含m的代数式表示）；

(2)若抛物线上有且只有两个点到x轴的距离为，直接写出m的取值范围．

(3)当抛物线的顶点在第一象限时，在抛物线上有两点E(a，y1)，F(a＋3，y2)，且y1< y2，求a的取值范围．

21．（2022·江苏泰州期末）如图，线段AB是⊙O的直径，过点B作一条射线BC与AB垂直，点P是射线BC上的一个动点，连接PO交⊙O于点F，连接AF并延长交线段BP于点E，设⊙O 的半径为r，PB的长为t（t >0）．

(1)当r=3时，

①若∠FAO=∠EPF，求的长；

②若t=4，求PE的长；

(2)设PE=n2t，其中n为常数，且0<n<1，若t－r为定值，求n的值及∠EAB的度数．

22．（2022·江苏淮安期末）如图，直线与x，y轴分别交于点B，A，顶点为P的抛物线过点A．

(1)求出点A，B的坐标及c的值；

(2)若函数在时有最大值为，求a的值；

(3)若，连接AP，过点A作AP的垂线交x轴于点M．设△BMP的面积为S．

①直接写出S关于a的函数关系式及a的取值范围；

②结合S与a的函数图象，直接写出时a的取值范围．

23．（2020·江苏· 淮安市期末）如图1，在平面直角坐标系中，一次函数的图像经过点A(，m)，与y轴交于点B，与x轴交于点C．抛物线经过点A交y轴于点D(0，6)．

(1)求m的值及抛物线的表达式；

(2)如图2，点E为抛物线上一点且在直线AC上方，若EAC的面积为，求出点E的坐标；

(3)坐标轴上有一动点F，连接AF，当∠BAF=60°时，直接写出点F的坐标．

24．（2021·江苏·仪征市古井中学九年级期末）在直角坐标系中，设函数y＝ax2+bx+1（a，b是常数，a≠0）．

(1)若该函数的图象经过（1，0）和（2，1）两点，求函数的表达式，并写出函数图象的顶点坐标；

(2)已知a＝b＝1，当x＝p，q（p，q是实数，p≠q）时，该函数对应的函数值分别为P，Q．若p+q＝2，求证：P+Q＞6．

25．（2022·江苏盐城期末）如图1，在平面直角坐标系中，直线y=-6x+6与x轴、y轴分别交于A、C两点，抛物线y=x2+bx+c经过A、C两点，与x轴的另一交点为B．

(1)抛物线解析式为______；

(2)若点M为x轴下方抛物线上一动点，MN⊥x轴交BC于点N，当点M运动到某一位置时，线段MN的长度最大，求此时点M的坐标及线段MN的长度；

(3)如图2，以B为圆心、2为半径的⊙B与x轴交于E、F两点（F在E右侧），若点P是⊙B上一动点，连接PA，以PA为腰作等腰Rt△PAD，使∠PAD=90°（P、A、D三点为逆时针顺序），连接FD．

①将线段AB绕点A顺时针旋转90°，请直接写出B点的对应点B′的坐标；

②求FD长度的取值范围．

26．（2022·江苏淮安期末）已知一次函数y＝x＋4的图象与二次函数y＝ax（x－2）的图象相交于点A（－1，b）和点B，点P是线段AB上的动点（不与A、B重合），过点P作PC⊥x轴，与二次函数y＝ax（x－2）的图象交于点C．

(1)a＝        ，b＝        ，B点的坐标为        ；

(2)求线段PC长的最大值．

(3)连接AC，当△PAC是以AP为腰的等腰三角形时，直接写出点P的坐标        ．

27．（2022·江苏淮安期末）如图，抛物线y＝x2﹣2x与x轴正半轴交于点A，该抛物线的顶点为M，直线y＝﹣x+b经过点A，与y轴交于点B．

(1)b＝        ，点M的坐标为       ；

(2)将直线AB向下平移，使它经过点M，且与x轴负半轴交于点C，取点D(2，0)，连接DM，求∠DMC的度数；

(3)点E是线段AB上一动点，点F是线段OA上一动点，线段EF的延长线与线段OM交于点G．当∠BEF=2∠BAO时，是否存在点E，使得3GF=4EF？若存在，求出点E的坐标；若不存在，请说明理由．

28．（2022·江苏泰州期末）如图，在菱形ABCD中，点E在BC边上（与点B、C不重合），连接AE交BD于点G．

（1）若AG＝BG，AB＝2，BD＝3，求线段DG的长；

（2）设BC＝kBE，△BGE的面积为S，△AGD和四边形CDGE的面积分别为S1和S2，把S1和S2分别用k、S的代数式表示；

（3）求的最大值．

29．（2022·江苏南京期末）如图，⊙O是△ABC的外接圆，∠ABC＝45°，连接OC，交AB于点E．过点A作⊙O的切线，交BC的延长线于点D．

(1)求证：OC∥AD；

(2)若AE＝2，CE＝2，求⊙O的半径．

30．（2022·江苏宿迁期末）如图，在平面直角坐标系中，抛物线y＝x2+2x﹣3交y轴于点C，交x轴于点A（a，0）和点B（b，0），P是第三象限抛物线上一点，直线y＝kx+c经过P、B两点，交y轴于点D．

(1)a＝         ，b＝         ．

(2)若直线y＝kx+c上存在一点Q，以Q为圆心，QA为半径的圆恰好同时经过B、C两点，请直接写出点Q的坐标，并求k、c的值．

(3)聪明的小颖发现，若设P点的横坐标为m，则可直接得到方程x2+2x﹣3＝kx+c的解为x1＝1，x2＝m，再根与系数关系可得：，从而可得到直线PB的解析式为y＝（m+3）（x﹣1）．

①利用小颖发现的结论，当点P在抛物线的对称轴上时，直线PB的函数表达式．

②若直线AP与y轴相交于点E，是否存在常数λ，使λ•OD+OE为定值？如果存在，请求出这个定值，如果不存在，说明理由．