辽宁省抚顺市望花区2022-2023学年八年级上学期阶段练习（一）数学试题(含答案)

2022—2023学年度（上）阶段练习（一）

八年级数学

考试时间：100分钟          试卷满分：120分

一、选择题（每小题2分，共20分）

1．在中，，，则（    ）

A．50° B．60° C．70° D．80°

2．在中，，，则（    ）

A．15° B．30° C．45° D．60°

3．一个正多边形的外角与它相邻的内角之比为1:4，那么这个多边形的边数为（    ）

A．8 B．9 C．10 D．12

4．一个等腰三角形的两边长分别为6和12，则这个等腰三角形的周长为（    ）

A．30 B．24 C．18 D．24或30

5．已知三角形的两边，，第三边是，则的取值范围是（    ）

A． B． C． D．

6．如图，，，下列条件中不能判断的是（    ）

A． B． C． D．

7．如图，中，，平分，交于点，，，则的长为（    ）

A．3 B．4 C．5 D．6

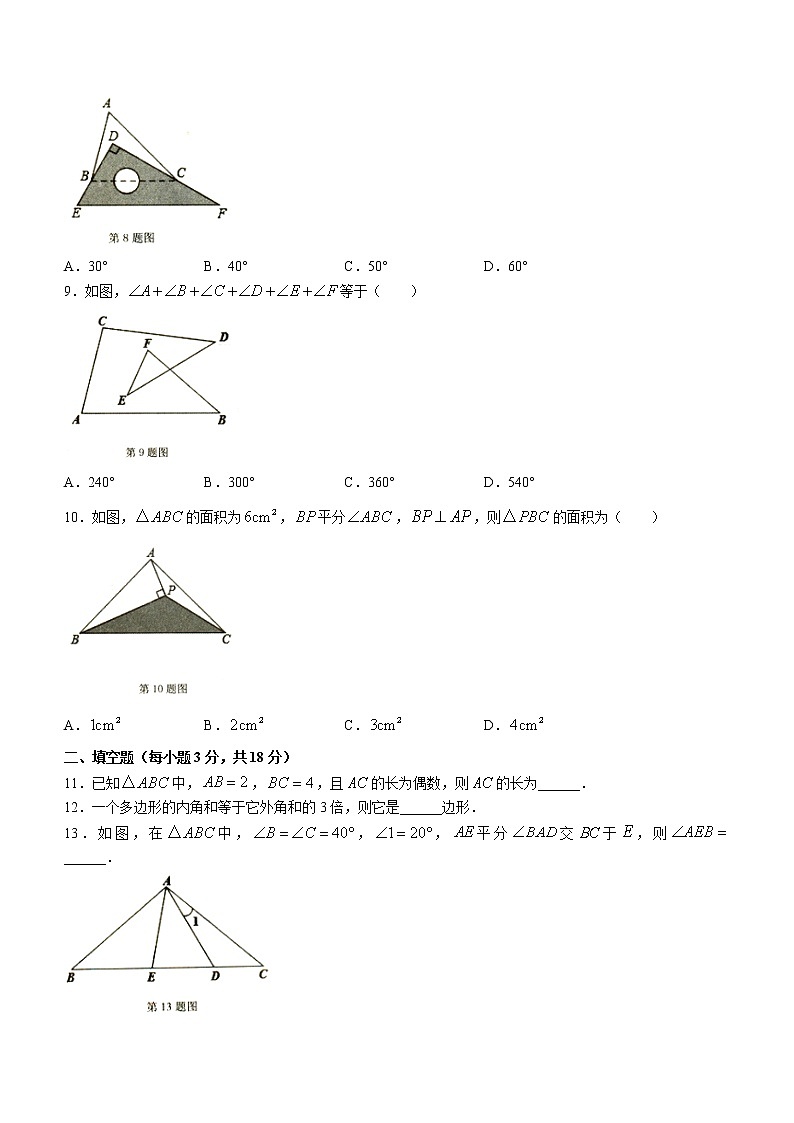
8．如图，将一块直角三角板放置在锐角上，使得该三角板的两条直角边，恰好分别经过点，．若时，点在内，则的值是（    ）

A．30° B．40° C．50° D．60°

9．如图，等于（    ）

A．240° B．300° C．360° D．540°

10．如图，的面积为，平分，，则的面积为（    ）

A． B． C． D．

二、填空题（每小题3分，共18分）

11．已知中，，，且的长为偶数，则的长为______．

12．一个多边形的内角和等于它外角和的3倍，则它是______边形．

13．如图，在中，，，平分交于，则______．

14．如图，把一张纸片沿折叠，若，，则的度数为______．

15．如图，的角平分线，相交于点，是的高，周长是20，面积为30，则______．

16．当三角形中一个内角是另一个内角的两倍时，我们称此三角形为“特征三角形”，其中称为“特征角”．如果一个“特征三角形”的一个内角为42°，那么这个“特征角”的度数为______．

三、解答题（17题8分，18题10分，共计18分）

17．在中，，，求的三个内角的度数．

18．如图，在中，，，，，垂足分别为，．

求证：

（1）；

（2）．

四、解答题（19题8分，20题8分，共计16分）

19．如图，把沿折叠，使点落在点处．

（1）若，试判断与的数量关系，并说明理由；

（2）若，求的度数．

20．如图，在和中，，，，且，，在同一直线上，连接．

（1）求证：；

（2）若，求的度数．

五、解答题（21题8分，22题10分，共计18分）

21．如图，在中，是的中点，，，垂足分别是点、，．求证：平分．

22．如图，在和中，，和相交于点，．

（1）；

（2）．

六、解答题（10分）

23．如图所示，已知，，，，交于点，交于点，判断线段，的关系并说明理由．

七、解答题（10分）

24．如图，与的角平分线交于点，与相交于点，交于点，交于．

（1）若，，求的度数；

（2）猜想，，的等量关系，直接写出结果．

八、解答题（10分）

25．如图，在和中，，，，为的中点，连接，求证：．

2022—2023学年度（上）阶段练习（一）

八年级数学参考答案

考试时间：100分钟          试卷满分：120分

   ※ 注意事项：

考生答题时，必须将答案写在答题卡上，答案写在试卷上无效．

一、选择题（每小题2分，共20分）

1．B  2．B  3．C  4．A  5．B 6．D  7．A  8．A  9．C  10．C

二、填空题（每小题3分，共18分）

11．4  12．八  13．100°  14．50° 15．3  16．42°或84°或92°

三、解答题（17题8分，18题10分，共计18分）

17． 解：∠A=x

∵∠C=∠B+20°=∠A+20°+20°=∠A+40°

∵∠A+∠B+∠C=180°，得x+x+20°+x+40°=180°

解方程得x=40°

∴ ∠A=40°，∠B=60°，∠C=80°．

18．

证明：（1）∵AD⊥CE，

∴∠ADC＝90°，

∴∠CAD+∠ACD＝90°．

∵∠BCE+∠ACD＝∠ACB=90°，

∴∠BCE＝∠CAD，

（2）∵BE⊥CE

∴∠E＝90°

又∠ADC＝90°

∴∠E=∠ADC

在△BCE和△CAD中，

∴△BCE≌△CAD（AAS）；

∴BE＝CD

四、解答题（19题8分，20题8分，共计16分）

19．

解：（1）∠1＝∠2，理由如下：

∵∠D是由∠A翻折得到，

∴∠D＝∠A，

∵DE∥AC，

∴∠1＝∠A，∠2＝∠D，

∴∠1＝∠2．

（2）∵∠A+∠B+∠C＝180°，∠A+∠AEF+∠AFE＝180°，

∴∠AEF+∠AFE＝∠B+∠C＝130°，

∵△DEF是△AEF由翻折得到，

∵∠AED＝2∠AEF，∠AFD＝2∠AFE，

∴∠AED+∠AFD＝260°，

∵∠1+∠2+∠AED+∠AFD＝360°，

∴∠1+∠2＝100°．

20．

（1）证明：∵

∴，

即

在△ABD和△ACE中

∴△ABD≌△ACE（SAS）

∴

（2）∵∠ADB+∠ADE=180°

∴∠ADB=180°-∠ADE=180°-50°=130°

又△ABD≌△ACE

∴∠ADB=∠AEC

∴∠AEC=130°

五、解答题（21题8分，22题10分，共计18分）

21．

证明：∵D是的中点，

∴，

∵，，

∴，

和中，

∴（HL）

∴，

又∵，，

∴平分线．

22．

（1）证明：在△ABO与△DCO中，

，

∴△ABO≌△DCO（ASA）

∴AB＝DC；

（2）

证明：∵△ABO≌△DCO，

∴OB＝OC，

∵OA＝OD，

∴OB＋OD＝OC＋OA，

∴BD＝AC，

在△ABC与△DCB中，

，

∴△ABC≌△DCB（SAS）．

六、解答题（10分）

23．

解：EC＝BF且EC⊥BF；理由如下

∵AE⊥AB，AF⊥AC，

∴∠BAE＝∠CAF＝90°，

∴∠BAE+∠BAC＝∠CAF+∠BAC，

∴∠EAC＝∠BAF，

在△ABF和△AEC中，

，

∴△ABF≌△AEC（SAS），

∴EC＝BF，∠AEC＝∠ABF

∵AE⊥AB，

∴∠BAE＝90°，

∴∠AEC+∠ADE＝90°，

∵∠ADE＝∠BDM（对顶角相等），

∴∠ABF+∠BDM＝90°，

在△BDM中，∠BMD＝180°﹣∠ABF﹣∠BDM＝90°，

∴EC⊥BF．

∴EC＝BF且EC⊥BF

七、解答题（10分）

24．

解：（1）设∠CAD＝2x，∠CBD＝2y，

由∠CAD和∠CBD的角平分线相交于点P可知：

∠CAP＝∠PAD＝x，∠CBP＝∠DBP＝y，

∵三角形的内角和等于180°，∠C＝35°，∠D＝29°，

∴∠C+∠CAD+∠AOC＝∠D+∠CBD+∠BOD，

又∠AOC＝∠BOD

∴∠C+∠CAD＝∠D+∠CBD

即35°+2x＝29°+2y①．

∵∠AEB是△APE与△DBE的外角，

∴∠P+∠EAP＝∠D+∠DBP，即∠P+x＝29°+y②．

同理，∵∠AFB是△ACF与△BFP的外角，

∴∠C+∠CAP＝∠P+∠CBP，即35°+x＝∠P+y③，

①﹣②得，y＝x+35°﹣∠P④，

①﹣③得，x＝y+29°﹣∠P⑤，

④代入⑤得，x＝x+35°﹣∠P+29°﹣∠P，

2∠P＝35°+29°，

解得∠P＝32°；

（2）∠P＝（∠C+∠D）

八、解答题（10分）

25．

 证明：延长AF到G，使FG=AF，连接BG

∴AG=2AF

∵F为BE的中点

∴FE=FG

在△BFG和△EFA中

∴△BFG≌△EFA （SAS）

∴GB=AE ，∠FGB＝∠FAE

∴AE∥BG

∴  ∠ABG+∠BAE=180°

  又

∴

 ∴ ∠ABG= ∠CAD

又AD=AE

∴AD=GB

在△ABG和△CAD中

∴ △ABG≌△CAD（SAS）

∴AG=CD

∴CD=2AF