中职人教版5 电磁感应课文配套课件ppt

这是一份中职人教版5 电磁感应课文配套课件ppt，共60页。PPT课件主要包含了电磁波谱，“恒反抗”等内容，欢迎下载使用。

法拉第 （Michael Faraday, 1791-1867），伟大的英国物理学家和化学家. 他创造性地提出场的思想 ，磁场这一名称是法拉第最早引入的 . 他是电磁理论的创始人之一 ，于1831年发现电磁感应现象，后又相继发现电解定律，物质的抗磁性和顺磁性，以及光的偏振面在磁场中的旋转.
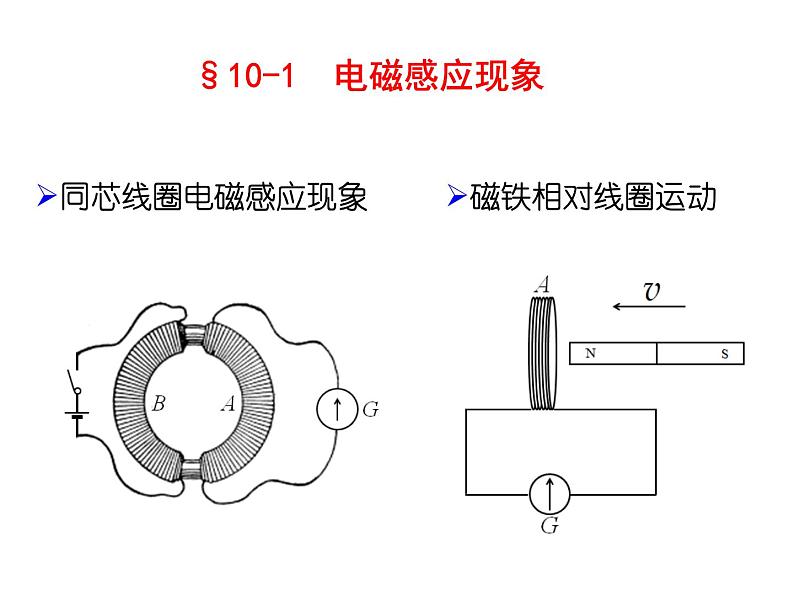
§10-1 电磁感应现象
§10-2 动生电动势和感生电动势
动生电动势——由于导体相对磁场运动而产生的感应电动势；
感生电动势——由于磁感强度大小或（和）方向发生变化而产生的感应电动势。
产生感应电流的装置虽然非常多，但是按着产生感应电动势的机制不同，我们可以把感应电动势分成两类：动生电动势和感生电动势。
动生电动势的洛仑兹力解释
在磁感强度 的磁场中，长L 的导线以速度 向右运动，每个电子受到的洛仑兹力为
在洛仑兹力作用下，电子向O端漂移。
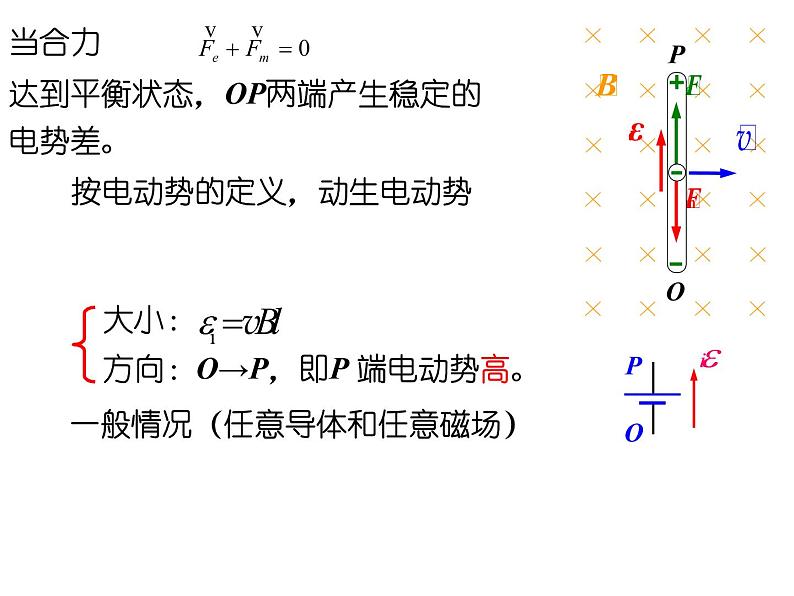
达到平衡状态，OP两端产生稳定的电势差。
按电动势的定义，动生电动势
方向：O→P，即P 端电动势高。
一般情况（任意导体和任意磁场）
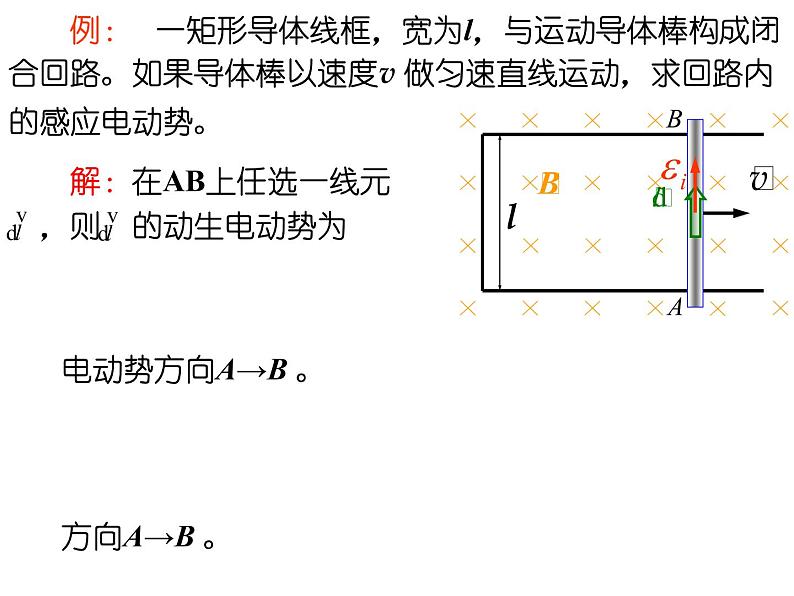
例： 一矩形导体线框，宽为l，与运动导体棒构成闭合回路。如果导体棒以速度v 做匀速直线运动，求回路内的感应电动势。
解：在AB上任选一线元 ，则 的动生电动势为
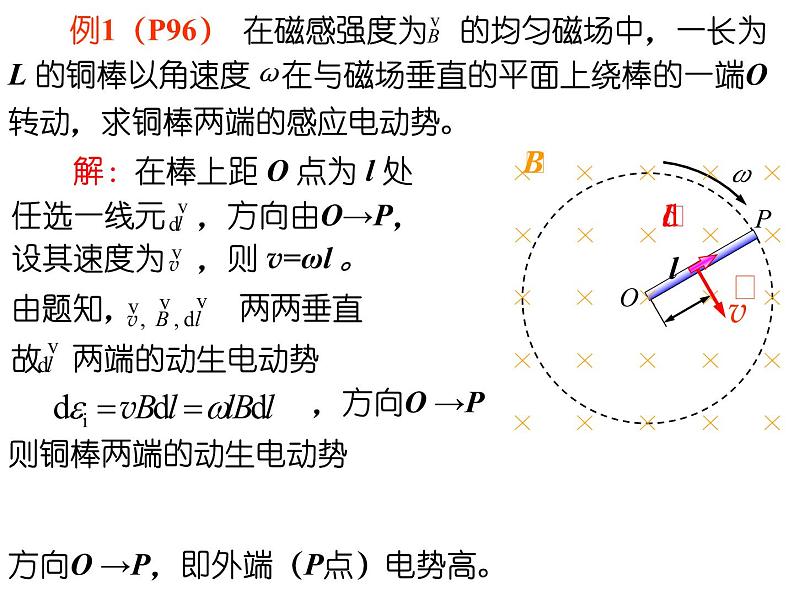
例1（P96） 在磁感强度为 的均匀磁场中，一长为 L 的铜棒以角速度ω在与磁场垂直的平面上绕棒的一端O转动，求铜棒两端的感应电动势。
解：在棒上距 O 点为 l 处任选一线元 ，方向由O→P，设其速度为 ，则 v=ωl 。
则铜棒两端的动生电动势
方向O →P，即外端（P点）电势高。
如图所示，当磁感应强度B发生变化时，可观察到电流计的指针发生偏转，即在闭合导线框中有感应电动势产生，从而在回路中有感应电流。像这样不是由于导线相对磁场运动，而是由于磁场的变化在闭合回路中产生的感应电动势叫做感生电动势。
洛仑兹力解释不了感生电动势；
Maxwell 假说——涡旋电场。
涡旋电场与静电场有本质不同：
静电场：自由电荷激发，电力线有头尾，场的环流为零；
涡电场：变化磁场激发，电力线闭合的，环流不恒为零；
相同点是：对电荷都作用。
例2（P97）有一半径为r，电阻为R 的细圆环，放在与圆环所围的平面相垂直的均匀磁场中。设磁场的磁感强度随时间变化，且dB/dt = 常量。求圆环上的感应电流的值。
解：按题意，感生电动势
当穿过闭合回路所围面积的磁通量发生变化时，回路中会产生感应电动势，且感应电动势正比于磁通量对时间变化率的负值.
§10-3 电磁感应定律
式中的负号的与感应电动势的方向有关。
感应电动势的方向
我们规定如图所示闭合回路的正绕向，用右手螺旋定则判断出线圈平面的正法线方向 。
例： 一矩形导体线框，宽为l，与运动导体棒构成闭合回路。如果导体棒以速度v 做匀速直线运动，用电磁感应定律求回路内的感应电动势。
解：根据法拉第电磁感应定律
1）闭合回路由 N 匝密绕线圈组成
2）若闭合回路的电阻为 R ，感应电流为
在匀强磁场中匀速转动的线圈内的感应电流是时间的正弦函数 . 这种电流称交流电.
§10-4 楞次定律
闭合回路中的感应电流方向除了可用上一节电磁感应定律的方法进行判断之外，还可以用楞次定律更加快捷的判断，两种方法是等效的。楞次定律可表述为：
闭合回路中感应电流的方向总是使它所激发的磁场来阻止引起该感应电流的磁通量的变化。
感应电流的效果，总是反抗引起感应电流的原因。
用楞次定律判断感应电流方向
例： 一矩形导体线框，宽为l，与运动导体棒构成闭合回路。如果导体棒以速度v 做匀速直线运动。用楞次定律判断感应电流方向。
楞次定律是能量守恒定律的一种表现
维持滑杆运动必须外加一力，此过程为外力克服安培力做功转化为焦耳热.
在不能视为线状的连续导体中产生的感应电流。
金属导体，R 小（ρ 小），I f 很大；
I f ∝ ω , —— 高频炉，矽钢片；
I f ∝ R -1 , —— 铁淦氧，硅钢片；
I f 与 I 反相, —— 电磁阻尼，瓦时计，磁悬浮，异步电机；
趋肤效应，—— 表面硬化，空心导线；
例如铜和铝，可产生涡流现象，但不宜用作电磁炉的锅。
如图所示，回路1中的电流发生变化时，在回路2中产生感应电动势，这种现象称为互感应现象，该电动势称为互感电动势。
§10-6 互感和自感
根据毕-萨-拉定律，由回路1 中的电流I1 激发的在回路2 处的磁场B21穿过回路2 的磁链数
式中M12和M21由两回路的形状、大小、匝数和相对位置决定，还与它们所在空间介质的性质有关。
无铁磁性物质存在时， M12 和M21与回路电流无关。
互感系数SI制单位: Ｈ， Wb·A-1， V·s·A-1
回路本身不变两回路相对位置及空间介质不变无铁磁物质存在
M12和M21—— 互感系数，简称互感。
M 的定义：可用下两式之一定义
M 的计算：可用上两式之一计算。
例1：图中线圈1 匝密度n , 线圈2匝数N , 两线圈同轴，截面积S , 求两线圈的互感系数M。
例2 两长度为l、半径分别为r1、r2，匝数分别为N1、N2的同轴长直密绕螺线管，求它们的互感。
解：设通过半径为r1的螺线管的电流为I，则该螺线管内的磁感强度
则穿过半径为r2的线圈的磁链
应用： 变压器，互感器，感应电动机，· · ·
害处： 串扰，分布参数，噪声与损耗，· · ·
回路电流发生变化时，其激发的磁场穿过回路自身的磁通量亦随之发生变化，则在回路中产生感应电动势，这种现象称为自感应现象，该电动势称为自感电动势。
式中L 是自感系数，简称自感，由回路的形状、大小、匝数和空间介质的性质决定。
无铁磁性物质存在时， L 与回路电流无关。
回路本身不变空间介质不变无铁磁物质存在
L 的定义：可用下两式之一定义
L 的计算：可用上两式之一计算。
例3：螺线管的自感（电感）
例：在长为60cm，直径为5.0cm的空心纸筒上绕多少匝线圈才能得到自感为6.0×10-3 H的线圈？
解：已知线圈的长度为l，半径为d，自感为L。设一共需要绕N匝，空心纸筒的磁导率μ可以近似地看作真空中的磁导率μ0
应用：镇流器，扼（抑）流圈，谐振电路，· · ·
害处：上电迟延，断电影响，分布参数，· · ·
电场具有能量，电场的能量储存在场不为零的空中；如电容器电场中的能量为
§10-7 磁场的能量 磁场能量密度
同样，磁场也具有能量，磁场的能量储存于磁场不为零的空间。
现利用RL电路讨论磁场的能量。
注：由电阻R和线圈L组成的电路称为RL电路。
RL电路：电阻为R，电感为L ，电源电动势为ε。
电键未闭合时，电路中没有电流，线圈内也没有磁场；
闭合电键后，线圈中电流逐渐增大，线圈产生自感电动势，方向与ε相反，反抗电流变化。
有电感的电路中，为了克服自感电动势，电源需要提供更多能量，这部分能量则转换成电感的磁场能量。
纯电阻电路中，电源提供的能量只转换成电阻上的焦耳热能。
设t = 0时，I = 0；任意t 时刻，电流增大到 I 。对上式积分，可得
电源反抗自感电动势所作的功
设长直螺线管体积为V，自感为L =μn2V 。当通有电流 I 时，螺线管内的磁感强度
对于各向同性的均匀介质，B = μH ，则磁场能量密度还可写为
对各向同性的均匀介质，磁场能量还可写为
例1 有一长0.20m、截面积 S =5.0cm2 的长直螺线管。当螺线管通以电流 I=450mA时，螺线管可储存磁场能量Wm=0.10J。试问此长直螺线管需绕多少匝线圈？
解：已知，长直螺线管的自感
例2* 如图同轴电缆，中间充以磁介质，芯线与圆筒上的电流大小相等、方向相反。已知R1，R2，I 和μ，求单位长度同轴电缆的磁能和自感。（金属芯线内的磁场可忽略）
解：同轴电缆芯线内的磁场强度不计，电缆外的磁场强度为零，由安培环路定律可求出
磁介质中的磁场能量密度
则单位长度同轴电缆的磁场能量
L 的计算：可用以上三式之一计算。
L 的定义：可按下列三式之一定义
3. 磁场的能量密度
恒定磁场中的安培环路定理
上式表明，真空中磁场强度的环流等于穿过回路面积的传导电流的代数和。
在有电容的电路中，传导电流是不连续的，安培环路定理遇到困难！
§10-8 电磁场与电磁波
当安培定理应用于L时，对于曲面S1，因有传导电流穿过该面，有
对于曲面S2，因没有传导电流穿过该面，有
因为电容器的存在，对于同一个闭合回路L，得到了两种不同的结果。
Maxwell假说——位移电流：
真空中某点的位移电流密度等于该点电位移矢量对时间的变化率；
通过电场中某一截面的位移电流等于通过该截面电位移通量对时间的变化率。
真空中静电场与恒定磁场的基本方程
二 麦克斯韦方程组的积分形式
电场的环路定理修正为
真空中安培环路定理修正为
静电场中的高斯定理和恒定磁场中的高斯定理，也适用于一般电磁场。
麦克斯韦方程组的积分形式
位移电流可存在于导体、介质及真空中；
与束缚电荷的运动相关。
Ic 与 Id 比较：
存在导体、介质及真空中；
存在于导体中 也可存在于介质中
真空中可以有光存在，可以有场存在。
变化电场激发磁场，右螺旋
变化磁场激发电场，左螺旋
图12.2 电磁场互激
变化电场激发涡旋磁场,
变化磁场激发涡旋电场,
电场与磁场密切联系着。
静电场与稳恒磁场只是电磁场在一定条件下的特殊形式。
1864年麦克斯韦预言了电磁波的存在，并且计算出电磁波的波速等于光速。他还由此提出光的电磁理论，认为光是以波动形式传播的一种电磁振动。与机械波不同，电磁波的传播不依赖于介质，可以在真空中传播，因为电磁波的传播靠的是电场和磁场的相互“激发”，而电场和磁场本身就是物质的一种形式。
1886年，赫兹利用振荡器与谐振器在实验中证实了电磁波的存在。
振荡电路 无阻尼自由电磁振荡
电容C 和电感L组成的电路称为LC 振荡电路，简称振荡电路。
极板的电势差U0等于电源的电动势E，极板A、B所带电荷量分别为Q0 和-Q0；
将S 接入电动势为E 的电源，电源对电容器C 充电，使电容器两
再将S 与自感线圈相接。 此后，将不断重复电容对电感放电和电感对电容充电的过程；即产生电磁振荡。电磁振荡也是电能和磁能不断转换的过程。
最简单的LC 回路：只有一个电感和一个电容组成；
理想LC 振荡电路：回路总电阻=0（可忽略不计），
——无阻尼自由振荡电路。
广义的电磁辐射包括无线电波、微波、红外线、可见光、X 射线、γ 射线等。对无线电波（kHz ~ MHz）而言，可用振荡电路产生电磁振荡。
当电阻很小时，可采用直流供电，在电路中产生受迫电磁振荡。再满足一定条件，就可将电磁能量辐射出去。
按Maxwell电磁理论，交变电场在周围空间激发出磁场，交变磁场在周围空间激发出涡旋电场。如此，电磁场即可由此及彼地传播出去。
上述无阻尼自由振荡电路是理想化的，实际中只可能尽量降低回路的电阻，总有焦耳热能损耗。
电路开放（天线）：参见下图。
所以，L、C 必须足小。
（由Maxwell方程组可导出）
振荡的电偶极子可以产生电磁波。在真空中，离开电偶极子很远的地方，电场强度的波面及磁场强度的波面趋于平面，就形成平面电磁波。平面电磁波的波函数与平面简谐波的形式相同，为：
电磁波的存在，是横波；
光是一种电磁波，真空中光速
可见光的波长范围： 400 nm～ 760 nm
2. 感生电场与静电场的区别
七. 磁场的能量 磁场能量密度
八.麦克斯韦方程组的积分形式
九.真空中的平面电磁波