2022年广东省深圳市南山区某校中考数学模拟试卷（4月份）

这是一份2022年广东省深圳市南山区某校中考数学模拟试卷（4月份），共38页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）在一次数学活动课上，老师将1～10共十个整数依次写在十张不透明的卡片上（每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下）．他先打乱这些卡片的顺序，然后把甲、乙、丙、丁、戊五位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己的两张卡片上的数字之和写在黑板上，结果分别是：甲12、乙4、丙15、丁6、戊18．根据以上信息，判断错误的是（ ）
A．丙同学的两张卡片上的数字是7和8
B．戊同学的两张卡片上的数字是8和10
C．丁同学的两张卡片上的数字是2和4
D．甲同学的两张卡片上的数字是5和7
2．（3分）2021年11月8日至11日，党的十九届六中全会在北京召开．全会审议通过的《中共中央关于党的百年奋斗重大成就和历史经验的决议》，聚焦总结党的百年奋斗重大成就和历史经验，突出中国特色社会主义新时代这个重点．体现了党中央对党的百年奋斗的新认识，是一篇光辉的马克思主义纲领性文献，是新时代中国共产党人牢记初心使命、坚持和发展中国特色社会主义的政治宣言，是以史为鉴、开创未来、实现中华民族伟大复兴的行动指南．如图为“百年奋斗成就”展示在正方体的展开图上，则“奋”的相对面是（ ）
A．百B．斗C．成D．就
3．（3分）要使式子有意义，则q的取值范围是（ ）
A．q＝7B．q≥7C．q≤7D．q≠7
4．（3分）我们定义：如图，在△ABC中，把AB绕点A顺时针旋转α（0°＜α＜180°）并缩短一半得到AB'，把AC绕点A逆时针旋转β并缩短一半得到AC'，连接B'C'．当α+β＝180°时，我们称△AB'C'是△ABC的“旋半三角形”，△AB'C'边B'C'上的中线AD叫做△ABC的“旋半中线”，点A叫做“旋半中心”．在平面直角坐标系中，△ABC的坐标分别是A（4，3），B（1，0），C（5，0），△AB′C′是△ABC的“旋半三角形”，AD是△ABC的“旋半中线”，连接OD，求OD的最大值，并且写出当OD最大时点D的坐标（ ）
A．
B．
C．
D．
5．（3分）对于平面直角坐标系xOy中第一象限内的点P（x，y）和图形W，给出如下定义：过点P作x轴和y轴的垂线，垂足分别为M，N，若图形W中的任意一点Q（a，b）满足a≤x且b≤y，则称四边形PMON是图形W的一个覆盖，点P为这个覆盖的一个特征点．例：若M（1，3），N（4，3），则点P（5，4）为线段MN的一个覆盖的特征点．已知A（1，4），B（4，1），C（2，4）．若在一次函数y＝mx+6（m≠0）的图象上存在△ABC的覆盖的特征点，得出m的取值范围是（ ）
A．m≥﹣0.5且m≠0B．m≤﹣0.5且m≠0
C．m≥﹣0.5D．m≠﹣0.5且x＜﹣5
6．（3分）某商品现在的售价为每件35元，每天可卖出50件．市场调查反映：如果调整价格，每降价1元，每天可多卖出2件．请你帮助分析，当每件商品降价多少元时，可使每天的销售额最大，求最大销售额是（ ）
A．2500元B．2000元C．1800元D．2200元
7．（3分）一个点到圆的最小距离为3cm，最大距离为6cm，则该圆的直径是（ ）
A．1.5cmB．1.5cm或4.5cm
C．4.5cmD．3cm或9cm
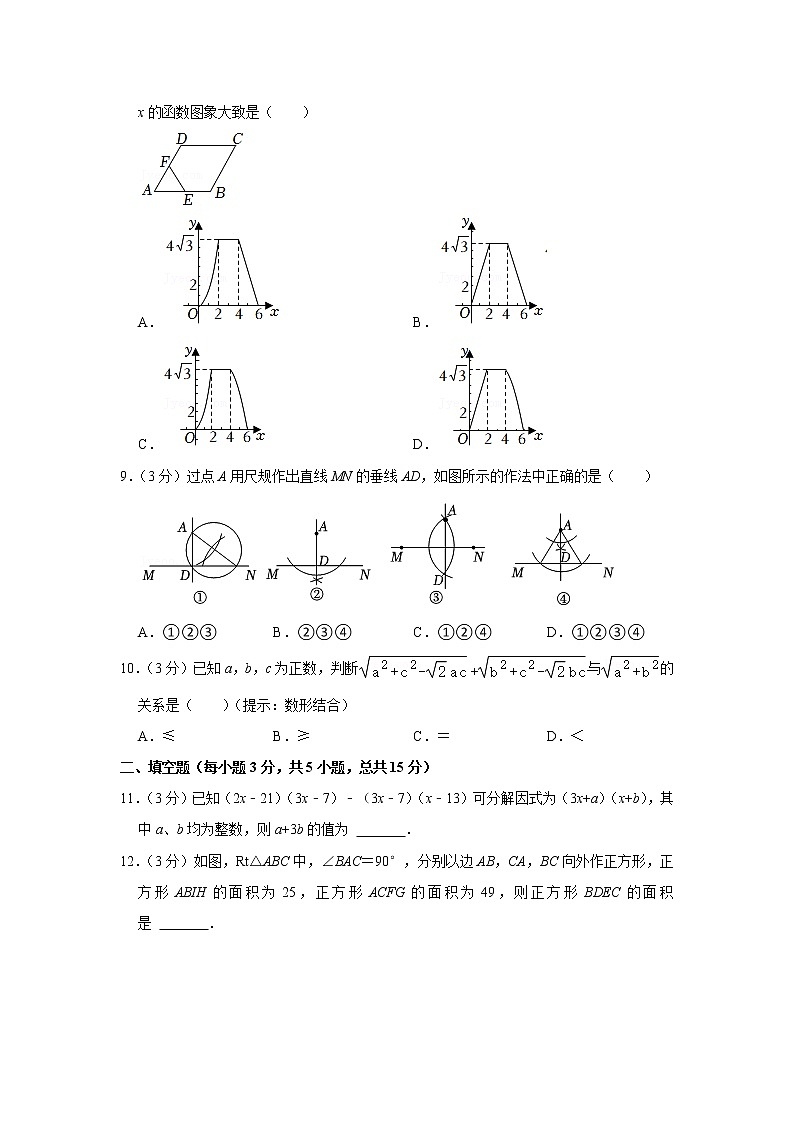
8．（3分）如图，已知菱形ABCD的边长为4，∠A＝60°，动点E从A开始，以每秒2个单位的速度沿路径A—B—C—D移动，动点F从点A开始，以每秒2个单位的速度沿路径A—D移动，F点到达终点D点后停下来不动，另一个动点继续向终点D点移动，直至终点D才停下来，设点E移动的时间为x（单位：s），△AEF的面积记为y，则y关于x的函数图象大致是（ ）
A．B．
C．D．
9．（3分）过点A用尺规作出直线MN的垂线AD，如图所示的作法中正确的是（ ）
A．①②③B．②③④C．①②④D．①②③④
10．（3分）已知a，b，c为正数，判断与的关系是（ ）（提示：数形结合）
A．≤B．≥C．＝D．＜
二、填空题（每小题3分，共5小题，总共15分）
11．（3分）已知（2x﹣21）（3x﹣7）﹣（3x﹣7）（x﹣13）可分解因式为（3x+a）（x+b），其中a、b均为整数，则a+3b的值为 ．
12．（3分）如图，Rt△ABC中，∠BAC＝90°，分别以边AB，CA，BC向外作正方形，正方形ABIH的面积为25，正方形ACFG的面积为49，则正方形BDEC的面积是 ．
13．（3分）设7﹣的整数部分为h，小数部分为j，求得（2h+）j的值为 ．
14．（3分）如图，点P为矩形ABCD外部一点，已知PA＝PC＝3，若PD＝1，则AC的取值范围为 ．
15．（3分）如图，在△ABC纸板中，AC＝8，BC＝4，AB＝10，P是AC上一点，过点P沿直线剪下一个与△ABC相似的小三角形纸板，如果有4种不同的剪法，那么AP长的取值范围是 ．
三、解答题（本题总分55分，其中16题6分，17题6分，18题7分，19题8分，20题9分，21题9分，22题10分）
16．（6分）化简求值：，其中，n＝5m．
17．（6分）数学课上，同学们对王老师黑板上的题很感兴趣，他们答案都不同，且众说纷纭．题目如下：
化简：
①小浩说：当a，b，c皆为正数时，化简结果为；
②小特说：当a，b，c皆为负数时，化简结果为；
③小凌说：当a＜0，b＞0，c＜0时，化简结果为；
④小斯说：当a＞0，b＜0，c＜0时，化简结果为；
（1）以上同学的说法正确的是 （双选）；
（2）请在这四个中任选两个判断其正确性．
18．（7分）某校学生会为了解该校2860名学生喜欢球类活动的情况，采取抽样调查的办法，从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好，并将调查的结果绘制成两幅不完整的统计图（如图（1），图（2），要求每位同学只能选择一种自己喜欢的球类；图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数），请你根据图中提供的信息，解答下列问题：
（1）在这次研究中，一共调查了 名学生．
（2）喜欢排球的人数在扇形统计图中所占的圆心角是 度．
（3）补全频数分布折线统计图．
（4）估计该校喜欢排球的学生有多少人？
19．（8分）如图，在△ABC中，BE平分∠ABC交AC于点E，点D在BC上，连接AD交BE于点H，且∠DAB＝∠C，BH＝BD，过点H作HF∥BC交AC于点F，BG⊥AD交AC于点G．
（1）求证：△ABD∽△CBA．
（2）若AE＝6，EF＝2，求GF的长度．
20．（9分）某商店销售一款口罩，每袋的进价为12元，计划售价大于12元但不超过20元，且售价为整数元．
（1）经市场调查发现，当售价为每袋18元时，日均销售量为50袋，每袋售价每增加1元，日均销售量减少5袋．售价定为每袋多少元时，所得日均毛利润最大？最大日均毛利润为多少元？
（2）疫情期间，该商店分两批共购进2万袋同款口罩，进价不变．该商店将购进的第一批口罩a袋（8000≤a≤11200）做“买一送一”的促销活动，第二批口罩没有做促销活动，且这两批的售价相同．若这2万袋口罩全部售出后的总利润率为20%，则每袋口罩的售价可能是多少元？（毛利润＝售价﹣进价，利润率＝毛利润÷进价）
21．（9分）我们知道：如图①，点B把线段AC分成两部分，如果＝，那么称点B为线段AC的黄金分割点．它们的比值为．
（1）在图①中，若AC＝20cm，则AB的长为 cm；
（2）如图②，用边长为20cm的正方形纸片进行如下操作：对折正方形ABCD得折痕EF，连接CE，将CB折叠到CE上，点B对应点H，得折痕CG．试说明：G是AB的黄金分割点；
（3）如图③，小明进一步探究：在边长为a的正方形ABCD的边AD上任取点E（AE＞DE），连接BE，作CF⊥BE，交AB于点F，延长EF、CB交于点P．他发现当PB与BC满足某种关系时，E、F恰好分别是AD、AB的黄金分割点．请猜想小明的发现，并说明理由．
22．（10分）已知抛物线y＝ax2+bx+c（a﹣1不为整数）的顶点D（，），AB⊥BC．
（1）直接得出抛物线解析式．
（2）如图1所示，点P为抛物线一动点，∠PBC＝3∠ABO，求xP；
（3）如图2，延长DB交x轴于点E，EF平分∠BEO，交线段AB于点F．x轴正半轴有一点S，且AS＝12EF．过点F作FG∥x轴，交抛物线的对称轴于点G．该对称轴交x轴于点H．过点G作线段IM、NQ，且NH＝MH＝IH＝QH．线段IQ交直线FG于点R，若线段MN恰好交FG于点F．那么请求出R点坐标．并试问∠EFA与∠RSE是否存在倍数关系？若存在，请分别求出它们的角度大小并写出存在的倍数关系；若不存在，请说明理由．
2022年广东省深圳市南山区某校中考数学模拟试卷（4月份）
参考答案与试题解析
一、单项选择题（每小题3分，共10小题，总共30分）
1．（3分）在一次数学活动课上，老师将1～10共十个整数依次写在十张不透明的卡片上（每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下）．他先打乱这些卡片的顺序，然后把甲、乙、丙、丁、戊五位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己的两张卡片上的数字之和写在黑板上，结果分别是：甲12、乙4、丙15、丁6、戊18．根据以上信息，判断错误的是（ ）
A．丙同学的两张卡片上的数字是7和8
B．戊同学的两张卡片上的数字是8和10
C．丁同学的两张卡片上的数字是2和4
D．甲同学的两张卡片上的数字是5和7
【分析】根据有理数的加法先确定出乙同学的数字，然后依次确定丁，甲，丙，戊同学的数字即可．
【解答】解：乙同学是1，3；
丁同学是2，4；
甲同学是5，7；
丙同学是6，9；
戊同学是8，10；
故选：A．
【点评】本题考查了有理数的加法，解题关键是熟练掌握有理数加法法则，注意数字不重复．
2．（3分）2021年11月8日至11日，党的十九届六中全会在北京召开．全会审议通过的《中共中央关于党的百年奋斗重大成就和历史经验的决议》，聚焦总结党的百年奋斗重大成就和历史经验，突出中国特色社会主义新时代这个重点．体现了党中央对党的百年奋斗的新认识，是一篇光辉的马克思主义纲领性文献，是新时代中国共产党人牢记初心使命、坚持和发展中国特色社会主义的政治宣言，是以史为鉴、开创未来、实现中华民族伟大复兴的行动指南．如图为“百年奋斗成就”展示在正方体的展开图上，则“奋”的相对面是（ ）
A．百B．斗C．成D．就
【分析】根据正方体的表面展开图找相对面的方法，“Z”字两端是对面，判断即可．
【解答】解：在正方体的展开图上，则“奋”的相对面是就，
故选：D．
【点评】本题考查了正方体相对两个面上的文字，熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键．
3．（3分）要使式子有意义，则q的取值范围是（ ）
A．q＝7B．q≥7C．q≤7D．q≠7
【分析】根据二次根式有意义的条件列不等式求解．
【解答】解：由题意可得：2q﹣14≥0，
解得：q≥7，
故选：B．
【点评】本题考查二次根式有意义的条件，理解二次根式有意义的条件（被开方数为非负数）是解题关键．
4．（3分）我们定义：如图，在△ABC中，把AB绕点A顺时针旋转α（0°＜α＜180°）并缩短一半得到AB'，把AC绕点A逆时针旋转β并缩短一半得到AC'，连接B'C'．当α+β＝180°时，我们称△AB'C'是△ABC的“旋半三角形”，△AB'C'边B'C'上的中线AD叫做△ABC的“旋半中线”，点A叫做“旋半中心”．在平面直角坐标系中，△ABC的坐标分别是A（4，3），B（1，0），C（5，0），△AB′C′是△ABC的“旋半三角形”，AD是△ABC的“旋半中线”，连接OD，求OD的最大值，并且写出当OD最大时点D的坐标（ ）
A．
B．
C．
D．
【分析】如图4中，先确定OD最大值时，D的位置，D在以A为圆心，以1为半径的圆上，则当D运动到直线OA与半圆相交时OD最大，求此时OD的长并确定其坐标．
【解答】解：首先证明结论AD＝BC．
理由：如图1中，延长AD到M，使得AD＝DM，连接B′M，C′M，
∵B′D＝DC′，AD＝DM，
∴四边形AC′MB′是平行四边形，
∴AC′＝B′M＝2AC，
∵∠BAC+∠B′AC′＝180°，∠B′AC′+∠AB′M＝180°，
∴∠BAC＝∠MB′A，
∵AB＝2AB′，
∴△BAC∽△AB′M，
∴BC＝2AM，
∴AD＝BC．
如图，∵A（4，3），B（1，0），C（5，0），
∴OA＝5，OB＝1，OC＝5
∵AD＝BC，BC＝4，
∴AD＝1，
∴D在以A为圆心，以1为半径的圆上，
∴当D运动到直线OA与半圆相交时OD最大，
∵A（4，3），
∴OA＝5，
∵AD＝1，
∴OD的最大值是6．
过A作AE⊥x轴于E，过D作DF⊥x轴于F，
∴AE∥DF，
∴△AOE∽△DOF，
∴＝＝＝，
∵OE＝4，AE＝3，
∴OF＝，DF＝，
∴D（，）．
故选：A．
【点评】主要考查了新定义“旋半三角形”和“旋半中线”、全等三角形的判定和性质、平行四边形的判定和性质、直角三角形30度角性质、等边三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．
5．（3分）对于平面直角坐标系xOy中第一象限内的点P（x，y）和图形W，给出如下定义：过点P作x轴和y轴的垂线，垂足分别为M，N，若图形W中的任意一点Q（a，b）满足a≤x且b≤y，则称四边形PMON是图形W的一个覆盖，点P为这个覆盖的一个特征点．例：若M（1，3），N（4，3），则点P（5，4）为线段MN的一个覆盖的特征点．已知A（1，4），B（4，1），C（2，4）．若在一次函数y＝mx+6（m≠0）的图象上存在△ABC的覆盖的特征点，得出m的取值范围是（ ）
A．m≥﹣0.5且m≠0B．m≤﹣0.5且m≠0
C．m≥﹣0.5D．m≠﹣0.5且x＜﹣5
【分析】当m＞0时，符合题意；当m＜0时，当x≥4且y≥4时，P（x，y）为△ABC的覆盖特征点，当直线y＝mx+6过点（4，4）时，求出m＝﹣是m的临界值；则可求m的取值范围为m≥﹣且m≠0．
【解答】解：①当m＞0时，符合题意；
②当m＜0时，当x≥4且y≥4时，P（x，y）为△ABC的覆盖特征点，
∵点P在一次函数y＝mx+6上，
∴当直线y＝mx+6过点（4，4）时，
4＝4m+6，
∴m＝﹣，
∴﹣≤m＜0，
综上所述：m≥﹣且m≠0．
故选：A．
【点评】本题考查新定义，理解题意，根据所给条件，确定是△ABC的覆盖特征点的特征是解题的关键．
6．（3分）某商品现在的售价为每件35元，每天可卖出50件．市场调查反映：如果调整价格，每降价1元，每天可多卖出2件．请你帮助分析，当每件商品降价多少元时，可使每天的销售额最大，求最大销售额是（ ）
A．2500元B．2000元C．1800元D．2200元
【分析】设每件商品降价x元，每天的销售额为y元，由题意可得到y和x的二次函数关系，利用配方法可求最值．
【解答】解：设每件商品降价x元，每天的销售额为y元．
依题意有：y＝（35﹣x）（50+2x）＝﹣2x2+20x+1750＝﹣2（x﹣5）2+1800，
∵﹣2＜0，
∴当x＝5时，y最大，最大值为1800，
∴最大销售额为1800元．
故选：C．
【点评】本题考查二次函数的应用，利用数学知识解决实际问题，解题的关键是建立函数模型，利用配方法求最值．
7．（3分）一个点到圆的最小距离为3cm，最大距离为6cm，则该圆的直径是（ ）
A．1.5cmB．1.5cm或4.5cm
C．4.5cmD．3cm或9cm
【分析】分类讨论：分点在圆外或点在圆内进行讨论．
【解答】解：当点在圆外，则该圆的直径＝6cm﹣3cm＝3cm；当点在圆内，则该圆的直径＝6cm+3cm＝9cm，
即该圆的直径为3cm或9cm．
故选：D．
【点评】本题考查了点与圆的位置关系：设⊙O的半径为r，点P到圆心的距离OP＝d，则有：点P在圆外⇔d＞r；点P在圆上⇔d＝r；点P在圆内⇔d＜r．
8．（3分）如图，已知菱形ABCD的边长为4，∠A＝60°，动点E从A开始，以每秒2个单位的速度沿路径A—B—C—D移动，动点F从点A开始，以每秒2个单位的速度沿路径A—D移动，F点到达终点D点后停下来不动，另一个动点继续向终点D点移动，直至终点D才停下来，设点E移动的时间为x（单位：s），△AEF的面积记为y，则y关于x的函数图象大致是（ ）
A．B．
C．D．
【分析】根据题意可知，需要分三种情况：当点E在线段AB上时，当点E在线段BC上时，当点E在线段CD上时，分别求出对应的函数关系式，再判断图象即可．
【解答】解：当点E在线段AB上时，点F在AD上，此时0＜x＜2时，
此时y＝•（2x）2＝x2，由此可排除B，D；
当点E在线段BC上时，点F与点D重合，
此时y＝×4×＝4；
当点E在线段CD上时，点F与点D重合，
此时y＝×2×（12﹣x）＝﹣+12，此时函数图象是一段一次函数图象，由此可排除C，
故选：A．
【点评】本题主要考查动点问题的函数图象问题，关键是根据点的运动求出对应函数解析式．
9．（3分）过点A用尺规作出直线MN的垂线AD，如图所示的作法中正确的是（ ）
A．①②③B．②③④C．①②④D．①②③④
【分析】①根据直径所对的圆周角是直角判断即可；
②③根据基本作图判断即可；
④根据等腰三角形的三线合一的性质判断即可．
【解答】解：图①中，由圆周角定理可知，∠ADN＝90°，符合题意．
图②中，由作图可知AD⊥MN，符合题意．
图③中，由作图可知MN垂直平分线段AD，符合题意．
图④中，根据等腰三角形三线合一的性质可知AD⊥MN，符合题意，
故选：D．
【点评】本题考查作图﹣复杂作图，垂线等知识，解题的关键是熟练掌握五种基本作图，属于中考常考题型．
10．（3分）已知a，b，c为正数，判断与的关系是（ ）（提示：数形结合）
A．≤B．≥C．＝D．＜
【分析】利用数形结合法，画出几何图形，利用勾股定理和余弦定理解答即可．
【解答】解：作MB⊥BN，BP平分∠MBN，取BA＝a，BC＝b，BD＝c，连接AC，BD，AD，CD，如图，
∵AB⊥BC，
∴AC＝＝．
∵BP平分∠MBN，
∴∠ABD＝∠CBD＝45°．
由余弦定理得：
AD＝＝，
CD＝＝，
∵AD+CD≥AC，
∴≥．
故选：B．
【点评】本题主要考查了二次根式的性质，勾股定理，余弦定理，利用数形结合的思想，利用几何图形解答是解题的关键．
二、填空题（每小题3分，共5小题，总共15分）
11．（3分）已知（2x﹣21）（3x﹣7）﹣（3x﹣7）（x﹣13）可分解因式为（3x+a）（x+b），其中a、b均为整数，则a+3b的值为 ﹣31 ．
【分析】直接提取公因式（3x﹣7），进而合并同类项得出即可．
【解答】解：（2x﹣21）（3x﹣7）﹣（3x﹣7）（x﹣13）
＝（3x﹣7）（2x﹣21﹣x+13）
＝（3x﹣7）（x﹣8），
∵（2x﹣21）（3x﹣7）﹣（3x﹣7）（x﹣13）可分解因式为（3x+a）（x+b），
∴（3x﹣7）（x﹣8）＝（3x+a）（x+b），
则a＝﹣7，b＝﹣8，
故a+3b＝﹣7+3×（﹣8）
＝﹣31．
故答案为：﹣31．
【点评】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．
12．（3分）如图，Rt△ABC中，∠BAC＝90°，分别以边AB，CA，BC向外作正方形，正方形ABIH的面积为25，正方形ACFG的面积为49，则正方形BDEC的面积是 74 ．
【分析】根据勾股定理得AB2+AC2＝BC2，将AB2＝25，AC2＝144代入即可求得正方形BDEC的面积．
【解答】解：在Rt△ABC中，∠BAC＝90°，
由勾股定理得：AB2+AC2＝BC2，
∵正方形ABIH的面积为25，正方形ACFG的面积为49，
∴AB2＝25，AC2＝49，
∴BC2＝AB2+AC2＝25+49＝74，
∴正方形BDEC的面积为BC2＝74．
故答案为：74．
【点评】本题主要考查了勾股定理和正方形面积的表示，熟记勾股定理是解题的关键，属于基础题．
13．（3分）设7﹣的整数部分为h，小数部分为j，求得（2h+）j的值为 4﹣21 ．
【分析】先估算出的值，从而求出h，j的值，再把h，j的值代入式子中进行计算即可解答．
【解答】解：∵25＜33＜36，
∴5＜＜6，
∴﹣6＜﹣＜﹣5，
∴1＜7﹣＜2，
∴7﹣的整数部分为1，小数部分为7﹣﹣1，
∴h＝1，j＝6﹣，
∴（2h+）j
＝（2×1+）×（6﹣）
＝（2+）×（6﹣）
＝12﹣2+6﹣33
＝4﹣21，
故答案为：4﹣21．
【点评】本题考查了估算无理数的大小，二次根式的混合运算，准确熟练地进行计算是解题的关键．
14．（3分）如图，点P为矩形ABCD外部一点，已知PA＝PC＝3，若PD＝1，则AC的取值范围为 ﹣1≤AC＜2 ．
【分析】连接BD交AC于O，连接PO，由矩形的性质可得AC＝BD，AO＝CO＝BO＝DO，由三角形中线与三角形三边关系，可求PB的长，由三角形的三边关系可求解．
【解答】解：如图，连接BD交AC于O，连接PO，
∵四边形ABCD是矩形，
∴AC＝BD，AO＝CO＝BO＝DO，
∵PO是△ACP的中线，也是△PBD的中线，
∴PA2+PC2＝2（AO2+PO2），PB2+PD2＝2（PO2+OD2），
∴PA2+PC2＝PB2+PD2，
∴9+9＝1+PB2，
∴PB＝，
在△PBD中，﹣1≤BD≤+1，
∴﹣1≤AC≤+1，
当点P在AD上时，CD＝＝＝2，
∴AC＝＝＝2，
故答案为：﹣1≤AC＜2．
【点评】本题考查了矩形的性质，三角形的三边关系及勾股定理，正确作出辅助线是解决本题的关键．
15．（3分）如图，在△ABC纸板中，AC＝8，BC＝4，AB＝10，P是AC上一点，过点P沿直线剪下一个与△ABC相似的小三角形纸板，如果有4种不同的剪法，那么AP长的取值范围是 6≤AP＜8 ．
【分析】分四种情况讨论，依据相似三角形的对应边成比例，即可得到AP的长的取值范围．
【解答】解：如图所示，过P作PD∥AB交BC于D或PE∥BC交AB于E，则△PCD∽△ACB或△APE∽△ACB，
此时0＜AP＜8；
如图所示，过P作∠APF＝∠B交AB于F，则△APF∽△ABC，
此时0＜AP≤8；
如图所示，过P作∠CPG＝∠CBA交BC于G，则△CPG∽△CBA，
此时，△CPG∽△CBA，
当点G与点B重合时，CB2＝CP×CA，即42＝CP×8，
∴CP＝2，AP＝6，
∴此时，6≤AP＜8；
综上所述，要有4种不同的剪法，使得过点P沿直线剪下一个与△ABC相似，则AP长的取值范围是6≤AP＜8．
故答案为：6≤AP＜8．
【点评】本题主要考查了相似三角形的判定，相似三角形的对应角相等，对应边的比相等，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．
三、解答题（本题总分55分，其中16题6分，17题6分，18题7分，19题8分，20题9分，21题9分，22题10分）
16．（6分）化简求值：，其中，n＝5m．
【分析】先化简分式，再将m，n的值代入计算．
【解答】解：∵
＝﹣••
＝﹣，
∴当，n＝5m时，
原式＝﹣
＝﹣．
【点评】此题考查了分式化简并求值的能力，关键是能进行准确的计算、化简．
17．（6分）数学课上，同学们对王老师黑板上的题很感兴趣，他们答案都不同，且众说纷纭．题目如下：
化简：
①小浩说：当a，b，c皆为正数时，化简结果为；
②小特说：当a，b，c皆为负数时，化简结果为；
③小凌说：当a＜0，b＞0，c＜0时，化简结果为；
④小斯说：当a＞0，b＜0，c＜0时，化简结果为；
（1）以上同学的说法正确的是 ①③④ （双选）；
（2）请在这四个中任选两个判断其正确性．
【分析】根据二次根式的性质化简计算即可．
【解答】解：①当a，b，c皆为正数时，原式＝++
＝++
＝．
故①正确．
②当a，b，c皆为负数时，0，无意义，
∴②错误．
③当a＜0，b＞0，c＜0时，原式＝++
＝++
＝
＝．
∴③正确．
④当a＞0，b＜0，c＜0时，原式＝++
＝+
＝
＝．
∴①③④正确．
故答案为：①③④．
（2）选①②判断如下：
①当a，b，c皆为正数时，原式＝++
＝++
＝．
故①正确．
②当a，b，c皆为负数时，0，无意义，
∴②错误．
【点评】本题考查二次根式的性质和计算，掌握相关法则是求解本题的关键．
18．（7分）某校学生会为了解该校2860名学生喜欢球类活动的情况，采取抽样调查的办法，从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好，并将调查的结果绘制成两幅不完整的统计图（如图（1），图（2），要求每位同学只能选择一种自己喜欢的球类；图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数），请你根据图中提供的信息，解答下列问题：
（1）在这次研究中，一共调查了 100 名学生．
（2）喜欢排球的人数在扇形统计图中所占的圆心角是 36 度．
（3）补全频数分布折线统计图．
（4）估计该校喜欢排球的学生有多少人？
【分析】（1）根据乒乓球的人数和所占的百分比，即可求出总人数；
（2）根据（1）求出的总人数和喜欢篮球的人数所占的百分比，求出喜欢篮球的人数，从而得出喜欢排球的人数，用喜欢排球的人数除以总人数，再乘以
360度，即可求出喜欢排球的人数在扇形统计图中所占的圆心角；
（3）根据总人数求出各个喜欢球的人数所占的百分比，从而补全统计图；
（4）根据喜欢排球所占的百分比，再乘以全校的总人数，即可求出答案．
【解答】解：（1）一共调查的总人数是：20÷20%＝100（名）；
故答案为：100．
（2）根据（1）得：喜欢篮球的人数是：100×40%＝40（名），
则喜欢排球的人数是：100﹣30﹣20﹣40＝10（名），
喜欢排球的人数在扇形统计图中所占的圆心角是×360°＝36°；
故答案为：36．
（3）足球的所占的百分比是：×100%＝30%，
排球所占的百分比是：×100%＝10%，
补图如下：
（4）根据题意得：
2860×＝286（人），
答：全校学生中最喜欢排球的学生约有286人．
【点评】本题考查了折线统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比，折线统计图表示的是事物的变化情况．
19．（8分）如图，在△ABC中，BE平分∠ABC交AC于点E，点D在BC上，连接AD交BE于点H，且∠DAB＝∠C，BH＝BD，过点H作HF∥BC交AC于点F，BG⊥AD交AC于点G．
（1）求证：△ABD∽△CBA．
（2）若AE＝6，EF＝2，求GF的长度．
【分析】（1）根据角平分线的性质及相似三角形的判定可得出结论；
（2）延长HF、BG交于点P，利用角平分线及相似三角形的判定与性质可得∠ADB＝∠CAB，再三次运用相似三角形的判定与性质可得BD＝BH＝9，设BP与DH交于点M，过点H作HQ∥PG交EF于Q，根据角平分线定义及相似三角形的性质可得出比例线段，最后根据ASA得△PFG≌△HFQ，由全等三角形的性质可得答案．
【解答】（1）证明：∵BE平分∠ABC，
∴∠ABE＝∠CBE，
∵∠DAB＝∠C，∠DBA＝∠ABC，
∴△ABD∽△CBA；
（2）解：∵△ABD∽△CBA，
∴∠ADB＝∠CAB，
∵BD＝BH，
∴∠CAB＝∠ADB＝∠BHD＝∠EHA，
∴△EHA∽△EAB，
∴∠EAH＝∠EBA＝∠CBE，
∴△EAH～DBH，
∵HF∥BC，
∴∠EHF＝∠EBC＝∠EAH，
∴△FEH∽△FHA，
∴，，
∴FH＝＝4，
∴EH＝•HA＝×6＝3，
∵∠EBA＝∠EAH，
∴△EAH∽△EBA，
∴，
∴EB＝＝12，
∴BH＝EB﹣EH＝9，
∴BD＝BH＝9，
设BP与DH交于点M，
∵HP∥BD，
∴∠HPM＝∠DBM，∠PHM＝∠BDM，
∴△HPM∽△DBM，
∴，
∵BD＝BH，BM⊥DH，
∴BM平分HD，
∴＝1，HP＝BD＝9，
∴PF＝HP﹣HF＝4，
过点H作HQ∥PG交EF于Q，
∴∠QHF＝∠EPG＝∠PBD＝∠HBD＝∠EHF，
∴HQ是△EHF内角∠EHF的角平分线，
∴存在，
∴FQ＝•EF＝，
在△PFG和△HFQ中，
，
∴△PFG≌△HFQ（ASA），
∴GF＝FQ＝．
【点评】此题考查的是全等三角形的判定与性质、相似三角形的判定与性质、角平分线的定义等知识，正确作辅助线构造相似三角形是解决此题关键．
20．（9分）某商店销售一款口罩，每袋的进价为12元，计划售价大于12元但不超过20元，且售价为整数元．
（1）经市场调查发现，当售价为每袋18元时，日均销售量为50袋，每袋售价每增加1元，日均销售量减少5袋．售价定为每袋多少元时，所得日均毛利润最大？最大日均毛利润为多少元？
（2）疫情期间，该商店分两批共购进2万袋同款口罩，进价不变．该商店将购进的第一批口罩a袋（8000≤a≤11200）做“买一送一”的促销活动，第二批口罩没有做促销活动，且这两批的售价相同．若这2万袋口罩全部售出后的总利润率为20%，则每袋口罩的售价可能是多少元？（毛利润＝售价﹣进价，利润率＝毛利润÷进价）
【分析】（1）根据题意列出函数解析式即可，再根据二次函数的性质确定函数的最值；
（2）根据商店获得利润以及售出的袋数求出每袋利润，再根据a的取值范围，求出定价．
【解答】解：（1）设每袋口罩的销售价格为x元，所得日均毛利润为y元，
由题意可得：
y＝（x﹣12）[50﹣5（x﹣18）]＝﹣5x2+200x﹣1680＝﹣5（x﹣20）2+320＝﹣5（x﹣20）2+320，
∵﹣5＜0，
∴当x＝20时，y有最大值320，
∴当销售价格定为每袋20元时，所得日均毛利润最大，最大日均毛利润为320元；
（2）由题意知这批口罩的利润为：20000×12×20%＝48000（元），
第一批口罩a袋，第二批口罩（20000﹣a）袋，
设每袋口罩的售价为m元，则am+（20000﹣a）m﹣12×20000＝48000，
∴m＝，
∵8000≤a≤11200，
∴18≤m≤20，
∵m为整数，
∴每袋口罩的价格可能为18元或19元或20元．
【点评】本题主要考查二次函数的应用，关键是根据题意列出函数关系式并掌握二次函数的性质．
21．（9分）我们知道：如图①，点B把线段AC分成两部分，如果＝，那么称点B为线段AC的黄金分割点．它们的比值为．
（1）在图①中，若AC＝20cm，则AB的长为 （10） cm；
（2）如图②，用边长为20cm的正方形纸片进行如下操作：对折正方形ABCD得折痕EF，连接CE，将CB折叠到CE上，点B对应点H，得折痕CG．试说明：G是AB的黄金分割点；
（3）如图③，小明进一步探究：在边长为a的正方形ABCD的边AD上任取点E（AE＞DE），连接BE，作CF⊥BE，交AB于点F，延长EF、CB交于点P．他发现当PB与BC满足某种关系时，E、F恰好分别是AD、AB的黄金分割点．请猜想小明的发现，并说明理由．
【分析】（1）由黄金分割点的概定义可得出答案；
（2）延长EA，CG交于点M，由折叠的性质可知，∠ECM＝∠BCG，得出∠EMC＝∠ECM，则EM＝EC，根据勾股定理求出CE的长，由锐角三角函数的定义可出tan∠BCG＝，即，则可得出答案；
（3）证明△ABE≌△BCF（ASA），由全等三角形的性质得出BF＝AE，证明△AEF∽△BPF，得出，则可得出答案．
【解答】解：（1）∵点B为线段AC的黄金分割点，AC＝20cm，
∴AB＝×20＝（10﹣10）cm．
故答案为：（10﹣10）．
（2）延长EA，CG交于点M，
∵四边形ABCD为正方形，
∴DM∥BC，
∴∠EMC＝∠BCG，
由折叠的性质可知，∠ECM＝∠BCG，
∴∠EMC＝∠ECM，
∴EM＝EC，
∵DE＝10，DC＝20，
∴EC＝＝＝10，
∴EM＝10，
∴DM＝10+10，
∴tan∠DMC＝＝．
∴tan∠BCG＝，
即，
∵AB＝BC，
∴，
∴G是AB的黄金分割点；
（3）当BP＝BC时，满足题意．
理由如下：
∵四边形ABCD是正方形，
∴AB＝BC，∠BAE＝∠CBF＝90°，
∵BE⊥CF，
∴∠ABE+∠CFB＝90°，
又∵∠BCF+∠BFC＝90°，
∴∠BCF＝∠ABE，
∴△ABE≌△BCF（ASA），
∴BF＝AE，
∵AD∥CP，
∴△AEF∽△BPF，
∴，
当E、F恰好分别是AD、AB的黄金分割点时，
∵AE＞DE，
∴，
∵BF＝AE，AB＝BC，
∴，
∴，
∴BP＝BC．
【点评】本题是相似形综合题，考查了翻折变换的性质，正方形的性质，全等三角形的判定和性质，黄金分割点的定义，锐角三角函数，相似三角形的判定与性质等知识，熟练掌握相似三角形的判定与性质是解题的关键．
22．（10分）已知抛物线y＝ax2+bx+c（a﹣1不为整数）的顶点D（，），AB⊥BC．
（1）直接得出抛物线解析式．
（2）如图1所示，点P为抛物线一动点，∠PBC＝3∠ABO，求xP；
（3）如图2，延长DB交x轴于点E，EF平分∠BEO，交线段AB于点F．x轴正半轴有一点S，且AS＝12EF．过点F作FG∥x轴，交抛物线的对称轴于点G．该对称轴交x轴于点H．过点G作线段IM、NQ，且NH＝MH＝IH＝QH．线段IQ交直线FG于点R，若线段MN恰好交FG于点F．那么请求出R点坐标．并试问∠EFA与∠RSE是否存在倍数关系？若存在，请分别求出它们的角度大小并写出存在的倍数关系；若不存在，请说明理由．
【分析】（1）根据顶点写出抛物线的顶点式，再根据AB⊥BC得出OB2＝OA•OC，再转化为a和c的关系，解出a，b，c，最后得到抛物线解析式；
（2）由上一问将∠ABO转化为∠BCO，从而得到点P的两种可能：第一种，在x轴上构造两次等腰三角形从而得到∠3∠BCO，再延长 与抛物线的新交点即为P点；第二种，过点B作x轴平行线，构造∠∠BCO，再在 上再构造2∠BCO即可得到3∠BCO，此时的角的边延长与抛物线的新交点即为P点；
先根据点D，点B得出直线DB，再得出点E坐标，再根据EF平分∠BEO得出F点坐标，EF的长以及EF与y轴坐标 （为了之后方便求∠EFA做准备），再用 AS＝12EF算出S点坐标；接着根据G点与H点的做法得出 FG以及G点坐标；根据NH＝MH＝IH＝QH得出点N，M，I，Q都在以H为圆心的圆上；延长FG后根据HGFG得出点G是弦的中点，于是本题即为著名的“蝴蝶定理”——点G也是FR的中点，得出R的坐标；最后根据之前的准备与各点的坐标算出∠RSE＝135°，∠EFA＝45°，∠RSE＝3∠EFA．
【解答】解：（1）如图1，设点A（x1，0），C（x2，0）
由题意，a≠0，其中x1，x2 是一元二次方程ax2+bx+c＝0的两个根
∵抛物线y＝ax2+bx+c的顶点为D（，），
可设抛物线的顶点式为y+a（x﹣）2+，即y+ax2﹣3ax+，
∴与抛物线的一般式y＝ax2+bx+c对比，得，
当x＝0时，相应的抛物线的函数值为c，
点B坐标为（0，C），
∵AB⊥BC，
∴∠ABC＝90°，
∴∠OBA+∠OBC＝90°，
∵∠OAB+∠OBA＝90°，
∴∠OAB＝∠OBC，
∵∠AOB＝∠BOC，
∴△OAB∽△OBC，
∴∠ABO＝∠BCO，＝，
∴OA2＝OB•OC，
如图1中，点A（x1，0）在y轴左侧，点C（x2，0）在y轴右侧，点B（0，c）在y轴正半轴，
∴OA＝﹣x1，OB＝OC＝，OC＝x2，其中c＞0，即＞0，
∴a＞﹣，
将以上数值代入到OB2＝OA•OC中，得c2＝﹣x1x2，
又x1，x2是一元二次方程ax2+bx+c＝0的两个根，
∴x1x2＝，
∴c2＝﹣，
∴ac＝﹣1，
∴a•＝﹣1，
∴a＝﹣或﹣，
∵a﹣1不为整数，而（﹣）﹣1＝﹣2为整数，
∴a＝﹣舍去，
抛物线的解析式为y＝﹣x2+x+；
（2）如图1中，
∵在第（1）问中已证∠ABO＝∠BCO，
∴条件变为∠PBC＝3∠BCO，
在第（1）问中已求出抛物线的解析式为y＝﹣x2+x+，
∴x1，x2是方程﹣x2+x+＝0的两根，
∴x1＝﹣，x2＝，
∴A（﹣，0），B（0，），C（，0），
满足∠PBC＝3∠BCO的抛物线上的动点P一共有两种情形：
第一种，如下图所示，连接BC，作线段BC的垂直平分线交x轴于B1点，连接BB1，再作线段BB1的垂直平分线交x轴于B2点，连接BB2，
∴BB1＝B1C，BB2＝B2B1，
∴∠BCB1＝∠B1BC，∠BB1B2＝∠B2BB1，
∵∠BB1B2＝∠BCB1+∠B1BC＝2∠BCB1，即∠BB1O＝2∠BCO，
∴∠B2B1C＝∠B2BB1+∠B1BC＝∠BB1B2+∠BCB1＝2∠BCB1+∠BCB1＝3∠BCB1，
又点B1，O都在x轴上，∠BCB1＝∠BCO，
∴∠B2BC＝3∠BCO，
∴点P只需为直BB2与抛物线的另一个交点即可，此时∠PBC＝∠B2BC＝3∠BCO，符合题目要求，如下图所示；所以只需求出点B2的坐标，再得出直BB2的解析式，最后得出点P横坐标
∵∠BOC＝∠BOB1＝∠BOB2＝90°，B（0，），C（），BB1＝B1C，
∴OB＝，OC＝，OB1＝OC﹣B1C＝﹣BB1，
在Rt△BOB1中，（BB1）2＝OB2+OB12＝（）2+（﹣BB1）2，
∴BB1＝，
∴B1C＝BB1＝，OB1＝﹣BB1＝，
∴OB2＝OB1﹣B2B1＝﹣BB2，
在Rt△BOB2中，B2B2＝OB2+B2O2＝（）2+（﹣B2B）2，
∴B2B＝，
∴B2B2＝BB2＝，OB2＝﹣BB2＝，
∴点B2的坐标为（，0），
设直线BB2的解析式为y＝kx+t1，
∴，解方程组得，
直线BB2的解析式为y＝﹣x+，
由，
解得x＝0或，
∴满足条件的点P的横坐标为．
第二种，如图1，过点B作关于抛物线对称轴对称的点B3，点B3仍在抛物线上；再连接BB3，将线段BB3绕着点B逆时针旋转到BB4，使得∠B4BB3＝2∠BCO；过点B4作B4B5⊥BB3于B5，
∵BB3∥x轴，且B3（3，），BB3＝3，
∴∠BCO＝∠B3BC，
∵∠B4BB3＝2∠BCO，
∴∠B4BC＝∠B4BB3+∠B3BC＝2∠BO+∠BCO＝3∠BCO，
又∵此时∠PBC＝∠B4BC，
∴∠PBC＝3∠BCO符合题意，
根据作法，BB4＝BB3＝3，且在第一种情形已知∠BB1O＝2∠BCO，OB＝，OB1＝，
∴∠B4BB3＝2∠BCO＝∠BB1O，
∴tan∠B4BB3＝tan∠BB1O＝＝＝，
在Rt△B4B5B中，＝tan∠B4BB3＝，
∴B4B5＝BB5，
在Rt△B4B5B中，BB42＝BB52+B4B52，
∴32＝BB52+（BB5）2
∴BB5＝，B4B5＝，
∴B4（，）
∴直线BB4的解析式为y＝x+，
由，
解得x＝或0，
∴满足条件的点P的横坐标为，
综上所述，满足条件的点P的横坐标为或．
（3）结论：∠RSE＝3∠EFA．
理由：∵点D（，），点B（0，），
∴直线BD的解析式为y＝x+，
∴点E（﹣，0），
∴OE＝，OB＝
根据勾股定理，BE＝＝，
如图3，延长EF交y轴于点F1，过点F1作F1F2⊥BE于点F2，
∵EF平分∠BEO，
∴EF1平分∠BEO，且OF1＝F1F2（角平分线上的点到角的两边距离相等），
∵•BF1•OE＝•BE•F1F2，
即（OB﹣OF1）•OE＝BE•OF1，
∴（﹣OF1）×＝•OF1，
∴OF1＝，
∴F1（0，），
∴直线EF的解析式为y＝x+，
∵A（﹣，0），B（0，），
∴直线AB的解析式为y＝3x+，
由，解得，
∴F（﹣，），
∵E（﹣，0），
∴EF＝，
∵x轴正半轴有一点S，且AS＝12EF，
∴AS＝12×，
∴AS＝，
∵A（﹣，0），
∴S（3，0），
∵FG∥x轴，交抛物线于点G，对称轴交X轴于点H，
∴HG⊥FG，G（，），
∵NH＝MH＝IH＝QH，
点I，Q，M，N在以H为圆心，以HI为半径的圆上，
为方便，将圆中相关部分单独提出，并将直线FG两端延长至与⊙H相交，F侧交点记为F′，R侧交点记为R′，如图2所示，
∴FN•FM＝FF′•FR′，IR•QR＝RR′•RF′，
过点R作MN的平行线交NQ于点K，交MI的延长线于点L，
∴∠M＝∠L，∠N＝∠GKR，
∵∠FGM＝∠LGR，∠NGF＝∠KGR，
∴△FGM∽△LGR，△NGF∽△KGR，
∴＝，＝，
∴＝，
∵∠L＝∠M＝∠Q，∠IRL＝∠QRK，
∴△ILR∽△KQR，
∴＝即LR•KR＝IR•QR，
∴＝，即＝，
∵F′G＝GR′，
∴＝，
∴＝，
∴﹣1＝﹣1，
∴FG＝RG，
∴点G也是FR的中点，
∴R（，），
如图3，过点F1作F1F3⊥AB于点F3，过点R作RR1⊥x轴于点R1．
∵R（，），S（3，0），F1（0，），
∴R1（，0），SR1＝﹣3＝，
∴RR1＝SR1，
∴△RR1S是等腰直角三角形，
∴∠RSR1＝45°，
∴∠RSE＝180°﹣45°＝135°，
∴∠EFA＝∠F1FF3，
∵F（﹣，），F1（0，），
∴FF1＝，
∵∠ABP＝∠F1BF3，∠AOB＝∠F1F3B＝90°，
∴△F1F3B∽△ABO，
∴＝，
∴＝，
∴F1F3＝，
∴sin∠F1FF3＝＝，
∴∠F1FF3＝45°，
∴∠EFA＝45°，
∴∠RSE＝3∠EFA．
【点评】本题综合考查一次函数、二次函数、相似三角形、等腰三角形、勾股定理、三角函数的概念、角平分线性质、圆的性质等知识点，尤其第（3）问考查了著名的平面几何定理——“蝴蝶定理”，这拓宽了考生的知识面，提高了考生的解题能力；第（2）问考查中难题里的倍角问题，考生应掌握如何构造等腰三角形来处理倍角问题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/8/19 0:34:44；用户：初中数学；邮箱：sxljy01@xyh.cm；学号：24425668