




还剩24页未读,
继续阅读
初中数学苏科版九年级下册7.6 用锐角三角函数解决问题教学课件ppt
展开
这是一份初中数学苏科版九年级下册7.6 用锐角三角函数解决问题教学课件ppt,共32页。PPT课件主要包含了复习引入,三角函数,坡角问题,ihl,如图AB是一斜坡,俯角问题,由上往下拍摄,水下仰拍,由下往上拍摄,方向角问题等内容,欢迎下载使用。
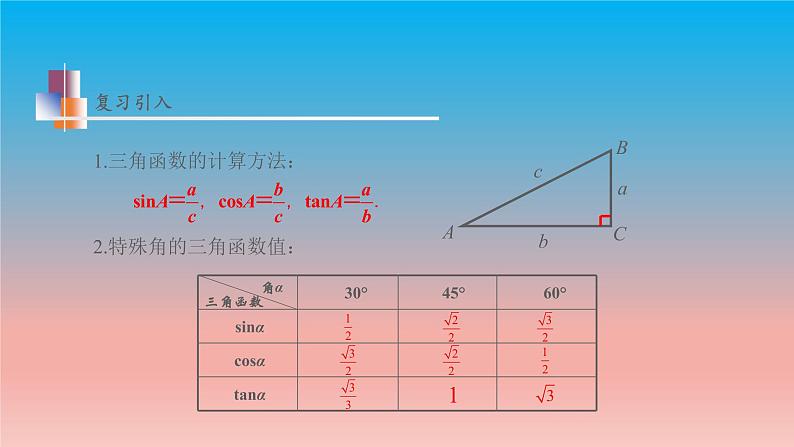
1.三角函数的计算方法:
2.特殊角的三角函数值:
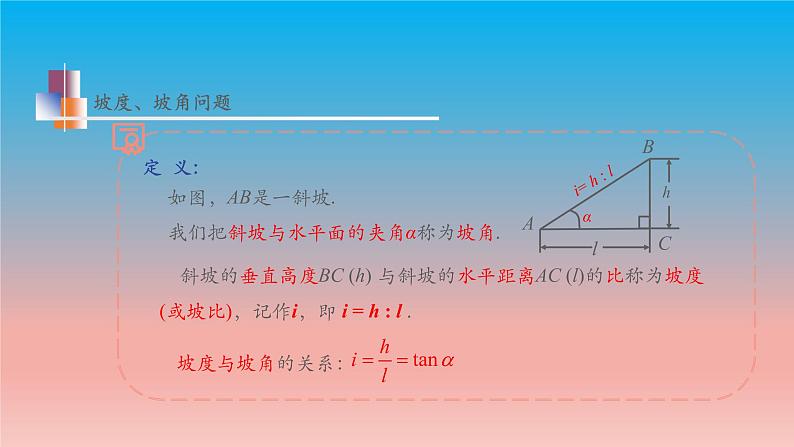
我们把斜坡与水平面的夹角α称为坡角.
斜坡的垂直高度BC (h) 与斜坡的水平距离AC (l)的比称为坡度 (或坡比),记作i,即 i = h : l .
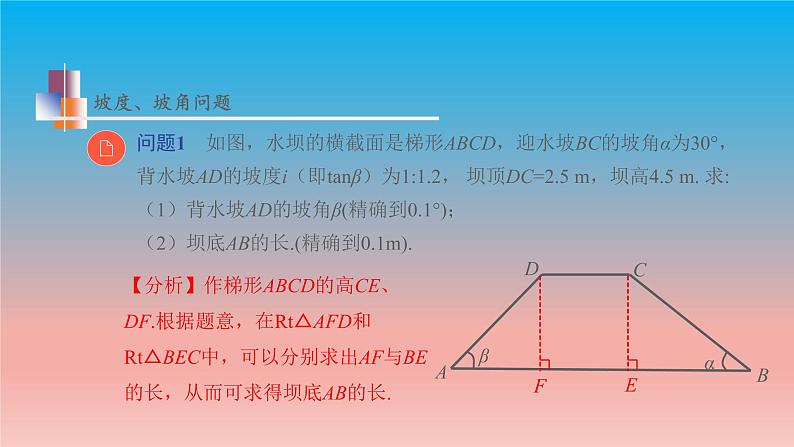
【分析】作梯形ABCD的高CE、DF.根据题意,在Rt△AFD和Rt△BEC中,可以分别求出AF与BE的长,从而可求得坝底AB的长.
解:如图,作CE⊥AB,DF⊥AB,垂足分别为E、F.
用计算器计算,得β ≈ 39. 8.
(2)在Rt△BEC中,α = 30°,∠BCE= 90°-30°= 60°, EB = CE·tan∠BCE = 4.5× tan 60°.
∴AF= 1.2DF = 1.2×4.5= 5.4.
又FE= DC= 2.5,
∴AB = AF+FE+EB= 5.4+2.5+4.5×tan60°≈15.7.
我们在观察物体时,视线与水平线所成的角称为仰角或俯角.
从上往下看,视线与水平线的夹角叫做俯角.
右图中的∠1就是________, ∠2就是________.
从下往上看,视线与水平线的夹角叫仰角.
解:如图,α = 30°,β= 60°, AD=120.
∴BD=AD· tana =120· tan30°
CD=AD· tanβ =120· tan60°
因此,这栋楼高约为277.1m.
解:如图 ,在Rt△APC中,
PC=PA·cs(90°-65°)
=80×cs25°≈80×0.91=72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130n mile.
用锐角三角函数解决实际问题
【分析】如图,用⊙O表示摩天轮,小明从底部点A出发,经过2 min后到达点B,由题意可求∠BOA的大小.如果作BC⊥OA,垂足为C,在Rt△OCB中,可以根据OB及∠BOA的大小求得OC,那么就可知道此时小明离地面的高度.
解:如图,用⊙O表示摩天轮,A、B分别表示小明的出发点和2 min后的到达点.由题意知,OB= 20,∠BOA = 360°÷6= 60°.作BC⊥OA,垂足为C.在Rt△OCB中,
答:2 min后小明离地面10. 3 m.
AC = AO-CO= 20-10= 10.因为摩天轮底部与地面相距0.3 m,所以小明离地面的高度应为10.3 m.
2.小亮为测量如图所示的湖面的宽度BC,他在同一水平面上取一点A,测得湖的一端C在A处的正北方向,另一端B在A处的北偏东60°的方向,并测得A,C间的距离AC=10 m,则湖的宽度BC为________m.
3.某水库堤坝的横断面如图所示,迎水坡AB的坡度是1∶3,堤坝高BC=50 m,则AB=_______m.
5.某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯. 如图,已知原阶梯式自动扶梯AB长为10 m,坡角∠ABD=30°,改造后的斜坡式自动扶梯的坡角∠ACB=15°,请你计算改造后的斜坡式自动扶梯AC的长度.(结果精确到0.1 m,参考数据:sin15°≈0.26,cs15°≈0.97,tan15°≈0.27)
答:改造后的斜坡式自动扶梯AC的长度约为19.2 m.
解:在Rt△ABD中,
∵∠ABD=30°,AB=10 m,
∴AD=AB·sin∠ABD=10×sin30°=5(m).
∴AC=ADsin∠ACD=5sin15°≈50.26≈19.2(m).
1.三角函数的计算方法:
2.特殊角的三角函数值:
我们把斜坡与水平面的夹角α称为坡角.
斜坡的垂直高度BC (h) 与斜坡的水平距离AC (l)的比称为坡度 (或坡比),记作i,即 i = h : l .
【分析】作梯形ABCD的高CE、DF.根据题意,在Rt△AFD和Rt△BEC中,可以分别求出AF与BE的长,从而可求得坝底AB的长.
解:如图,作CE⊥AB,DF⊥AB,垂足分别为E、F.
用计算器计算,得β ≈ 39. 8.
(2)在Rt△BEC中,α = 30°,∠BCE= 90°-30°= 60°, EB = CE·tan∠BCE = 4.5× tan 60°.
∴AF= 1.2DF = 1.2×4.5= 5.4.
又FE= DC= 2.5,
∴AB = AF+FE+EB= 5.4+2.5+4.5×tan60°≈15.7.
我们在观察物体时,视线与水平线所成的角称为仰角或俯角.
从上往下看,视线与水平线的夹角叫做俯角.
右图中的∠1就是________, ∠2就是________.
从下往上看,视线与水平线的夹角叫仰角.
解:如图,α = 30°,β= 60°, AD=120.
∴BD=AD· tana =120· tan30°
CD=AD· tanβ =120· tan60°
因此,这栋楼高约为277.1m.
解:如图 ,在Rt△APC中,
PC=PA·cs(90°-65°)
=80×cs25°≈80×0.91=72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130n mile.
用锐角三角函数解决实际问题
【分析】如图,用⊙O表示摩天轮,小明从底部点A出发,经过2 min后到达点B,由题意可求∠BOA的大小.如果作BC⊥OA,垂足为C,在Rt△OCB中,可以根据OB及∠BOA的大小求得OC,那么就可知道此时小明离地面的高度.
解:如图,用⊙O表示摩天轮,A、B分别表示小明的出发点和2 min后的到达点.由题意知,OB= 20,∠BOA = 360°÷6= 60°.作BC⊥OA,垂足为C.在Rt△OCB中,
答:2 min后小明离地面10. 3 m.
AC = AO-CO= 20-10= 10.因为摩天轮底部与地面相距0.3 m,所以小明离地面的高度应为10.3 m.
2.小亮为测量如图所示的湖面的宽度BC,他在同一水平面上取一点A,测得湖的一端C在A处的正北方向,另一端B在A处的北偏东60°的方向,并测得A,C间的距离AC=10 m,则湖的宽度BC为________m.
3.某水库堤坝的横断面如图所示,迎水坡AB的坡度是1∶3,堤坝高BC=50 m,则AB=_______m.
5.某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯. 如图,已知原阶梯式自动扶梯AB长为10 m,坡角∠ABD=30°,改造后的斜坡式自动扶梯的坡角∠ACB=15°,请你计算改造后的斜坡式自动扶梯AC的长度.(结果精确到0.1 m,参考数据:sin15°≈0.26,cs15°≈0.97,tan15°≈0.27)
答:改造后的斜坡式自动扶梯AC的长度约为19.2 m.
解:在Rt△ABD中,
∵∠ABD=30°,AB=10 m,
∴AD=AB·sin∠ABD=10×sin30°=5(m).
∴AC=ADsin∠ACD=5sin15°≈50.26≈19.2(m).













