湖南省长沙市雅礼中学2022-2023学年高二上学期期中数学试题及参考答案

雅礼教育集团2022年下学期期中考试试卷高二数学

一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 设集合，，则（    ）

A.  B.  C.  D.

【答案】B

【解析】

【分析】利用交集的定义可求.

【详解】由题设有，

故选：B .

2. 已知复数z满足（i为虚数单位），则（    ）

A.  B.  C. 1 D. 2

【答案】B

【解析】

【分析】根据复数模的性质运算即可.

【详解】,

,

．

故选：B

3. 已知点，向量，则向量（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】根据平面向量加法的坐标运算可得答案.

【详解】，.

故选：C.

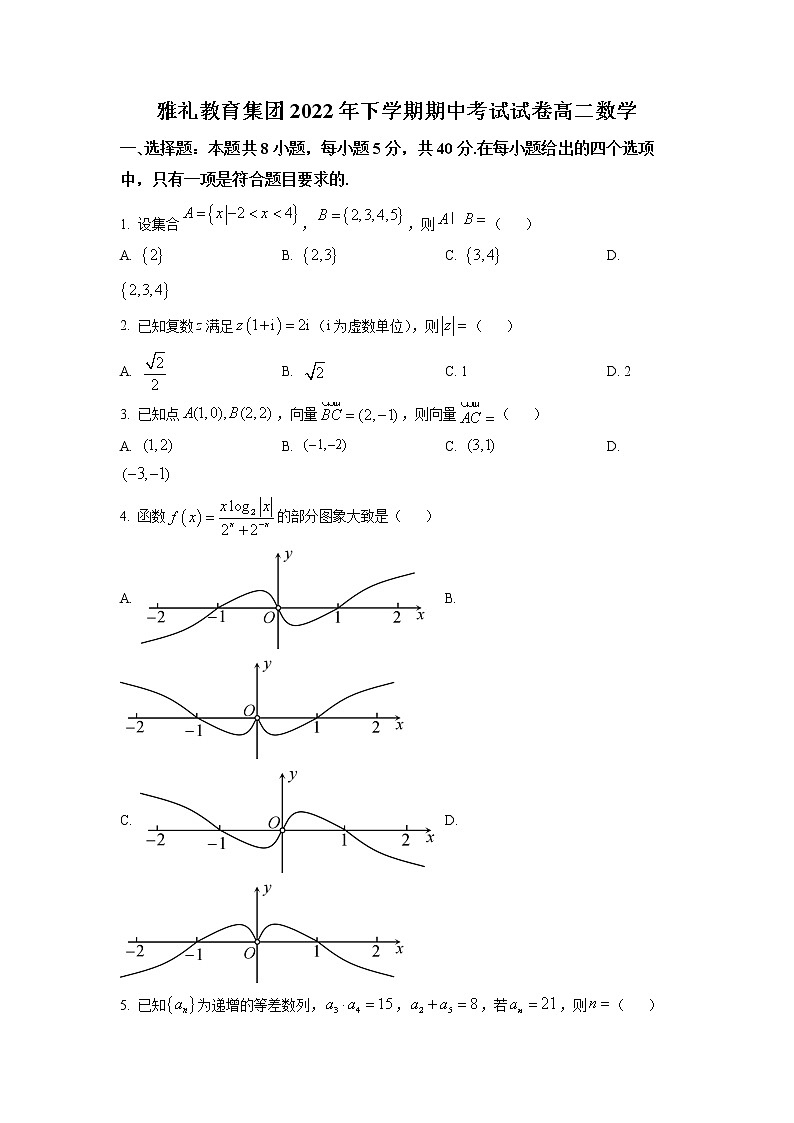
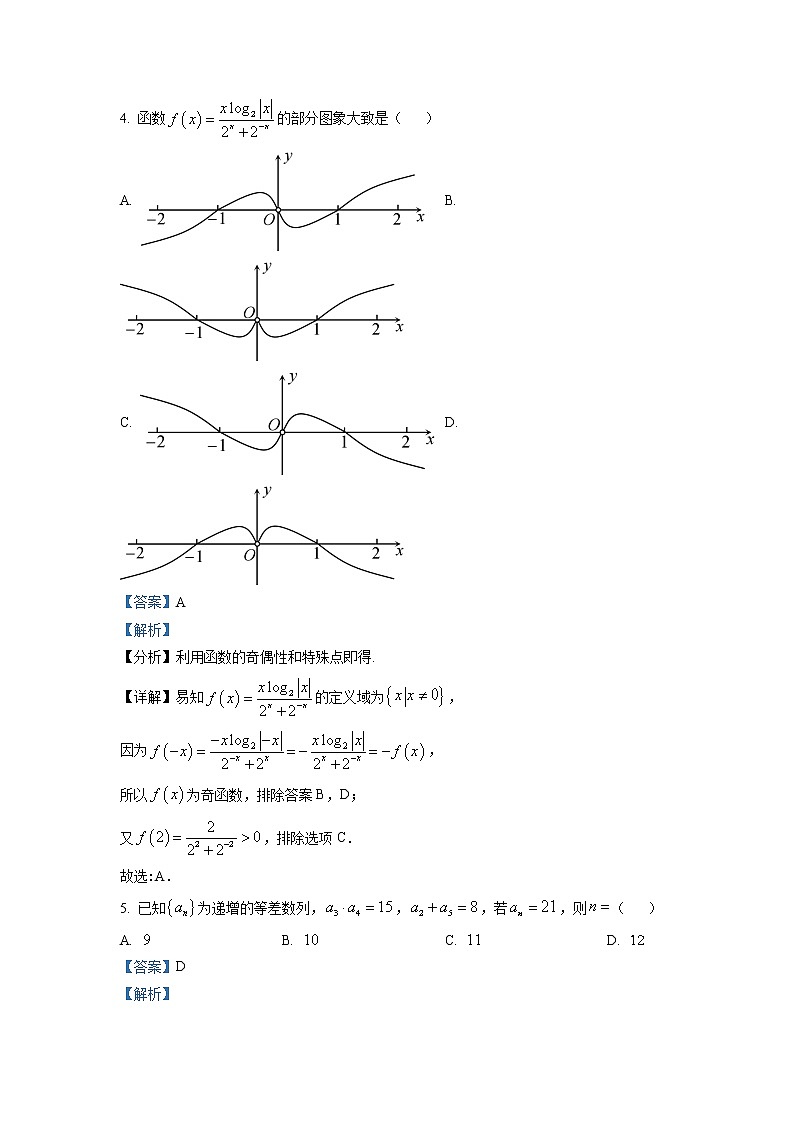
4. 函数的部分图象大致是（    ）

A.  B.

C.  D.

【答案】A

【解析】

【分析】利用函数的奇偶性和特殊点即得.

【详解】易知的定义域为，

因为，

所以为奇函数，排除答案B，D；

又，排除选项C．

故选:A．

5. 已知为递增的等差数列，，，若，则（    ）

A.  B.  C.  D.

【答案】D

【解析】

【分析】根据等差数列的性质列出方程组，从而求出和公差，写出的通项公式即可求出答案.

【详解】因为为等差数列，，所以，

由，得或(舍)，所以，

所以.

令，得.

故选：D.

6. 若在区间上单调递增，则实数a的最大值为（    ）

A  B.  C.  D. π

【答案】A

【解析】

【分析】先求出函数增区间，进而建立不等式组解得答案即可.

【详解】易知将函数的图象向右平移得到函数的图象，则函数的增区间为，而函数又在上单调递增，所以，于是，即a的最大值为.

故选：A.

7. 过抛物线的焦点且斜率为1的直线与该拋物线交于两点，则线段的中点到准线的距离为（    ）

A. 3 B. 4 C. 5 D. 6

【答案】B

【解析】

【分析】根据抛物线方程求出焦点坐标和准线，然后根据过焦点直线方程和抛物线联立求得线段中点横坐标即可求得答案.

【详解】解：由题意得：

的交点坐标为，准线为

直线，设

联立直线和双曲线方程可知：

有韦达定理可知：

线段的中点横坐标为：

故线段的中点到准线的距离为

故选：B

8. 中国的5G技术领先世界，5G技术的数学原理之一便是著名的香农公式：.它表示，在受噪音干扰的信道中，最大信息传递速度C取决于信道带宽W，信道内信号的平均功率S，信道内部的高斯噪声功率N的大小，其中叫作信噪比.当信噪比比较大时，公式中真数里面的1可以忽略不计.按照香农公式，增加带宽，提高信号功率和降低噪声功率都可以提升信息传递速度，若在信噪比为1000的基础上，将带宽W增大到原来的2倍，信号功率S增大到原来的10倍，噪声功率N减小到原来的，则信息传递速度C大约增加了（    ）（参考数据：）

A. 87% B. 123% C. 156% D. 213%

【答案】D

【解析】

【分析】先求得提升前的信息传递速度，然后求得提升后的信息传播速度，由此求得正确答案.

【详解】提升前的信息传递速度，

提升后的信息传递速度，

所以信息传递速度C大约增加了.

故选：D

二､多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 一箱产品有正品10件，次品2件，从中任取2件，有如下事件，其中互斥事件有（    ）

A. “恰有1件次品”和“恰有2件次品” B.

C. “至少有1件正品”和“至少有1件次品” D. “至少有1件次品”和“都是正品”

【答案】AD

【解析】

【分析】判断各选项中的事件是否有同时发生的可能，即可确定答案.

【详解】A：“恰有1件次品”和“恰有2件次品”不可能同时发生，为互斥事件；

B：“都是次品”的基本事件中包含了“至少有1件次品”的事件，不是互斥事件；

C：“至少有1件正品” 的基本事件为{“有1件正品和1件次品” ，“有2件正品” }，“至少有1件次品” 的基本事件为{“有1件正品和1件次品” ，“有2件次品” }，它们有共同的基本事件“有1件正品和1件次品” ，不是互斥事件；

D：由C分析知：“至少有1件次品”和“都是正品”不可能同时发生，为互斥事件；

故选：AD

10. 已知圆，一条光线从点射出经轴反射，下列结论正确的是（    ）

A. 圆关于轴的对称圆的方程为

B. 若反射光线平分圆的周长，则入射光线所在直线方程为

C. 若反射光线与圆相切于，与轴相交于点，则.

D. 若是圆上的任意一点，则的最大值为

【答案】AB

【解析】

【分析】由点关于直线的对称，直线与圆的位置关系，圆的性质对选项逐一判断，

【详解】圆的方程为，圆心，半径为1，

对于A，关于轴的对称点为，圆关于轴的对称圆为，化简得，故A正确，

对于B，若反射光线平分圆的周长，即反射光线过圆心，入射光线延长线过，

可得入射光线所在直线方程为，故B正确，

对于C，若反射光线与圆相切，则入射光线延长线与圆相切于点，

到的距离为，由对称性得，故C错误，

对于D，到圆心的距离为，由圆的性质得的最大值为，故D错误，

故选：AB

11. 已知a，，，且，则下列说法正确的为（    ）

A. ab的最小值为1 B.

C.  D.

【答案】BC

【解析】

【分析】直接根据基本不等式判断各选项的对错即可.

【详解】因为，由基本不等式可得，当且仅当时等号成立，

又，所以，当且仅当时等号成立，故ab的最大值为1，A错，

，当且仅当时等号成立，B对，

，当且仅当时等号成立，C对，

，当且仅当，时等号成立，D错，

故选：BC.

12. 如图，已知A，B是相互垂直的两条异面直线，直线AB与a，b均相互垂直，垂足分别为A，B，且，动点P，Q分别位于直线A，B上，且P异于A，Q异于B.若直线PQ与AB所成的角，线段PQ的中点为M，下列说法正确的是（    ）

A. PQ的长度为定值

B. 三棱锥的外接球的半径长为定值

C. 三棱锥体积为定值

D. 点M到AB的距离为定值

【答案】ABD

【解析】

【分析】根据题意，将图形还原为长方体，进而根据题意求出，进而判断A，B；

根据，进而判断C；

设交于R，则R为CQ的中点，取AB的中点N，然后证明四边形RBNM是平行四边形，进而证明，最后求得答案.

【详解】如图，将图形还原为长方体，

因为，所以（易知其为锐角）是PQ与AB所成的角，即，易知，则.A正确；

对B，易知三棱锥的外接球与长方体的外接球相同，则其直径为4，半径为2.B正确；

对C，

，不为定值.C错误；

对D，设交于R，则R为CQ的中点，连接MR，取AB的中点N，连接MN，又因为M为PQ的中点，所以，而，故，所以四边形RBNM是平行四边形，则，因为，则.

因为AB⊥平面BCDQ，平面BCDQ，所以，则，所以点M到AB的距离为1.D正确.

故选：ABD.

三､填空题：本题共4小题，每小题5分，共20分.

13. 若直线与互相垂直，则实数___________．

【答案】

【解析】

【分析】根据两直线位置关系直接可得参数值.

【详解】由，即，

又直线与直线互相垂直，

故，

解得，

故答案为：.

14. 已知甲､乙两球落入盒子的概率分别为和.假定两球是否落入盒子互不影响，则甲､乙两球恰好有一个落入盒子的概率为___________.

【答案】##

【解析】

【分析】设甲球落入盒子为事件A，乙球落入盒子为事件B，求出即得解.

【详解】设甲球落入盒子为事件A，乙球落入盒子为事件B，

则甲､乙两球恰好有一个落入盒子为,

所以.

故答案为：

15. 函数的值域是___________，最小正周期是___________.

【答案】    ①.     ②.

【解析】

【分析】根据分段函数画出图像即可知道值域和周期.

【详解】解：由题意得：

如图所示：

故函数的值域为：，最小正周期为

故答案为：；

16. 已知椭圆的右焦点为上的两点关于原点对称，，且，则离心率的取值范围是___________.

【答案】

【解析】

【分析】设椭圆的左焦点为E，根据椭圆的定义可知，，利用余弦定理求出，利用，最后结合平面向量的数量积计算即可得答案.

【详解】解：由题意得：

椭圆的左焦点为E，则

因为两点关于原点对称，所以四边形为平行四边形

由，得，，且

在中，

，

由得：

整理得：，又

所以

故答案为:

四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.

17. 已知圆C的圆心为点，且与坐标轴相切.

（1）求圆C的方程；

（2）求直线被圆C所截得的弦长.

【答案】（1）   

（2）

【解析】

【分析】（1）由圆心与坐标轴相切确定半径长度，即可直接写出方程；

（2）先用点线距离公式求出圆心C到直线l的距离，结合垂径定理即可求弦长；

【小问1详解】

∵圆C的圆心为点，且与坐标轴相切，

∴圆C的半径为，

∴圆C的方程为.

【小问2详解】

∵圆C的圆心，

∴圆心C到直线l的距离为.

∴所求的弦长为.

18. △ABC的内角A，B，C的对边分别是a，b，c，且．

（1）求B；

（2）若△ABC的面积为，且，求△ABC的周长．

【答案】（1）   

（2）

【解析】

【分析】（1）先对已知等式利用正弦定理统一成边的形式，化简后再利用余弦定理可求出角，

（2）由三角形的面积可求出，再利用余弦定理结合已知条件可求出和的值.

【小问1详解】

因为，

所以由正弦定理得，

展开得，所以，

因为，所以．

【小问2详解】

由（1）知，解得，

因为，

由余弦定理得，

即，解得，，

所以△ABC的周长为．

19. 如图所示，已知椭圆的上顶点为，左､右焦点分别为为正三角形.过且垂直于的直线与交于两点，.

（1）求椭圆的离心率；

（2）求四边形的面积.

【答案】（1）   

（2）

【解析】

【分析】(1)根据图象可知：，因为为正三角形，进而得出的关系即可求解；

(2)根据（1）将椭圆方程可化为，设出直线的方程，与椭圆方程联立，利用两点间距离公式求出的值，进而求出四边形的面积.

【小问1详解】

由图可知：，

因为为正三角形，所以，也即，

所以，所以椭圆的离心率为.

【小问2详解】

由（1）可知：，所以，

椭圆方程可化为：，直线的斜率为，

因为直线垂直于，所以，又因为直线过点,

所以直线的方程为：，设，

联立方程组：，整理可得：，

所以，

所以，

因为，所以，解得：，

所以四边形的面积.

20. 已知数列的前项和为.

（1）证明：.

（2）求数列的通项公式.

【答案】（1）证明见解析；   

（2）

【解析】

【分析】（1）由，可得当时，两式相减即可求证；

（2）由（1）数列的奇数项与偶数项分别为等差数列，进而可求得通项公式.

【小问1详解】

证明：

当时，，

 又，故可知

所以

【小问2详解】

解：由题意得：

当时，，又因为，故可知

由，可知数列的奇数项与偶数项分别为等差数列，公差为，首项分别为：1，3

当时，

当时，

21. 如图，四棱台中，上底面是边长为1的菱形，下底面ABCD是边长为2的菱形，平面ABCD且

（1）求证：平面平面；

（2）若直线AB与平面所成角的正弦为，求棱台的体积．

【答案】（1）证明见解析   

（2）

【解析】

【分析】（1）根据题意利用线面垂直的定义与判定可证平面；（2）利用空间向量，根据线面夹角可得，利用台体体积公式计算求解．

【小问1详解】

∵菱形ABCD对角线相互垂直，

∴

∵平面ABCD，平面ABCD，

∴

∵，平面，平面

∴平面

∵平面

∴平面平面

【小问2详解】

设，则且

∴且，

∴平面ABCD

以O为原点，OA、OB、所在的直线为坐标轴，建立直角坐标系，如图，

则，设，

则

，，，

设平面的一个法向量

则可得，

取，得

由题

整理得，则

∴，

∴

22. 在平面直角坐标系中，双曲线的离心率为，实轴长为4.

（1）求C方程；

（2）如图，点A为双曲线的下顶点，直线l过点且垂直于y轴（P位于原点与上顶点之间），过P的直线交C于G，H两点，直线AG，AH分别与l交于M，N两点，若O，A，N，M四点共圆，求点P的坐标.

【答案】（1）   

（2）

【解析】

【分析】（1）根据双曲线的离心率结合实轴长，可求得a,b,即得答案;

（2）根据O，A，N，M四点共圆结合几何性质可推出，设，，，从而可以用点的坐标表示出t,再设直线，联立双曲线与直线方程，利用根与系数的关系式，代入t的表达式中化简，可得答案.

【小问1详解】

因为实轴长为4，即，，

又，所以，，

故C的方程为.

【小问2详解】

由O，A，N，M四点共圆可知，，

又，即，

故，

即，所以,

设，，，

由题意可知，则直线，直线，

因为M在直线l上，所以，代入直线AG方程，可知，

故M坐标为，所以，

又，由，则，

整理可得，

当直线GH斜率不存在时，显然不符合题意，

故设直线，代入双曲线方程：中，

可得，所以，，

又

，

所以,

故，即，所以点P坐标.

【点睛】本题考查了双曲线方程的求解，以及直线和双曲线的位置关系的问题，解答时要注意明确点线的位置关系，能设相关点的坐标，从而表示出参数的表达式，再结合联立直线和双曲线方程，利用根与系数的关系式化简，难点在于较为繁杂的计算，要十分细心.